Q-S5: Towards Quantized State Space Models

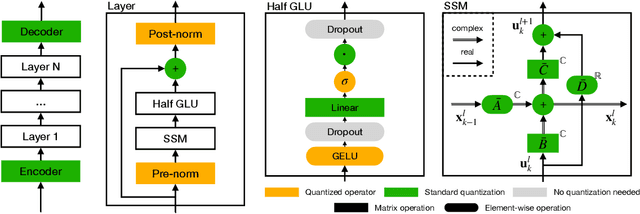
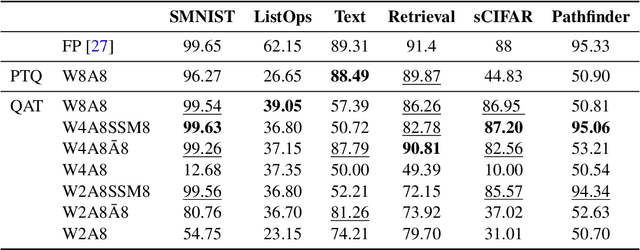
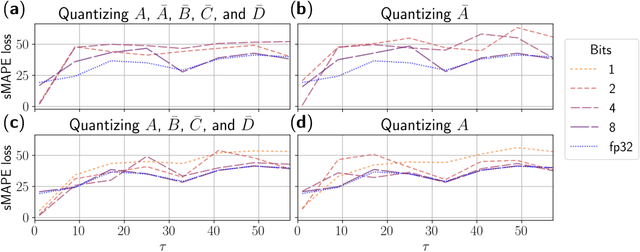
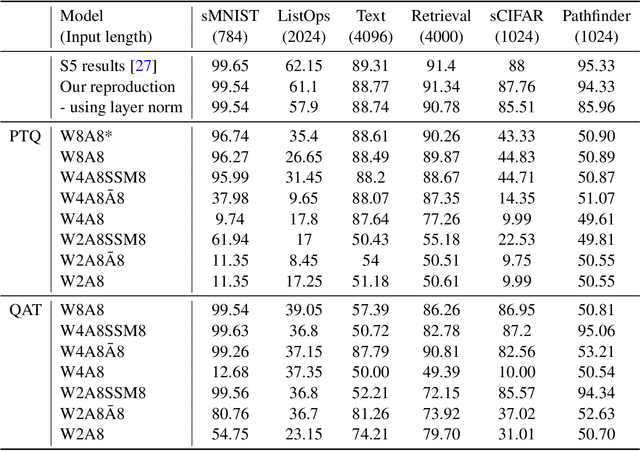
In the quest for next-generation sequence modeling architectures, State Space Models (SSMs) have emerged as a potent alternative to transformers, particularly for their computational efficiency and suitability for dynamical systems. This paper investigates the effect of quantization on the S5 model to understand its impact on model performance and to facilitate its deployment to edge and resource-constrained platforms. Using quantization-aware training (QAT) and post-training quantization (PTQ), we systematically evaluate the quantization sensitivity of SSMs across different tasks like dynamical systems modeling, Sequential MNIST (sMNIST) and most of the Long Range Arena (LRA). We present fully quantized S5 models whose test accuracy drops less than 1% on sMNIST and most of the LRA. We find that performance on most tasks degrades significantly for recurrent weights below 8-bit precision, but that other components can be compressed further without significant loss of performance. Our results further show that PTQ only performs well on language-based LRA tasks whereas all others require QAT. Our investigation provides necessary insights for the continued development of efficient and hardware-optimized SSMs.

Neuromorphic Intermediate Representation: A Unified Instruction Set for Interoperable Brain-Inspired Computing

Spiking neural networks and neuromorphic hardware platforms that emulate neural dynamics are slowly gaining momentum and entering main-stream usage. Despite a well-established mathematical foundation for neural dynamics, the implementation details vary greatly across different platforms. Correspondingly, there are a plethora of software and hardware implementations with their own unique technology stacks. Consequently, neuromorphic systems typically diverge from the expected computational model, which challenges the reproducibility and reliability across platforms. Additionally, most neuromorphic hardware is limited by its access via a single software frameworks with a limited set of training procedures. Here, we establish a common reference-frame for computations in neuromorphic systems, dubbed the Neuromorphic Intermediate Representation (NIR). NIR defines a set of computational primitives as idealized continuous-time hybrid systems that can be composed into graphs and mapped to and from various neuromorphic technology stacks. By abstracting away assumptions around discretization and hardware constraints, NIR faithfully captures the fundamental computation, while simultaneously exposing the exact differences between the evaluated implementation and the idealized mathematical formalism. We reproduce three NIR graphs across 7 neuromorphic simulators and 4 hardware platforms, demonstrating support for an unprecedented number of neuromorphic systems. With NIR, we decouple the evolution of neuromorphic hardware and software, ultimately increasing the interoperability between platforms and improving accessibility to neuromorphic technologies. We believe that NIR is an important step towards the continued study of brain-inspired hardware and bottom-up approaches aimed at an improved understanding of the computational underpinnings of nervous systems.

Subspace tracking for independent phase noise source separation in frequency combs

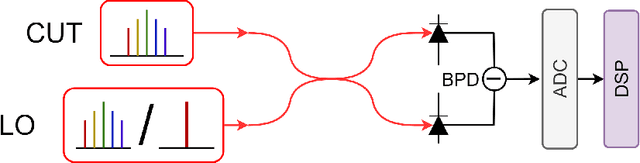
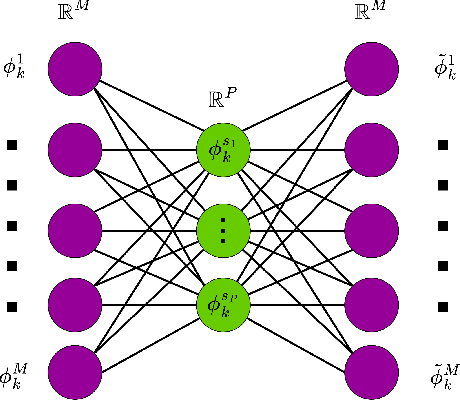
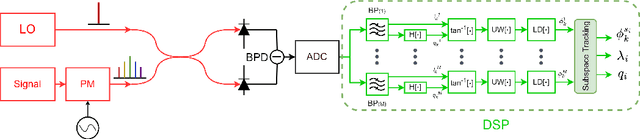
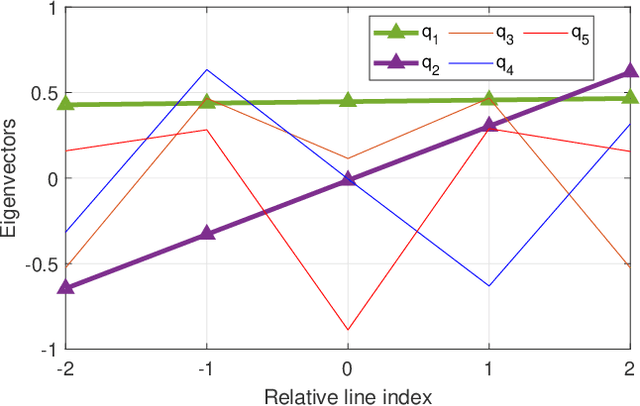
Advanced digital signal processing techniques in combination with ultra-wideband balanced coherent detection have enabled a new generation of ultra-high speed fiber-optic communication systems, by moving most of the processing functionalities into digital domain. In this paper, we demonstrate how digital signal processing techniques, in combination with ultra-wideband balanced coherent detection can enable optical frequency comb noise characterization techniques with novel functionalities. We propose a measurement method based on subspace tracking, in combination with multi-heterodyne coherent detection, for independent phase noise sources identification, separation and measurement. Our proposed measurement technique offers several benefits. First, it enables the separation of the total phase noise associated with a particular comb-line or -lines into multiple independent phase noise terms associated with different noise sources. Second, it facilitates the determination of the scaling of each independent phase noise term with comb-line number. Our measurement technique can be used to: identify the most dominant source of phase noise; gain a better understanding of the physics behind the phase noise accumulation process; and confirm, already existing, and enable better phase noise models. In general, our measurement technique provides new insights into noise behavior of optical frequency combs.