An Analysis Of Entire Space Multi-Task Models For Post-Click Conversion Prediction

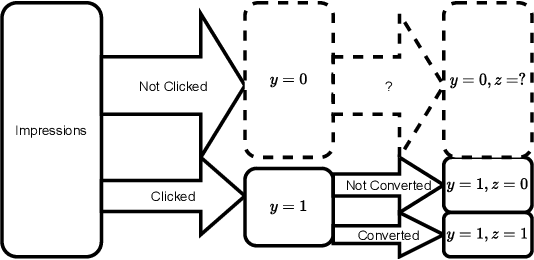
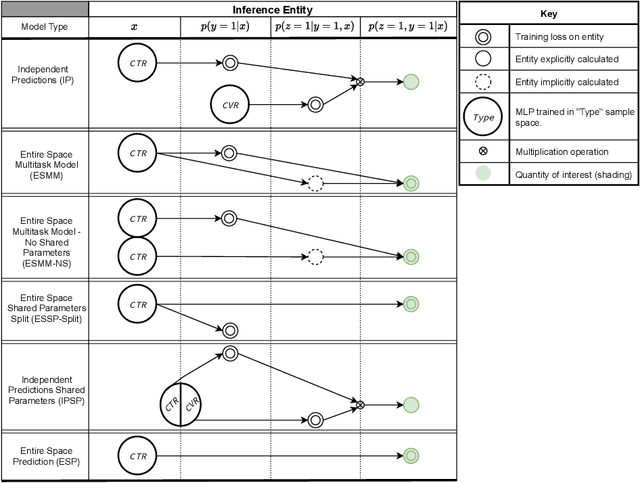
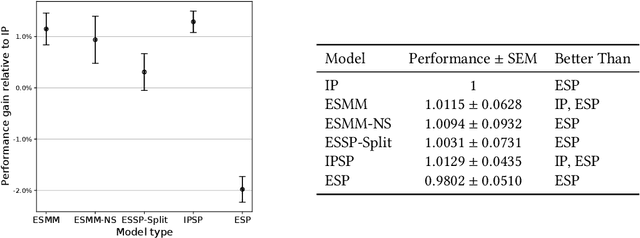
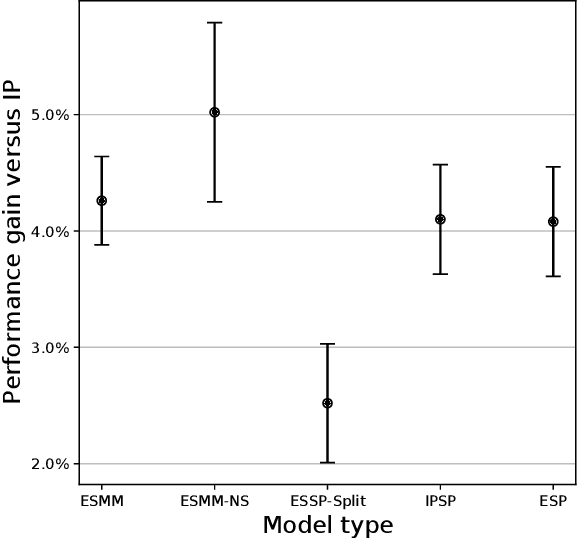
Industrial recommender systems are frequently tasked with approximating probabilities for multiple, often closely related, user actions. For example, predicting if a user will click on an advertisement and if they will then purchase the advertised product. The conceptual similarity between these tasks has promoted the use of multi-task learning: a class of algorithms that aim to bring positive inductive transfer from related tasks. Here, we empirically evaluate multi-task learning approaches with neural networks for an online advertising task. Specifically, we consider approximating the probability of post-click conversion events (installs) (CVR) for mobile app advertising on a large-scale advertising platform, using the related click events (CTR) as an auxiliary task. We use an ablation approach to systematically study recent approaches that incorporate both multitask learning and "entire space modeling" which train the CVR on all logged examples rather than learning a conditional likelihood of conversion given clicked. Based on these results we show that several different approaches result in similar levels of positive transfer from the data-abundant CTR task to the CVR task and offer some insight into how the multi-task design choices address the two primary problems affecting the CVR task: data sparsity and data bias. Our findings add to the growing body of evidence suggesting that standard multi-task learning is a sensible approach to modelling related events in real-world large-scale applications and suggest the specific multitask approach can be guided by ease of implementation in an existing system.

Adaptive Monte Carlo via Bandit Allocation

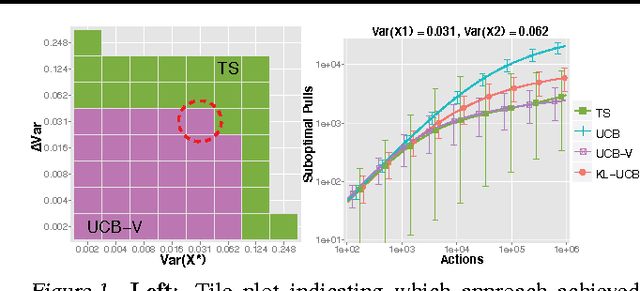
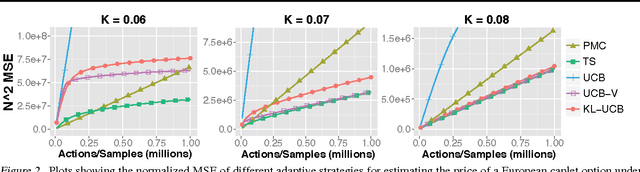
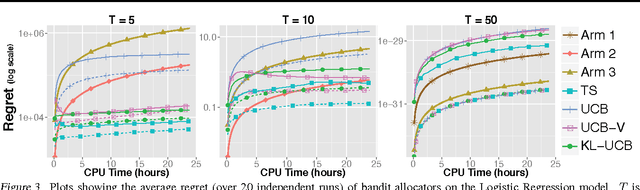
We consider the problem of sequentially choosing between a set of unbiased Monte Carlo estimators to minimize the mean-squared-error (MSE) of a final combined estimate. By reducing this task to a stochastic multi-armed bandit problem, we show that well developed allocation strategies can be used to achieve an MSE that approaches that of the best estimator chosen in retrospect. We then extend these developments to a scenario where alternative estimators have different, possibly stochastic costs. The outcome is a new set of adaptive Monte Carlo strategies that provide stronger guarantees than previous approaches while offering practical advantages.

Regularizers versus Losses for Nonlinear Dimensionality Reduction: A Factored View with New Convex Relaxations

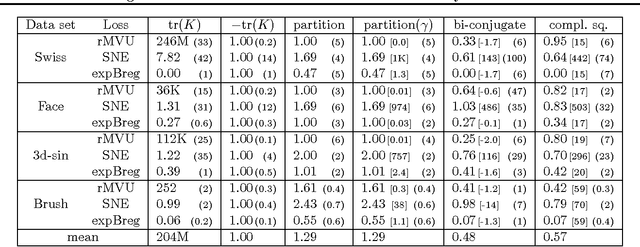
We demonstrate that almost all non-parametric dimensionality reduction methods can be expressed by a simple procedure: regularized loss minimization plus singular value truncation. By distinguishing the role of the loss and regularizer in such a process, we recover a factored perspective that reveals some gaps in the current literature. Beyond identifying a useful new loss for manifold unfolding, a key contribution is to derive new convex regularizers that combine distance maximization with rank reduction. These regularizers can be applied to any loss.