An Analysis of SVD for Deep Rotation Estimation

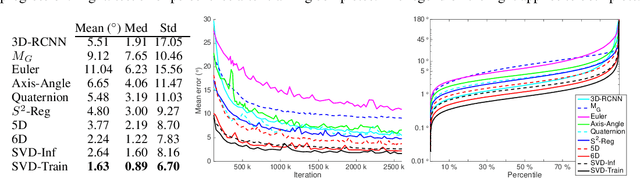
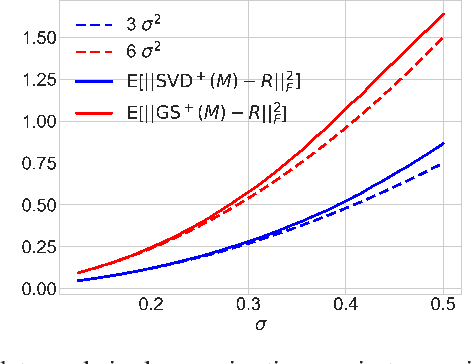
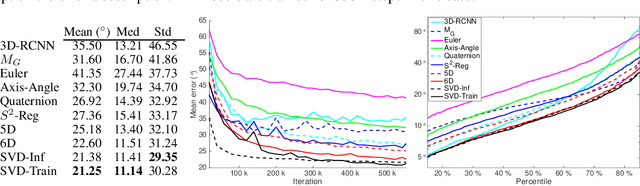
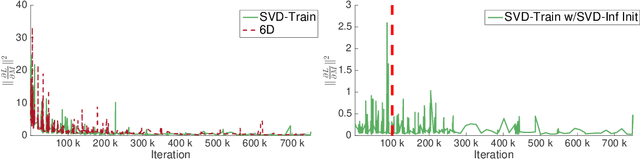
Symmetric orthogonalization via SVD, and closely related procedures, are well-known techniques for projecting matrices onto $O(n)$ or $SO(n)$. These tools have long been used for applications in computer vision, for example optimal 3D alignment problems solved by orthogonal Procrustes, rotation averaging, or Essential matrix decomposition. Despite its utility in different settings, SVD orthogonalization as a procedure for producing rotation matrices is typically overlooked in deep learning models, where the preferences tend toward classic representations like unit quaternions, Euler angles, and axis-angle, or more recently-introduced methods. Despite the importance of 3D rotations in computer vision and robotics, a single universally effective representation is still missing. Here, we explore the viability of SVD orthogonalization for 3D rotations in neural networks. We present a theoretical analysis that shows SVD is the natural choice for projecting onto the rotation group. Our extensive quantitative analysis shows simply replacing existing representations with the SVD orthogonalization procedure obtains state of the art performance in many deep learning applications covering both supervised and unsupervised training.

A Random Matrix Perspective on Mixtures of Nonlinearities for Deep Learning

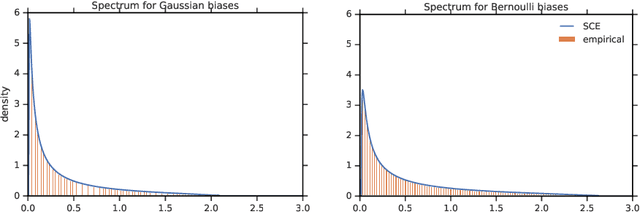
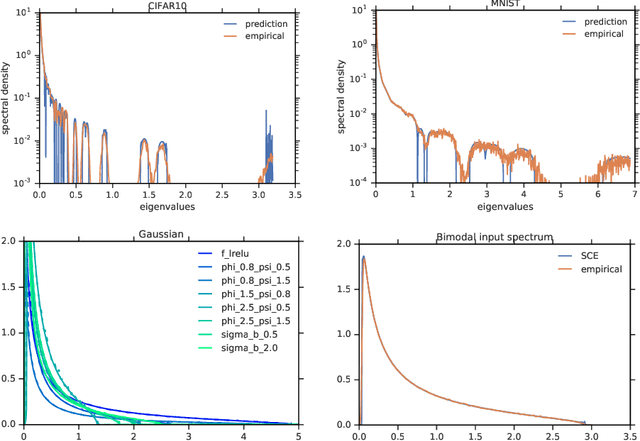
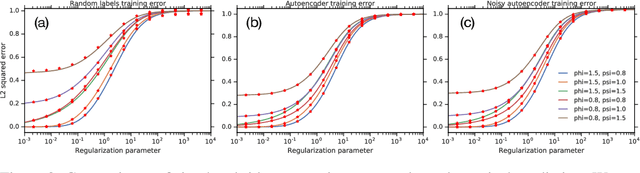
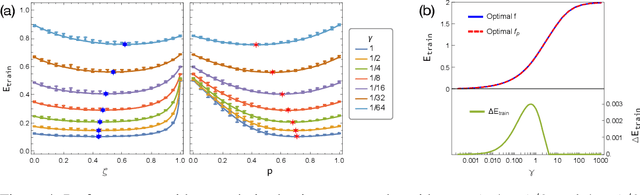
One of the distinguishing characteristics of modern deep learning systems is that they typically employ neural network architectures that utilize enormous numbers of parameters, often in the millions and sometimes even in the billions. While this paradigm has inspired significant research on the properties of large networks, relatively little work has been devoted to the fact that these networks are often used to model large complex datasets, which may themselves contain millions or even billions of constraints. In this work, we focus on this high-dimensional regime in which both the dataset size and the number of features tend to infinity. We analyze the performance of a simple regression model trained on the random features $F=f(WX+B)$ for a random weight matrix $W$ and random bias vector $B$, obtaining an exact formula for the asymptotic training error on a noisy autoencoding task. The role of the bias can be understood as parameterizing a distribution over activation functions, and our analysis directly generalizes to such distributions, even those not expressible with a traditional additive bias. Intriguingly, we find that a mixture of nonlinearities can outperform the best single nonlinearity on the noisy autoecndoing task, suggesting that mixtures of nonlinearities might be useful for approximate kernel methods or neural network architecture design.

Latent feature disentanglement for 3D meshes

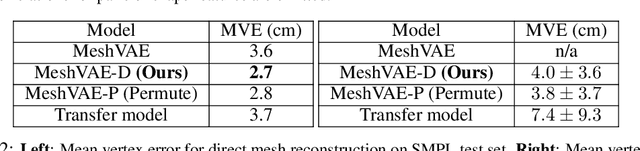
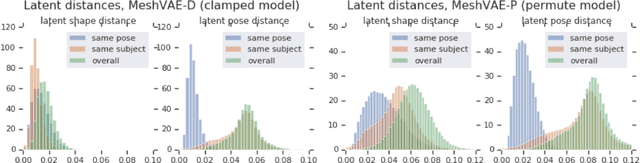
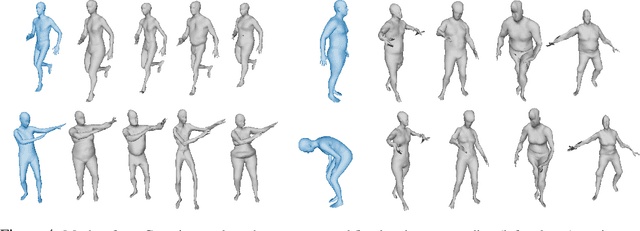
Generative modeling of 3D shapes has become an important problem due to its relevance to many applications across Computer Vision, Graphics, and VR. In this paper we build upon recently introduced 3D mesh-convolutional Variational AutoEncoders which have shown great promise for learning rich representations of deformable 3D shapes. We introduce a supervised generative 3D mesh model that disentangles the latent shape representation into independent generative factors. Our extensive experimental analysis shows that learning an explicitly disentangled representation can both improve random shape generation as well as successfully address downstream tasks such as pose and shape transfer, shape-invariant temporal synchronization, and pose-invariant shape matching.