Meta-Learning Deep Energy-Based Memory Models

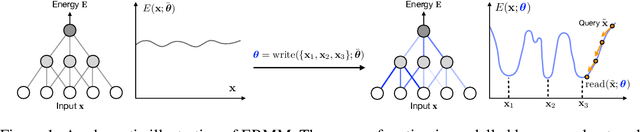
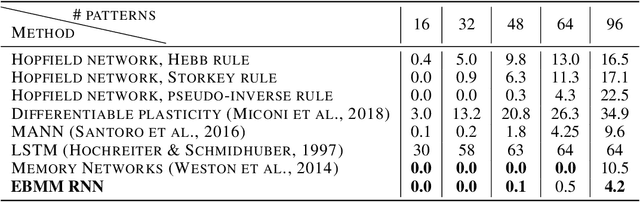
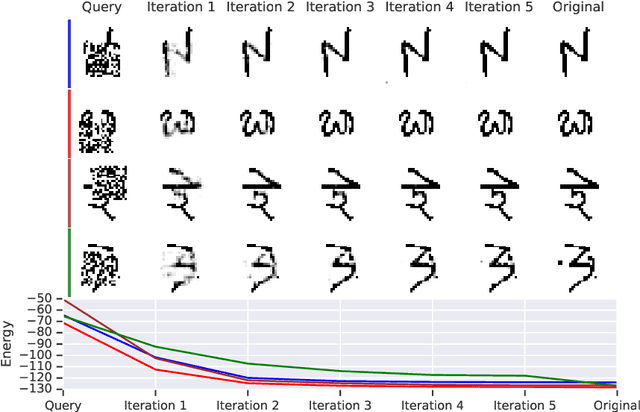
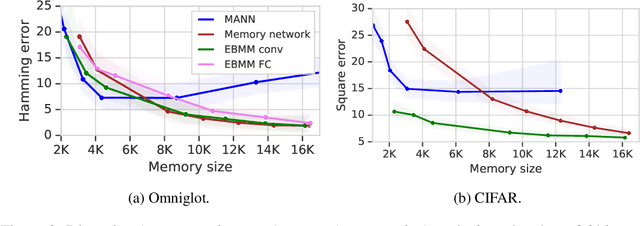
We study the problem of learning associative memory -- a system which is able to retrieve a remembered pattern based on its distorted or incomplete version. Attractor networks provide a sound model of associative memory: patterns are stored as attractors of the network dynamics and associative retrieval is performed by running the dynamics starting from a query pattern until it converges to an attractor. In such models the dynamics are often implemented as an optimization procedure that minimizes an energy function, such as in the classical Hopfield network. In general it is difficult to derive a writing rule for a given dynamics and energy that is both compressive and fast. Thus, most research in energy-based memory has been limited either to tractable energy models not expressive enough to handle complex high-dimensional objects such as natural images, or to models that do not offer fast writing. We present a novel meta-learning approach to energy-based memory models (EBMM) that allows one to use an arbitrary neural architecture as an energy model and quickly store patterns in its weights. We demonstrate experimentally that our EBMM approach can build compressed memories for synthetic and natural data, and is capable of associative retrieval that outperforms existing memory systems in terms of the reconstruction error and compression rate.

Meta-Learning Neural Bloom Filters

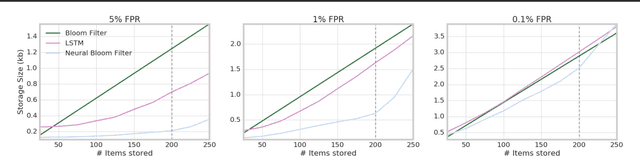
There has been a recent trend in training neural networks to replace data structures that have been crafted by hand, with an aim for faster execution, better accuracy, or greater compression. In this setting, a neural data structure is instantiated by training a network over many epochs of its inputs until convergence. In applications where inputs arrive at high throughput, or are ephemeral, training a network from scratch is not practical. This motivates the need for few-shot neural data structures. In this paper we explore the learning of approximate set membership over a set of data in one-shot via meta-learning. We propose a novel memory architecture, the Neural Bloom Filter, which is able to achieve significant compression gains over classical Bloom Filters and existing memory-augmented neural networks.

Fast Parametric Learning with Activation Memorization

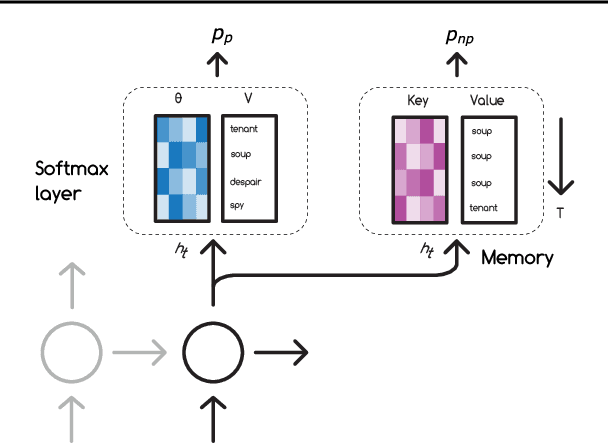
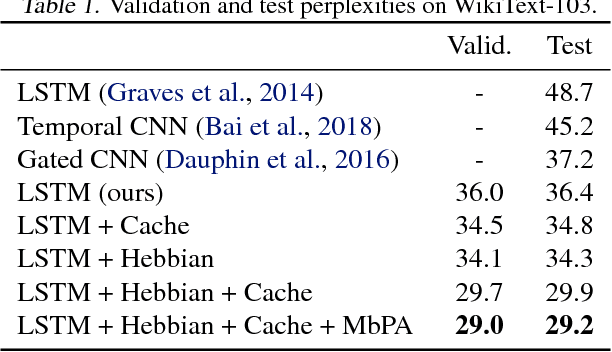
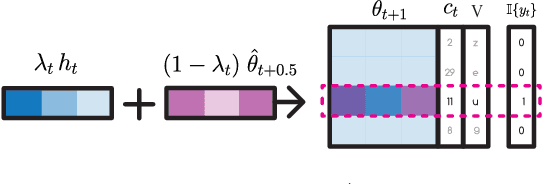
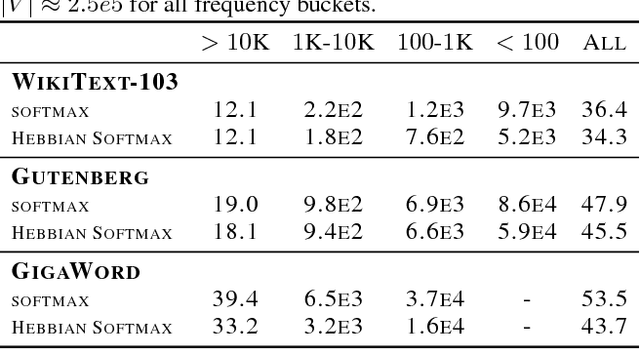
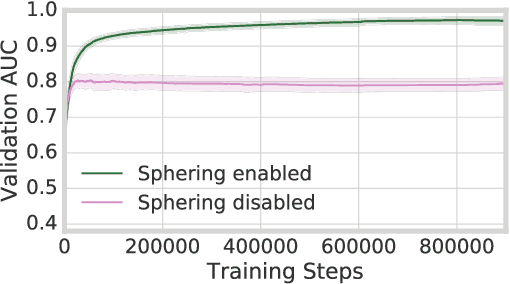
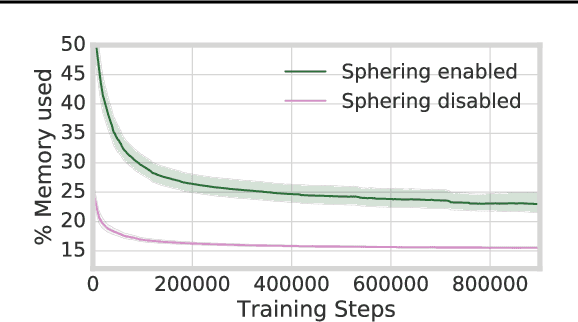
Neural networks trained with backpropagation often struggle to identify classes that have been observed a small number of times. In applications where most class labels are rare, such as language modelling, this can become a performance bottleneck. One potential remedy is to augment the network with a fast-learning non-parametric model which stores recent activations and class labels into an external memory. We explore a simplified architecture where we treat a subset of the model parameters as fast memory stores. This can help retain information over longer time intervals than a traditional memory, and does not require additional space or compute. In the case of image classification, we display faster binding of novel classes on an Omniglot image curriculum task. We also show improved performance for word-based language models on news reports (GigaWord), books (Project Gutenberg) and Wikipedia articles (WikiText-103) --- the latter achieving a state-of-the-art perplexity of 29.2.

Scaling Memory-Augmented Neural Networks with Sparse Reads and Writes

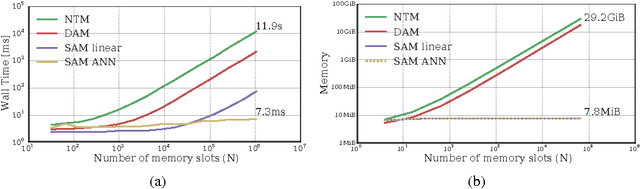
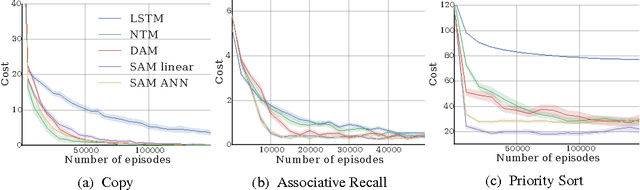
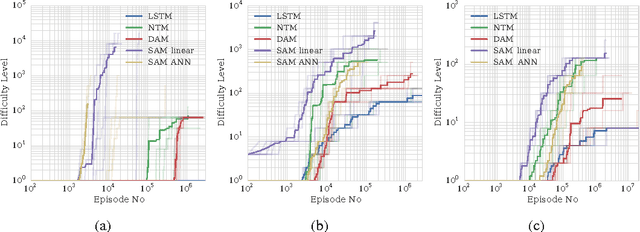
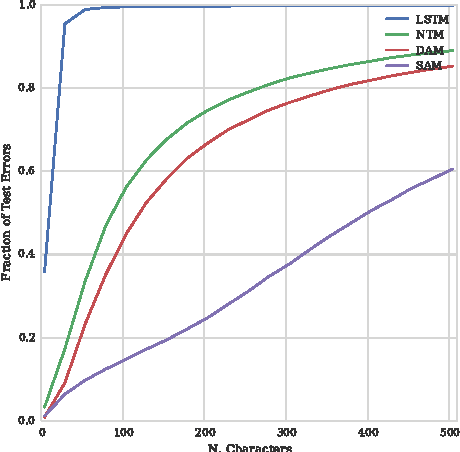
Neural networks augmented with external memory have the ability to learn algorithmic solutions to complex tasks. These models appear promising for applications such as language modeling and machine translation. However, they scale poorly in both space and time as the amount of memory grows --- limiting their applicability to real-world domains. Here, we present an end-to-end differentiable memory access scheme, which we call Sparse Access Memory (SAM), that retains the representational power of the original approaches whilst training efficiently with very large memories. We show that SAM achieves asymptotic lower bounds in space and time complexity, and find that an implementation runs $1,\!000\times$ faster and with $3,\!000\times$ less physical memory than non-sparse models. SAM learns with comparable data efficiency to existing models on a range of synthetic tasks and one-shot Omniglot character recognition, and can scale to tasks requiring $100,\!000$s of time steps and memories. As well, we show how our approach can be adapted for models that maintain temporal associations between memories, as with the recently introduced Differentiable Neural Computer.