Scaling Memory-Augmented Neural Networks with Sparse Reads and Writes
Paper and Code
Oct 27, 2016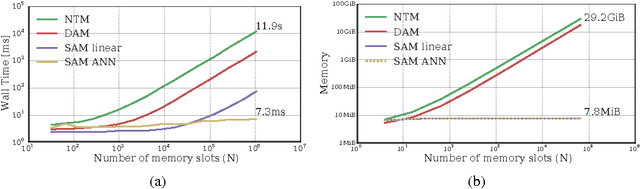
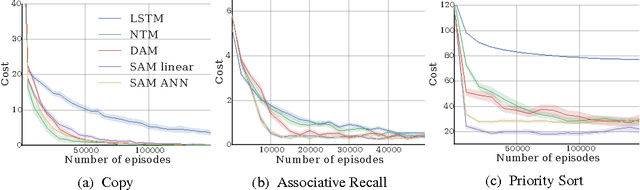
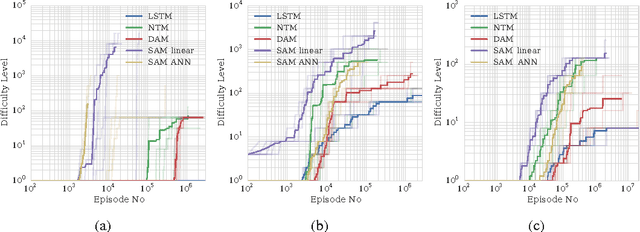
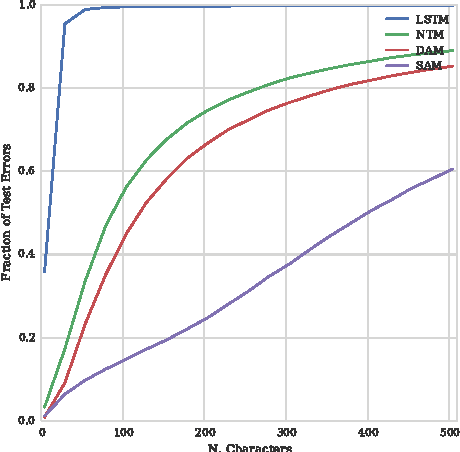
Neural networks augmented with external memory have the ability to learn algorithmic solutions to complex tasks. These models appear promising for applications such as language modeling and machine translation. However, they scale poorly in both space and time as the amount of memory grows --- limiting their applicability to real-world domains. Here, we present an end-to-end differentiable memory access scheme, which we call Sparse Access Memory (SAM), that retains the representational power of the original approaches whilst training efficiently with very large memories. We show that SAM achieves asymptotic lower bounds in space and time complexity, and find that an implementation runs $1,\!000\times$ faster and with $3,\!000\times$ less physical memory than non-sparse models. SAM learns with comparable data efficiency to existing models on a range of synthetic tasks and one-shot Omniglot character recognition, and can scale to tasks requiring $100,\!000$s of time steps and memories. As well, we show how our approach can be adapted for models that maintain temporal associations between memories, as with the recently introduced Differentiable Neural Computer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge