Differentially Private Statistical Inference through $β$-Divergence One Posterior Sampling

Differential privacy guarantees allow the results of a statistical analysis involving sensitive data to be released without compromising the privacy of any individual taking part. Achieving such guarantees generally requires the injection of noise, either directly into parameter estimates or into the estimation process. Instead of artificially introducing perturbations, sampling from Bayesian posterior distributions has been shown to be a special case of the exponential mechanism, producing consistent, and efficient private estimates without altering the data generative process. The application of current approaches has, however, been limited by their strong bounding assumptions which do not hold for basic models, such as simple linear regressors. To ameliorate this, we propose $\beta$D-Bayes, a posterior sampling scheme from a generalised posterior targeting the minimisation of the $\beta$-divergence between the model and the data generating process. This provides private estimation that is generally applicable without requiring changes to the underlying model and consistently learns the data generating parameter. We show that $\beta$D-Bayes produces more precise inference estimation for the same privacy guarantees, and further facilitates differentially private estimation via posterior sampling for complex classifiers and continuous regression models such as neural networks for the first time.

Bias Mitigated Learning from Differentially Private Synthetic Data: A Cautionary Tale

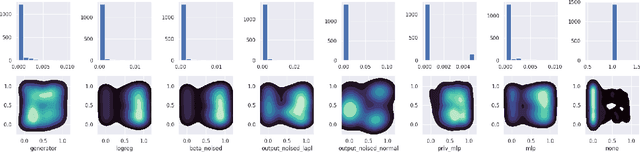
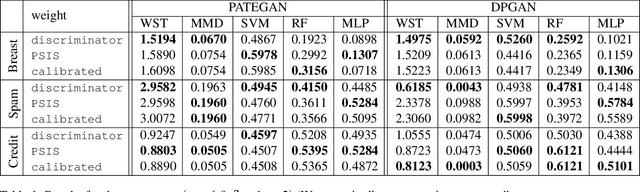
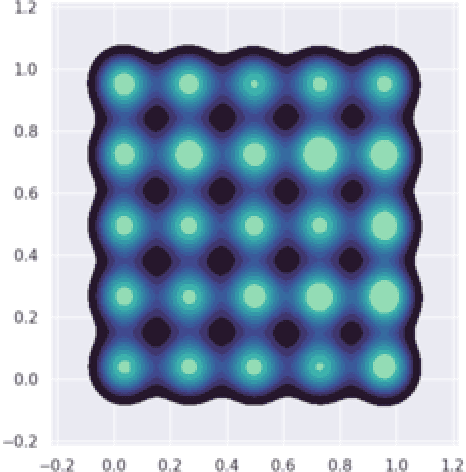
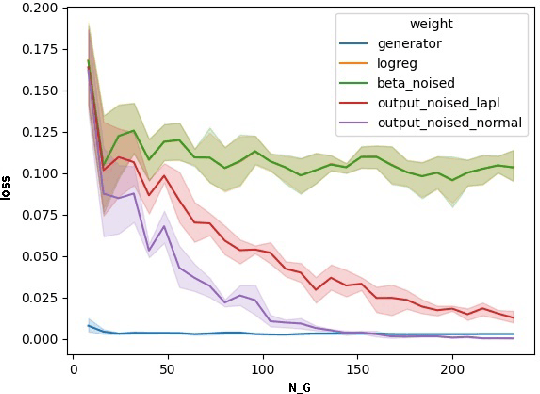
Increasing interest in privacy-preserving machine learning has led to new models for synthetic private data generation from undisclosed real data. However, mechanisms of privacy preservation introduce artifacts in the resulting synthetic data that have a significant impact on downstream tasks such as learning predictive models or inference. In particular, bias can affect all analyses as the synthetic data distribution is an inconsistent estimate of the real-data distribution. We propose several bias mitigation strategies using privatized likelihood ratios that have general applicability to differentially private synthetic data generative models. Through large-scale empirical evaluation, we show that bias mitigation provides simple and effective privacy-compliant augmentation for general applications of synthetic data. However, the work highlights that even after bias correction significant challenges remain on the usefulness of synthetic private data generators for tasks such as prediction and inference.

Foundations of Bayesian Learning from Synthetic Data

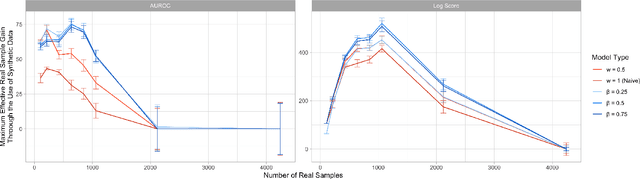
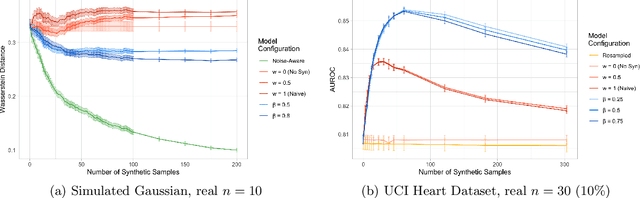
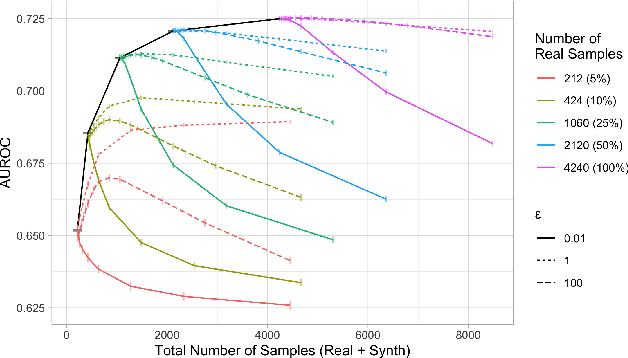
There is significant growth and interest in the use of synthetic data as an enabler for machine learning in environments where the release of real data is restricted due to privacy or availability constraints. Despite a large number of methods for synthetic data generation, there are comparatively few results on the statistical properties of models learnt on synthetic data, and fewer still for situations where a researcher wishes to augment real data with another party's synthesised data. We use a Bayesian paradigm to characterise the updating of model parameters when learning in these settings, demonstrating that caution should be taken when applying conventional learning algorithms without appropriate consideration of the synthetic data generating process and learning task. Recent results from general Bayesian updating support a novel and robust approach to Bayesian synthetic-learning founded on decision theory that outperforms standard approaches across repeated experiments on supervised learning and inference problems.

Generalized Variational Inference

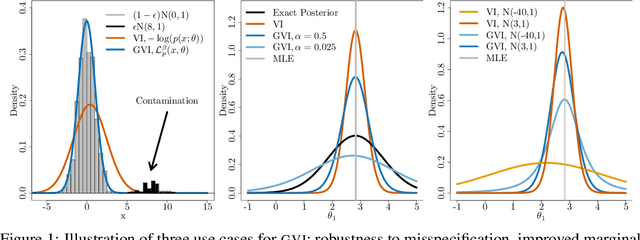
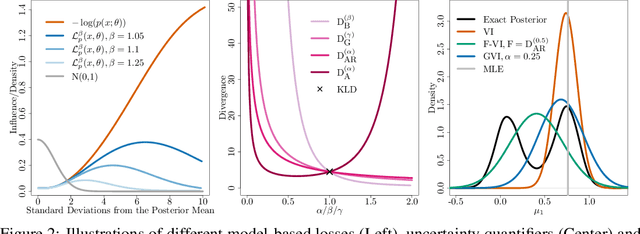
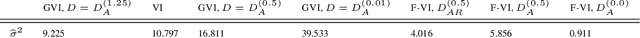
This paper introduces a generalized representation of Bayesian inference. It is derived axiomatically, recovering existing Bayesian methods as special cases. We then use it to prove that variational inference (VI) based on the Kullback-Leibler Divergence with a variational family Q produces the uniquely optimal Q-constrained approximation to the exact Bayesian inference problem. Surprisingly, this implies that standard VI dominates any other Q-constrained approximation to the exact Bayesian inference problem. This means that alternative Q-constrained approximations such as VI minimizing other divergences and Expectation Propagation can produce better posteriors than VI only by implicitly targeting more appropriate Bayesian inference problems. Inspired by this, we introduce Generalized Variational Inference (GVI), a modular approach for instead solving such alternative inference problems explicitly. We explore some applications of GVI, including robustness and better marginals. Lastly, we derive black box GVI and apply it to Bayesian Neural Networks and Deep Gaussian Processes, where GVI can comprehensively outperform competing methods.

Doubly Robust Bayesian Inference for Non-Stationary Streaming Data with $β$-Divergences

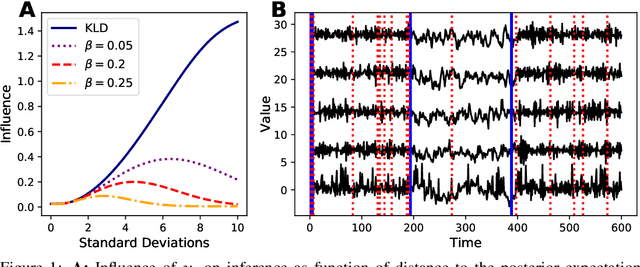
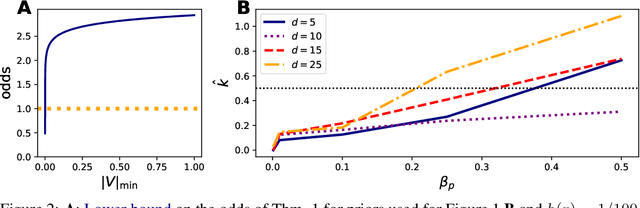
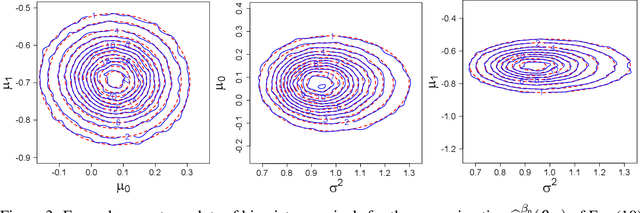
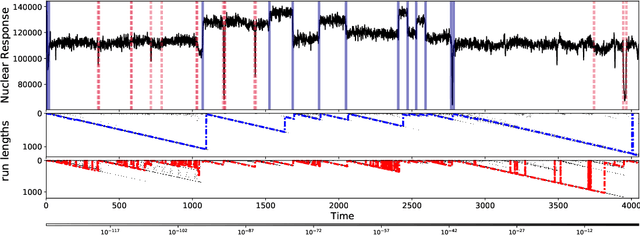
We present the very first robust Bayesian Online Changepoint Detection algorithm through General Bayesian Inference (GBI) with $\beta$-divergences. The resulting inference procedure is doubly robust for both the predictive and the changepoint (CP) posterior, with linear time and constant space complexity. We provide a construction for exponential models and demonstrate it on the Bayesian Linear Regression model. In so doing, we make two additional contributions: Firstly, we make GBI scalable using Structural Variational approximations that are exact as $\beta \to 0$. Secondly, we give a principled way of choosing the divergence parameter $\beta$ by minimizing expected predictive loss on-line. We offer the state of the art and improve the False Discovery Rate of CPs by more than 80% on real world data.