Ivan M. Rosado-Mendez
Constrained and Regularized Quantitative Ultrasound Parameter Estimation using ADMM
Jan 07, 2025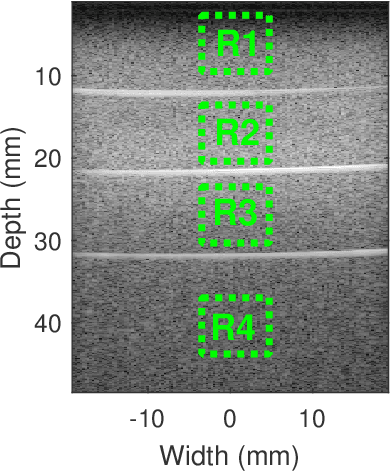


Abstract:Regularized estimation of quantitative ultrasound (QUS) parameters, such as attenuation and backscatter coefficients, has gained research interest. Recently, the alternating direction method of multipliers (ADMM) has been applied successfully to estimate these parameters, by utilizing L2 and L1 norms for attenuation and backscatter coefficient regularization, respectively. While this method improves upon previous approaches, it does not fully leverage the prior knowledge of minimum physically feasible parameter values, sometimes yielding values outside the realistic range. This work addresses this limitation by incorporating minimum QUS parameter values as constraints to enhance ADMM estimation. The proposed method is validated using experimental phantom data.
Uncertainty Decomposition and Error Margin Detection of Homodyned-K Distribution in Quantitative Ultrasound
Sep 17, 2024Abstract:Homodyned K-distribution (HK-distribution) parameter estimation in quantitative ultrasound (QUS) has been recently addressed using Bayesian Neural Networks (BNNs). BNNs have been shown to significantly reduce computational time in speckle statistics-based QUS without compromising accuracy and precision. Additionally, they provide estimates of feature uncertainty, which can guide the clinician's trust in the reported feature value. The total predictive uncertainty in Bayesian modeling can be decomposed into epistemic (uncertainty over the model parameters) and aleatoric (uncertainty inherent in the data) components. By decomposing the predictive uncertainty, we can gain insights into the factors contributing to the total uncertainty. In this study, we propose a method to compute epistemic and aleatoric uncertainties for HK-distribution parameters ($\alpha$ and $k$) estimated by a BNN, in both simulation and experimental data. In addition, we investigate the relationship between the prediction error and both uncertainties, shedding light on the interplay between these uncertainties and HK parameters errors.
Homodyned K-Distribution Parameter Estimation in Quantitative Ultrasound: Autoencoder and Bayesian Neural Network Approaches
Jan 19, 2024



Abstract:Quantitative ultrasound (QUS) analyzes the ultrasound backscattered data to find the properties of scatterers that correlate with the tissue microstructure. Statistics of the envelope of the backscattered radiofrequency (RF) data can be utilized to estimate several QUS parameters. Different distributions have been proposed to model envelope data. The homodyned K-distribution (HK distribution) is one of the most comprehensive distributions that can model ultrasound backscattered envelope data under diverse scattering conditions (varying scatterer number density and coherent scattering). The scatterer clustering parameter (alpha) and the ratio of the coherent to diffuse scattering power (k) are the parameters of this distribution that have been used extensively for tissue characterization in diagnostic ultrasound. The estimation of these two parameters (which we refer to as HK parameters) is done using optimization algorithms in which statistical features such as the envelope point-wise signalto-noise ratio (SNR), skewness, kurtosis, and the log-based moments have been utilized as input to such algorithms. The optimization methods minimize the difference between features and their theoretical value from the HK model. We propose that the true value of these statistical features is a hyperplane that covers a small portion of the feature space. In this paper, we follow two approaches to reduce the effect of sample features' error. We propose a model projection neural network based on denoising autoencoders to project the noisy features into this space based on this assumption. We also investigate if the noise distribution can be learned by the deep estimators. We compare the proposed methods with conventional methods using simulations, an experimental phantom, and data from an in vivo animal model of hepatic steatosis. A demo code are available online at http://code.sonography.ai
A deep learning approach for patchless estimation of ultrasound quantitative parametric image with uncertainty measurement
Feb 24, 2023Abstract:Quantitative ultrasound (QUS) aims to find properties of scatterers which are related to the tissue microstructure. Among different QUS parameters, scatterer number density has been found to be a reliable biomarker for detecting different abnormalities. The homodyned K-distribution (HK-distribution) is a model for the probability density function of the ultrasound echo amplitude that can model different scattering scenarios but requires a large number of samples to be estimated reliably. Parametric images of HK-distribution parameters can be formed by dividing the envelope data into small overlapping patches and estimating parameters within the patches independently. This approach imposes two limiting constraints, the HK-distribution parameters are assumed to be constant within each patch, and each patch requires enough independent samples. In order to mitigate those problems, we employ a deep learning approach to estimate parametric images of scatterer number density (related to HK-distribution shape parameter) without patching. Furthermore, an uncertainty map of the network's prediction is quantified to provide insight about the confidence of the network about the estimated HK parameter values.
Homodyned K-distribution: parameter estimation and uncertainty quantification using Bayesian neural networks
Oct 31, 2022Abstract:Quantitative ultrasound (QUS) allows estimating the intrinsic tissue properties. Speckle statistics are the QUS parameters that describe the first order statistics of ultrasound (US) envelope data. The parameters of Homodyned K-distribution (HK-distribution) are the speckle statistics that can model the envelope data in diverse scattering conditions. However, they require a large amount of data to be estimated reliably. Consequently, finding out the intrinsic uncertainty of the estimated parameters can help us to have a better understanding of the estimated parameters. In this paper, we propose a Bayesian Neural Network (BNN) to estimate the parameters of HK-distribution and quantify the uncertainty of the estimator.
Physics-Inspired Regularized Pulse-Echo Quantitative Ultrasound: Efficient Optimization with ADMM
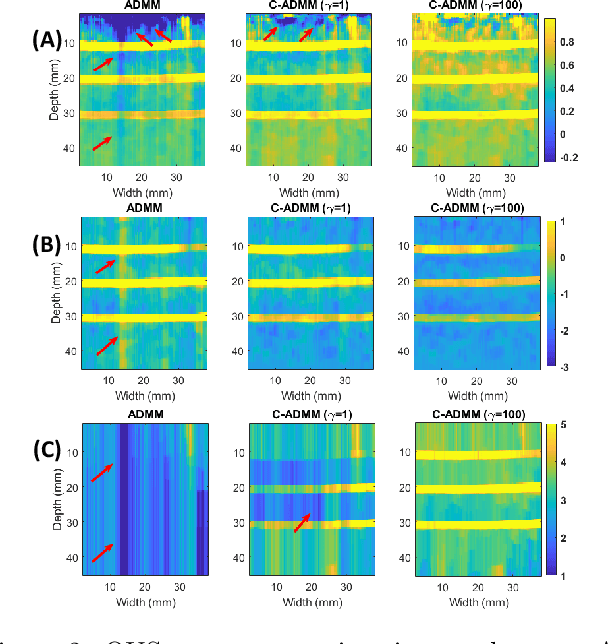
Aug 13, 2022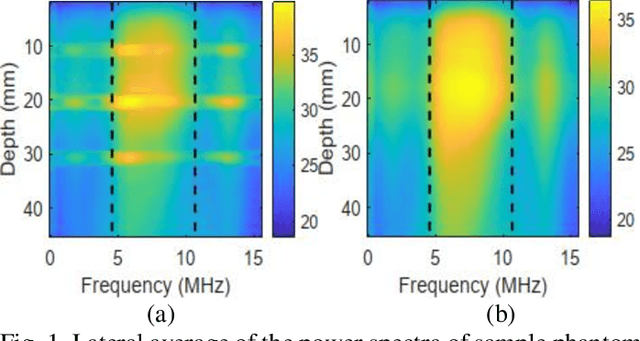
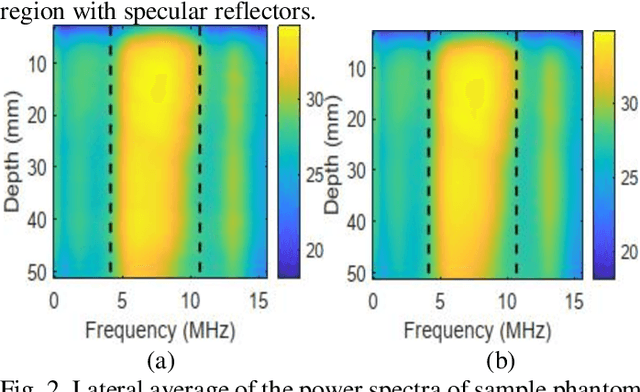
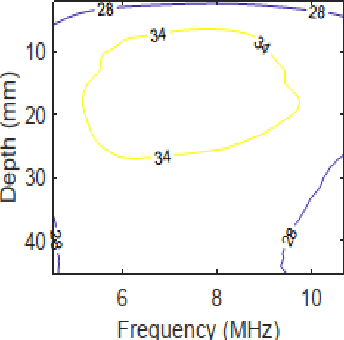
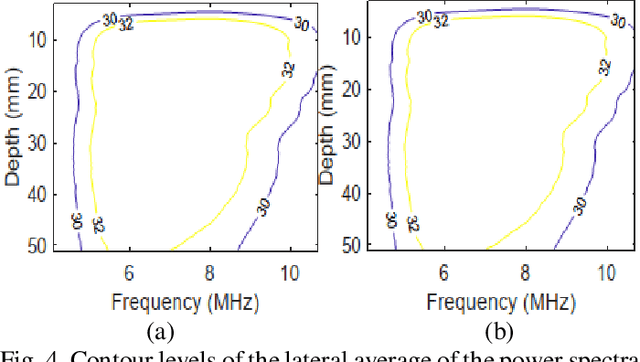
Abstract:Pulse-echo Quantitative ultrasound (PEQUS), which estimates the quantitative properties of tissue microstructure, entails estimating the average attenuation and the backscatter coefficient (BSC). Growing recent research has focused on the regularized estimation of these parameters. Herein, we make two contributions to this field: First, we consider the physics of the average attenuation and backscattering to devise regularization terms accordingly. More specifically, since the average attenuation gradually alters in different parts of the tissue while BSC can vary markedly from tissue to tissue, we apply L2 and L1 norms for the average attenuation and the BSC, respectively. Second, we multiply different frequencies and depths of the power spectra with different weights according to their noise levels. Our rationale is that the high-frequency contents of the power spectra at deep regions have a low signal-to-noise ratio. We exploit the alternating direction method of multipliers (ADMM) for optimizing the cost function. Qualitative and quantitative evaluation of bias and variance exhibit that our proposed algorithm substantially improves the estimations of the average attenuation and the BSC.
Deep Estimation of Speckle Statistics Parametric Images
Jun 08, 2022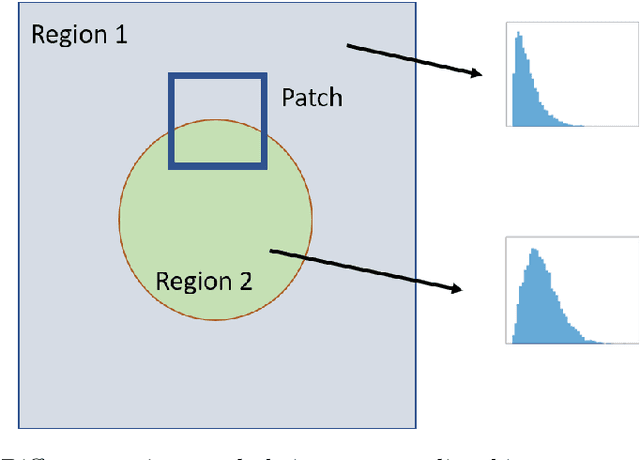

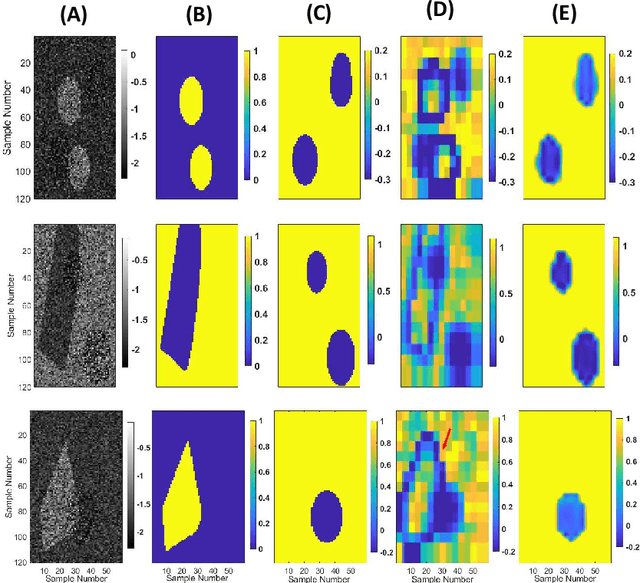

Abstract:Quantitative Ultrasound (QUS) provides important information about the tissue properties. QUS parametric image can be formed by dividing the envelope data into small overlapping patches and computing different speckle statistics such as parameters of the Nakagami and Homodyned K-distributions (HK-distribution). The calculated QUS parametric images can be erroneous since only a few independent samples are available inside the patches. Another challenge is that the envelope samples inside the patch are assumed to come from the same distribution, an assumption that is often violated given that the tissue is usually not homogenous. In this paper, we propose a method based on Convolutional Neural Networks (CNN) to estimate QUS parametric images without patching. We construct a large dataset sampled from the HK-distribution, having regions with random shapes and QUS parameter values. We then use a well-known network to estimate QUS parameters in a multi-task learning fashion. Our results confirm that the proposed method is able to reduce errors and improve border definition in QUS parametric images.
Robust Scatterer Number Density Segmentation of Ultrasound Images
Jan 16, 2022
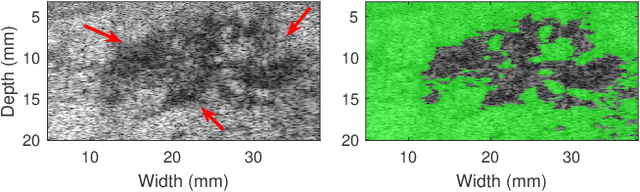
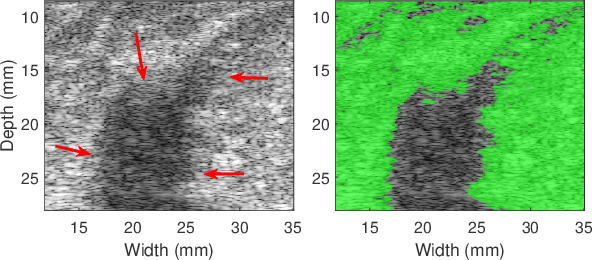
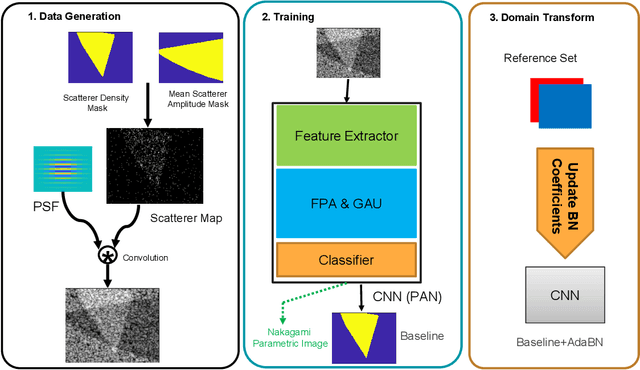
Abstract:Quantitative UltraSound (QUS) aims to reveal information about the tissue microstructure using backscattered echo signals from clinical scanners. Among different QUS parameters, scatterer number density is an important property that can affect estimation of other QUS parameters. Scatterer number density can be classified into high or low scatterer densities. If there are more than 10 scatterers inside the resolution cell, the envelope data is considered as Fully Developed Speckle (FDS) and otherwise, as Under Developed Speckle (UDS). In conventional methods, the envelope data is divided into small overlapping windows (a strategy here we refer to as patching), and statistical parameters such as SNR and skewness are employed to classify each patch of envelope data. However, these parameters are system dependent meaning that their distribution can change by the imaging settings and patch size. Therefore, reference phantoms which have known scatterer number density are imaged with the same imaging settings to mitigate system dependency. In this paper, we aim to segment regions of ultrasound data without any patching. A large dataset is generated which has different shapes of scatterer number density and mean scatterer amplitude using a fast simulation method. We employ a convolutional neural network (CNN) for the segmentation task and investigate the effect of domain shift when the network is tested on different datasets with different imaging settings. Nakagami parametric image is employed for the multi-task learning to improve the performance. Furthermore, inspired by the reference phantom methods in QUS, A domain adaptation stage is proposed which requires only two frames of data from FDS and UDS classes. We evaluate our method for different experimental phantoms and in vivo data.
Estimation of the Scatterer Size Distributions in Quantitative Ultrasound Using Constrained Optimization
Sep 21, 2021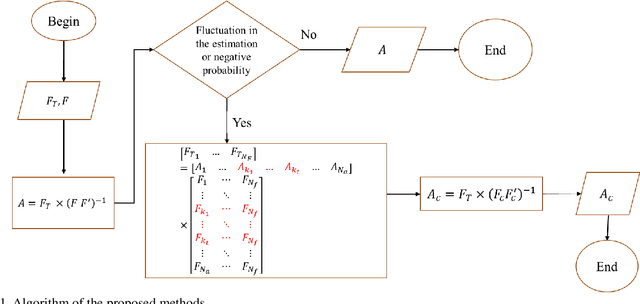
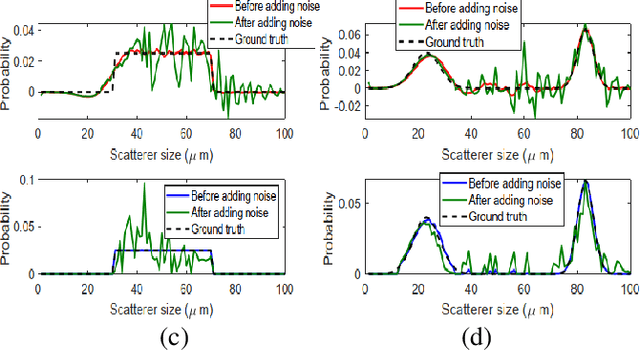
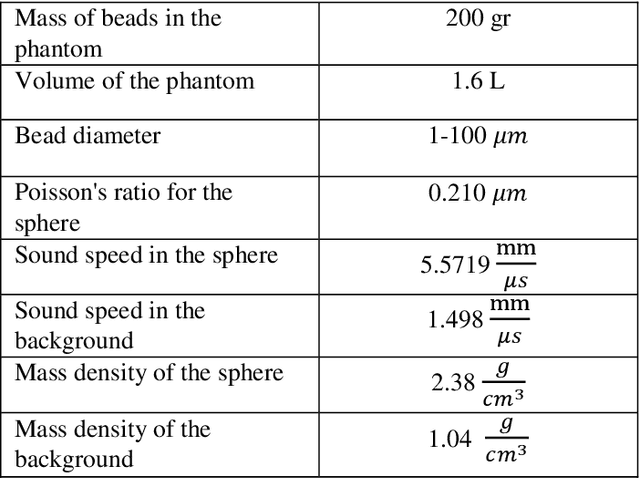
Abstract:Quantitative ultrasound (QUS) parameters such as the effective scatterer diameter (ESD) reveal tissue properties by analyzing ultrasound backscattered echo signal. ESD can be attained through parametrizing backscatter coefficient using form factor models. However, reporting a single scatterer size cannot accurately characterize a tissue, particularly when the media contains scattering sources with a broad range of sizes. Here we estimate the probability of contribution of each scatterer size by modeling the measured form factor as a linear combination of form factors from individual sacatterer sizes. We perform the estimation using two novel techniques. In the first technique, we cast scatterer size distribution as an optimization problem, and efficiently solve it using a linear system of equations. In the second technique, we use the solution of this system of equations to constrain the optimization function, and solve the constrained problem. The methods are evaluated in simulated backscattered coefficients using Faran theory. We evaluate the robustness of the proposed techniques by adding Gaussian noise. The results show that both methods can accurately estimate the scatterer size distribution, and that the second method outperforms the first one.
Ultrasound Scatterer Density Classification Using Convolutional Neural Networks by Exploiting Patch Statistics
Dec 04, 2020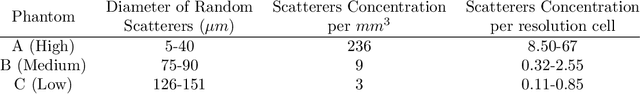
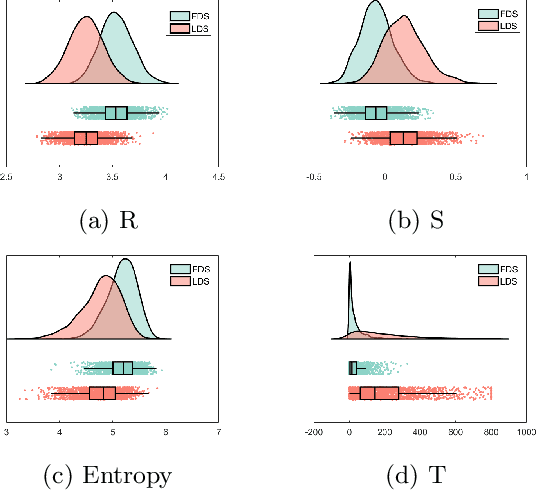
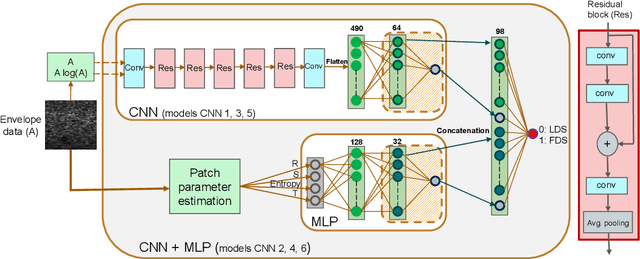
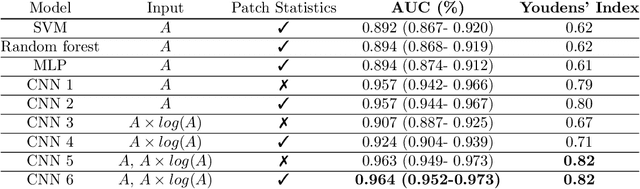
Abstract:Quantitative ultrasound (QUS) can reveal crucial information on tissue properties such as scatterer density. If the scatterer density per resolution cell is above or below 10, the tissue is considered as fully developed speckle (FDS) or low-density scatterers (LDS), respectively. Conventionally, the scatterer density has been classified using estimated statistical parameters of the amplitude of backscattered echoes. However, if the patch size is small, the estimation is not accurate. These parameters are also highly dependent on imaging settings. In this paper, we propose a convolutional neural network (CNN) architecture for QUS, and train it using simulation data. We further improve the network performance by utilizing patch statistics as additional input channels. We evaluate the network using simulation data, experimental phantoms and in vivo data. We also compare our proposed network with different classic and deep learning models, and demonstrate its superior performance in classification of tissues with different scatterer density values. The results also show that the proposed network is able to work with different imaging parameters with no need for a reference phantom. This work demonstrates the potential of CNNs in classifying scatterer density in ultrasound images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge