A deep learning approach for patchless estimation of ultrasound quantitative parametric image with uncertainty measurement

Quantitative ultrasound (QUS) aims to find properties of scatterers which are related to the tissue microstructure. Among different QUS parameters, scatterer number density has been found to be a reliable biomarker for detecting different abnormalities. The homodyned K-distribution (HK-distribution) is a model for the probability density function of the ultrasound echo amplitude that can model different scattering scenarios but requires a large number of samples to be estimated reliably. Parametric images of HK-distribution parameters can be formed by dividing the envelope data into small overlapping patches and estimating parameters within the patches independently. This approach imposes two limiting constraints, the HK-distribution parameters are assumed to be constant within each patch, and each patch requires enough independent samples. In order to mitigate those problems, we employ a deep learning approach to estimate parametric images of scatterer number density (related to HK-distribution shape parameter) without patching. Furthermore, an uncertainty map of the network's prediction is quantified to provide insight about the confidence of the network about the estimated HK parameter values.

Physics-Inspired Regularized Pulse-Echo Quantitative Ultrasound: Efficient Optimization with ADMM

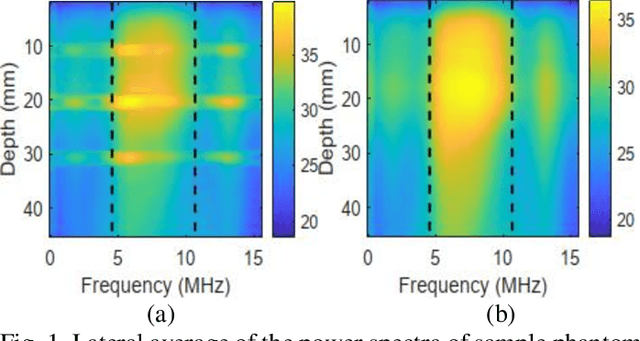
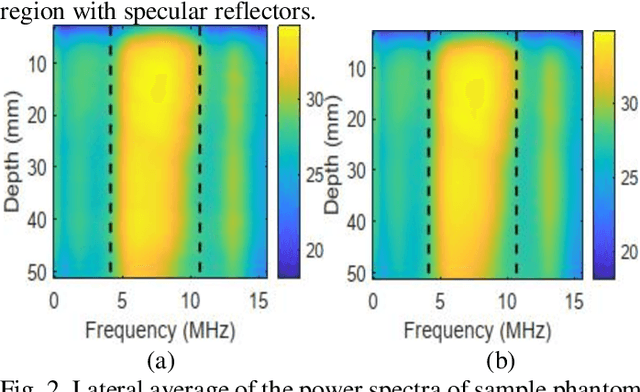
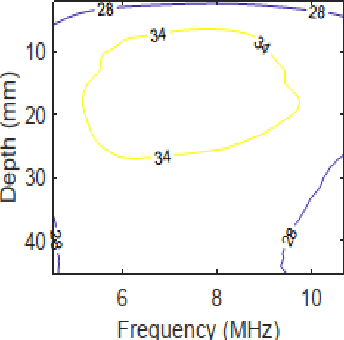
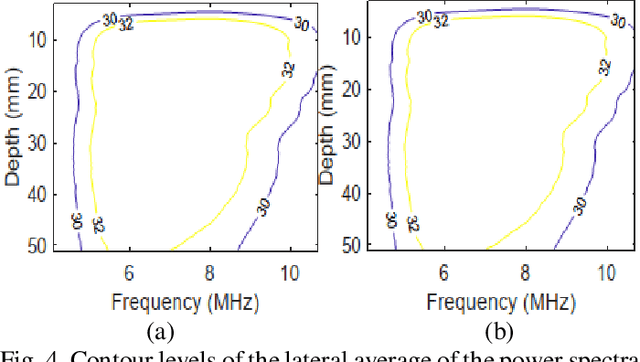
Pulse-echo Quantitative ultrasound (PEQUS), which estimates the quantitative properties of tissue microstructure, entails estimating the average attenuation and the backscatter coefficient (BSC). Growing recent research has focused on the regularized estimation of these parameters. Herein, we make two contributions to this field: First, we consider the physics of the average attenuation and backscattering to devise regularization terms accordingly. More specifically, since the average attenuation gradually alters in different parts of the tissue while BSC can vary markedly from tissue to tissue, we apply L2 and L1 norms for the average attenuation and the BSC, respectively. Second, we multiply different frequencies and depths of the power spectra with different weights according to their noise levels. Our rationale is that the high-frequency contents of the power spectra at deep regions have a low signal-to-noise ratio. We exploit the alternating direction method of multipliers (ADMM) for optimizing the cost function. Qualitative and quantitative evaluation of bias and variance exhibit that our proposed algorithm substantially improves the estimations of the average attenuation and the BSC.