Physics-Inspired Regularized Pulse-Echo Quantitative Ultrasound: Efficient Optimization with ADMM

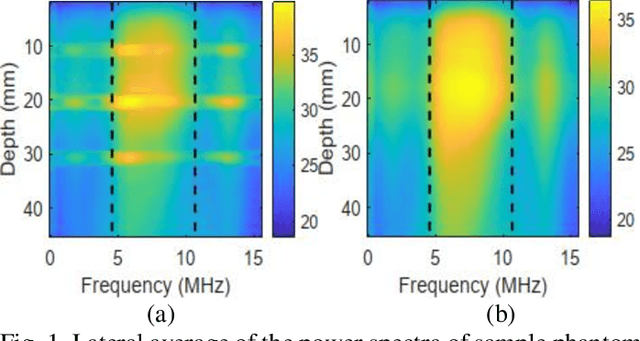
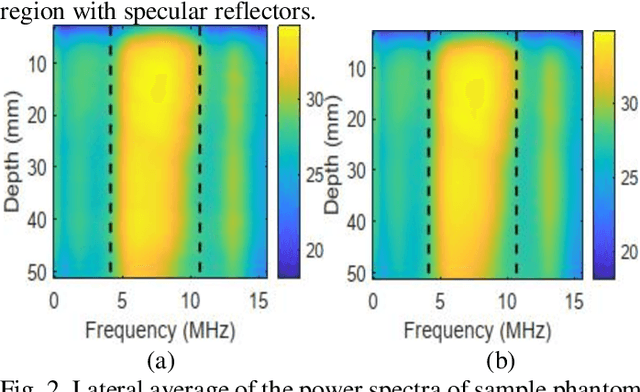
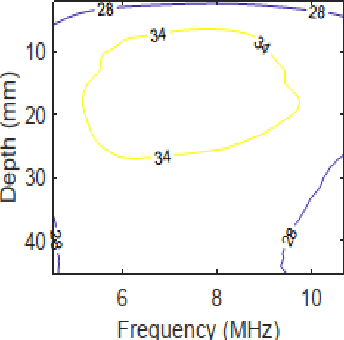
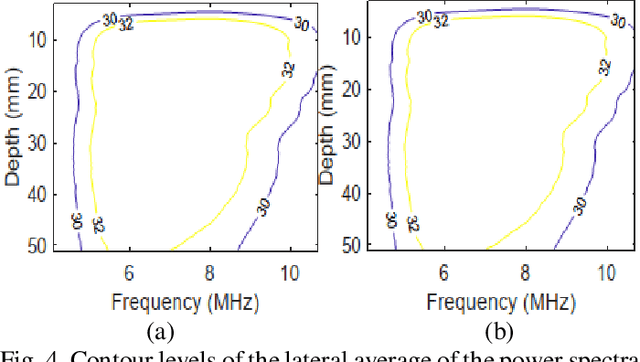
Pulse-echo Quantitative ultrasound (PEQUS), which estimates the quantitative properties of tissue microstructure, entails estimating the average attenuation and the backscatter coefficient (BSC). Growing recent research has focused on the regularized estimation of these parameters. Herein, we make two contributions to this field: First, we consider the physics of the average attenuation and backscattering to devise regularization terms accordingly. More specifically, since the average attenuation gradually alters in different parts of the tissue while BSC can vary markedly from tissue to tissue, we apply L2 and L1 norms for the average attenuation and the BSC, respectively. Second, we multiply different frequencies and depths of the power spectra with different weights according to their noise levels. Our rationale is that the high-frequency contents of the power spectra at deep regions have a low signal-to-noise ratio. We exploit the alternating direction method of multipliers (ADMM) for optimizing the cost function. Qualitative and quantitative evaluation of bias and variance exhibit that our proposed algorithm substantially improves the estimations of the average attenuation and the BSC.

Estimation of the Scatterer Size Distributions in Quantitative Ultrasound Using Constrained Optimization

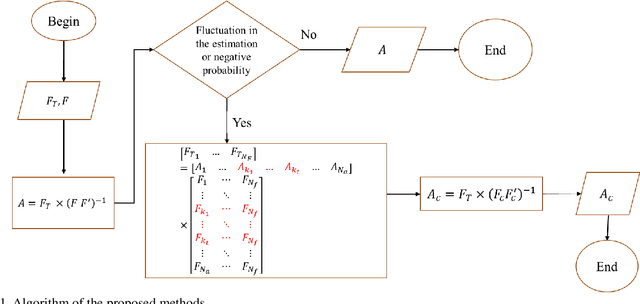
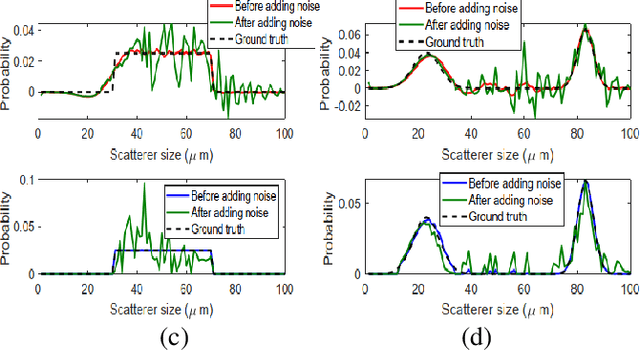
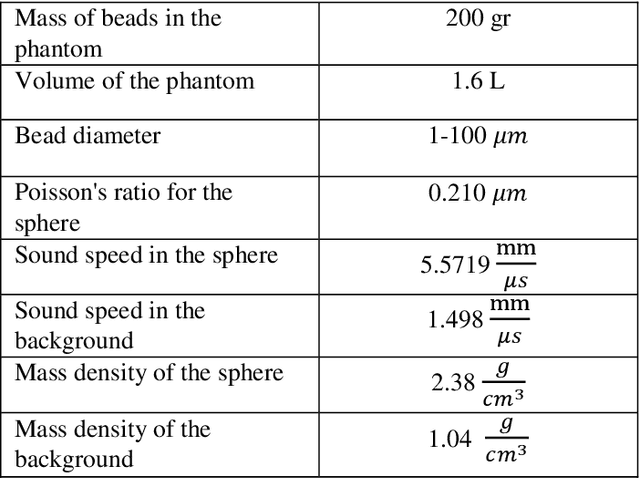
Quantitative ultrasound (QUS) parameters such as the effective scatterer diameter (ESD) reveal tissue properties by analyzing ultrasound backscattered echo signal. ESD can be attained through parametrizing backscatter coefficient using form factor models. However, reporting a single scatterer size cannot accurately characterize a tissue, particularly when the media contains scattering sources with a broad range of sizes. Here we estimate the probability of contribution of each scatterer size by modeling the measured form factor as a linear combination of form factors from individual sacatterer sizes. We perform the estimation using two novel techniques. In the first technique, we cast scatterer size distribution as an optimization problem, and efficiently solve it using a linear system of equations. In the second technique, we use the solution of this system of equations to constrain the optimization function, and solve the constrained problem. The methods are evaluated in simulated backscattered coefficients using Faran theory. We evaluate the robustness of the proposed techniques by adding Gaussian noise. The results show that both methods can accurately estimate the scatterer size distribution, and that the second method outperforms the first one.

Fast and Robust Localization of Surgical Array using Kalman Filter

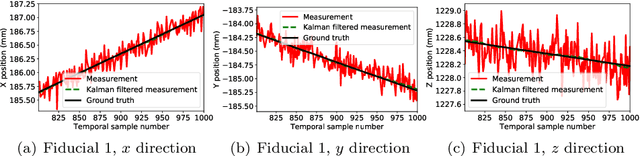
Intraoperative tracking of surgical instruments is an inevitable task of computer-assisted surgery. An optical tracking system often fails to precisely reconstruct the dynamic location and pose of a surgical tool due to the acquisition noise and measurement variance. Embedding a Kalman Filter (KF) or any of its extensions such as extended and unscented Kalman filters with the optical tracker resolves this issue by reducing the estimation variance and regularizing the temporal behavior. However, the current rigid-body KF implementations are computationally burdensome and hence, takes long execution time which hinders real-time surgical tracking. This paper introduces a fast and computationally efficient implementation of linear KF to improve the measurement accuracy of an optical tracking system with high temporal resolution. Instead of the surgical tool as a whole, our KF framework tracks each individual fiducial mounted on it using a Newtonian model. In addition to simulated dataset, we validate our technique against real data obtained from a high frame-rate commercial optical tracking system. The proposed KF framework substantially stabilizes the tracking behavior in all of our experiments and reduces the mean-squared error (MSE) from the order of $10^{-2}$ $mm^{2}$ to $10^{-4}$ $mm^{2}$.