Enhancing Convolutional Neural Networks with Higher-Order Numerical Difference Methods

With the rise of deep learning technology in practical applications, Convolutional Neural Networks (CNNs) have been able to assist humans in solving many real-world problems. To enhance the performance of CNNs, numerous network architectures have been explored. Some of these architectures are designed based on the accumulated experience of researchers over time, while others are designed through neural architecture search methods. The improvements made to CNNs by the aforementioned methods are quite significant, but most of the improvement methods are limited in reality by model size and environmental constraints, making it difficult to fully realize the improved performance. In recent years, research has found that many CNN structures can be explained by the discretization of ordinary differential equations. This implies that we can design theoretically supported deep network structures using higher-order numerical difference methods. It should be noted that most of the previous CNN model structures are based on low-order numerical methods. Therefore, considering that the accuracy of linear multi-step numerical difference methods is higher than that of the forward Euler method, this paper proposes a stacking scheme based on the linear multi-step method. This scheme enhances the performance of ResNet without increasing the model size and compares it with the Runge-Kutta scheme. The experimental results show that the performance of the stacking scheme proposed in this paper is superior to existing stacking schemes (ResNet and HO-ResNet), and it has the capability to be extended to other types of neural networks.

Enhancing Deep Learning with Optimized Gradient Descent: Bridging Numerical Methods and Neural Network Training

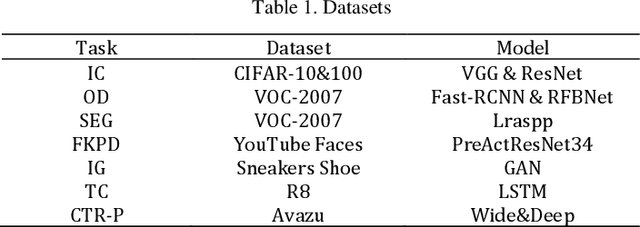
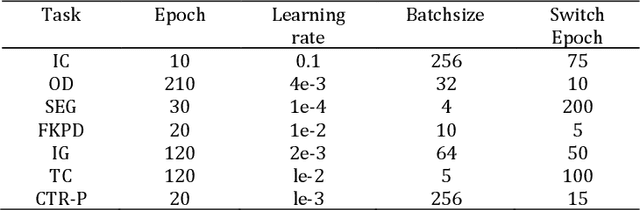
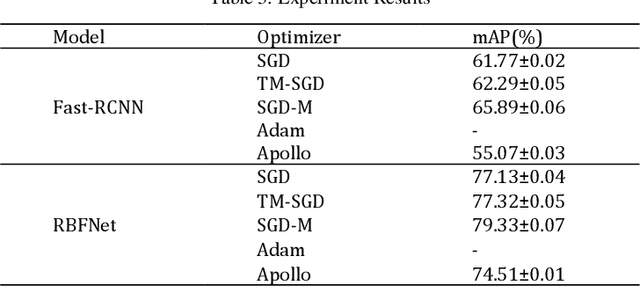
Optimization theory serves as a pivotal scientific instrument for achieving optimal system performance, with its origins in economic applications to identify the best investment strategies for maximizing benefits. Over the centuries, from the geometric inquiries of ancient Greece to the calculus contributions by Newton and Leibniz, optimization theory has significantly advanced. The persistent work of scientists like Lagrange, Cauchy, and von Neumann has fortified its progress. The modern era has seen an unprecedented expansion of optimization theory applications, particularly with the growth of computer science, enabling more sophisticated computational practices and widespread utilization across engineering, decision analysis, and operations research. This paper delves into the profound relationship between optimization theory and deep learning, highlighting the omnipresence of optimization problems in the latter. We explore the gradient descent algorithm and its variants, which are the cornerstone of optimizing neural networks. The chapter introduces an enhancement to the SGD optimizer, drawing inspiration from numerical optimization methods, aiming to enhance interpretability and accuracy. Our experiments on diverse deep learning tasks substantiate the improved algorithm's efficacy. The paper concludes by emphasizing the continuous development of optimization theory and its expanding role in solving intricate problems, enhancing computational capabilities, and informing better policy decisions.

Research on Deep Learning Model of Feature Extraction Based on Convolutional Neural Network

Neural networks with relatively shallow layers and simple structures may have limited ability in accurately identifying pneumonia. In addition, deep neural networks also have a large demand for computing resources, which may cause convolutional neural networks to be unable to be implemented on terminals. Therefore, this paper will carry out the optimal classification of convolutional neural networks. Firstly, according to the characteristics of pneumonia images, AlexNet and InceptionV3 were selected to obtain better image recognition results. Combining the features of medical images, the forward neural network with deeper and more complex structure is learned. Finally, knowledge extraction technology is used to extract the obtained data into the AlexNet model to achieve the purpose of improving computing efficiency and reducing computing costs. The results showed that the prediction accuracy, specificity, and sensitivity of the trained AlexNet model increased by 4.25 percentage points, 7.85 percentage points, and 2.32 percentage points, respectively. The graphics processing usage has decreased by 51% compared to the InceptionV3 mode.