Optimizing YOLOv5s Object Detection through Knowledge Distillation algorithm

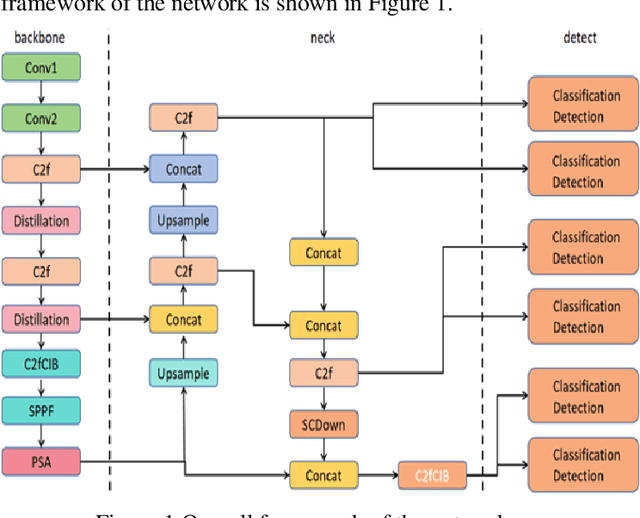
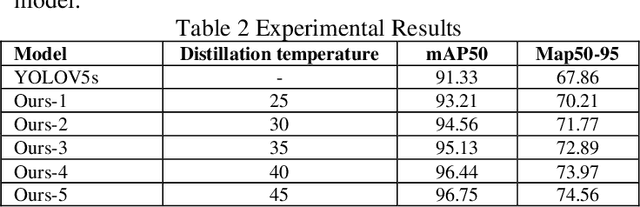
This paper explores the application of knowledge distillation technology in target detection tasks, especially the impact of different distillation temperatures on the performance of student models. By using YOLOv5l as the teacher network and a smaller YOLOv5s as the student network, we found that with the increase of distillation temperature, the student's detection accuracy gradually improved, and finally achieved mAP50 and mAP50-95 indicators that were better than the original YOLOv5s model at a specific temperature. Experimental results show that appropriate knowledge distillation strategies can not only improve the accuracy of the model but also help improve the reliability and stability of the model in practical applications. This paper also records in detail the accuracy curve and loss function descent curve during the model training process and shows that the model converges to a stable state after 150 training cycles. These findings provide a theoretical basis and technical reference for further optimizing target detection algorithms.

Enhancing Deep Learning with Optimized Gradient Descent: Bridging Numerical Methods and Neural Network Training

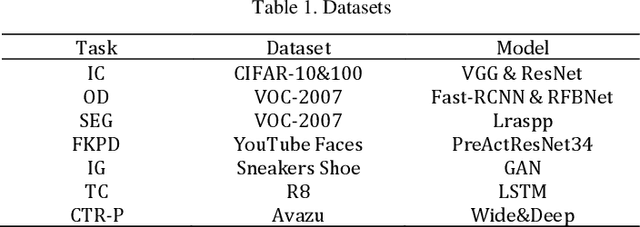
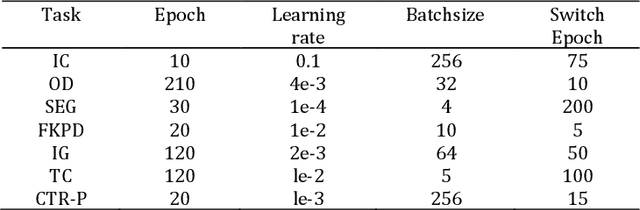
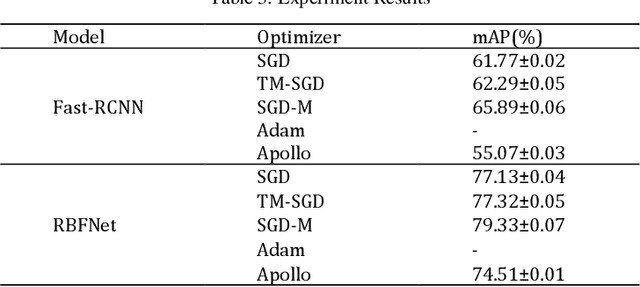
Optimization theory serves as a pivotal scientific instrument for achieving optimal system performance, with its origins in economic applications to identify the best investment strategies for maximizing benefits. Over the centuries, from the geometric inquiries of ancient Greece to the calculus contributions by Newton and Leibniz, optimization theory has significantly advanced. The persistent work of scientists like Lagrange, Cauchy, and von Neumann has fortified its progress. The modern era has seen an unprecedented expansion of optimization theory applications, particularly with the growth of computer science, enabling more sophisticated computational practices and widespread utilization across engineering, decision analysis, and operations research. This paper delves into the profound relationship between optimization theory and deep learning, highlighting the omnipresence of optimization problems in the latter. We explore the gradient descent algorithm and its variants, which are the cornerstone of optimizing neural networks. The chapter introduces an enhancement to the SGD optimizer, drawing inspiration from numerical optimization methods, aiming to enhance interpretability and accuracy. Our experiments on diverse deep learning tasks substantiate the improved algorithm's efficacy. The paper concludes by emphasizing the continuous development of optimization theory and its expanding role in solving intricate problems, enhancing computational capabilities, and informing better policy decisions.