LLM Inference Acceleration via Efficient Operation Fusion

The rapid development of the Transformer-based Large Language Models (LLMs) in recent years has been closely linked to their ever-growing and already enormous sizes. Many LLMs contain hundreds of billions of parameters and require dedicated hardware resources for training and inference. One of the key challenges inherent to the Transformer architecture is the requirement to support numerous non-linear transformations that involves normalization. For instance, each decoder block typically contains at least one Softmax operation and two Layernorms. The computation of the corresponding normalization scaling factors becomes a major bottleneck as it requires spatial collective operations. In other words, when it comes to the computation of denominators for Softmax and Layernorm, all vector elements must be aggregated into a single location, requiring significant communication. These collective operations slow down inference on Transformers by approximately 20%, defeating the whole purpose of distributed in-memory compute. In this work, we propose an extremely efficient technique that can completely hide the overhead caused by such collective operations. Note that each Softmax and Layernorm operation is typically followed by a linear layer. Since non-linear and linear operations are performed on different hardware engines, they can be easily parallelized once the algebra allows such commutation. By leveraging the inherent properties of linear operations, we can defer the normalization of the preceding Softmax and Layernorm until after the linear layer is computed. Now we can compute the collective scaling factors concurrently with the matrix multiplication and completely hide the latency of the former behind the latter. Such parallelization preserves the numerical accuracy while significantly improving the hardware utilization and reducing the overall latency.

SLaNC: Static LayerNorm Calibration

The ever increasing sizes of Large Language Models (LLMs) beyond hundreds of billions of parameters have generated enormous pressure on the manufacturers of dedicated hardware accelerators and made the innovative design of the latter one of the most rapidly expanding fields of the AI industry. Various approaches have been explored to enable efficient and accurate processing of LLMs on the available accelerators given their computational and storage limitations. Among these, various quantization techniques have become the main focus of the community as a means of reducing the compute, communication and storage requirements. Quantization to lower precision formats naturally poses a number of challenges caused by the limited range of the available value representations. When it comes to processing the popular Transformer models on hardware, one of the main issues becomes calculation of the LayerNorm simply because accumulation of the variance requires a much wider dynamic range than the hardware enables. In this article, we address this matter and propose a computationally-efficient scaling technique that can be easily applied to Transformer models during inference. Our method suggests a straightforward way of scaling the LayerNorm inputs based on the static weights of the immediately preceding linear layers. The scaling factors are computed offline, based solely on the linear layer weights, hence no latency or computational overhead is added during inference. Most importantly, our technique ensures that no numerical issues such as overflow or underflow could happen during the compute. This approach offers smooth, accurate and resource-effective inference across a wide range of hardware architectures. The article provides theoretical justification as well as supporting numerical simulations.

Accurate Block Quantization in LLMs with Outliers

The demand for inference on extremely large scale LLMs has seen enormous growth in the recent months. It made evident the colossal shortage of dedicated hardware capable of efficient and fast processing of the involved compute and memory movement. The problem is aggravated by the exploding raise in the lengths of the sequences being processed, since those require efficient on-chip storage of the KV-cache of size proportional to the sequence length. To make the required compute feasible and fit the involved data into available memory, numerous quantization techniques have been proposed that allow accurate quantization for both weights and activations. One of the main recent breakthroughs in this direction was introduction of the family of Block Floating Point (BFP) formats characterized by a block of mantissas with a shared scale factor. These enable memory- power-, and compute- efficient hardware support of the tensor operations and provide extremely good quantization accuracy. The main issues preventing widespread application of block formats is caused by the presence of outliers in weights and activations since those affect the accuracy of the other values in the same block. In this paper, we focus on the most critical problem of limited KV-cache storage. We propose a novel approach enabling usage of low precision BFP formats without compromising the resulting model accuracy. We exploit the common channel-wise patterns exhibited by the outliers to rearrange them in such a way, that their quantization quality is significantly improved. The methodology yields 2x savings in the memory footprint without significant degradation of the model's accuracy. Importantly, the rearrangement of channels happens at the compile time and thus has no impact on the inference latency.

Keyformer: KV Cache Reduction through Key Tokens Selection for Efficient Generative Inference

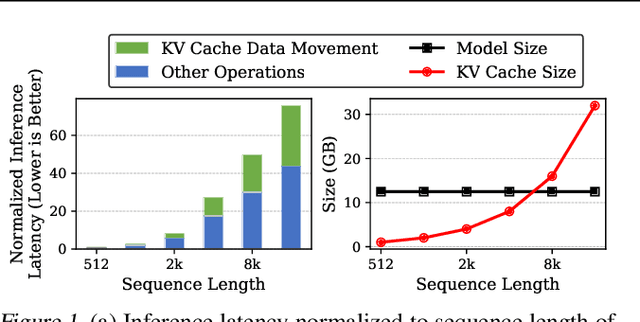
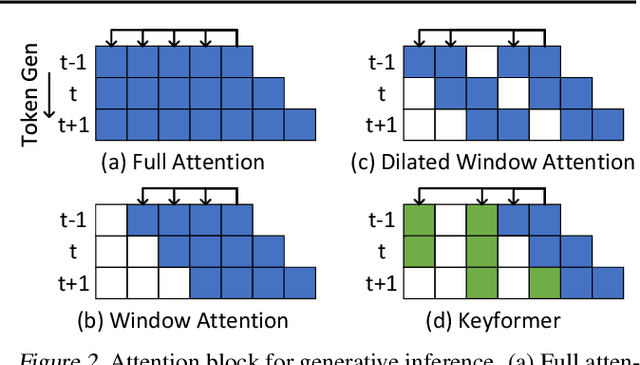
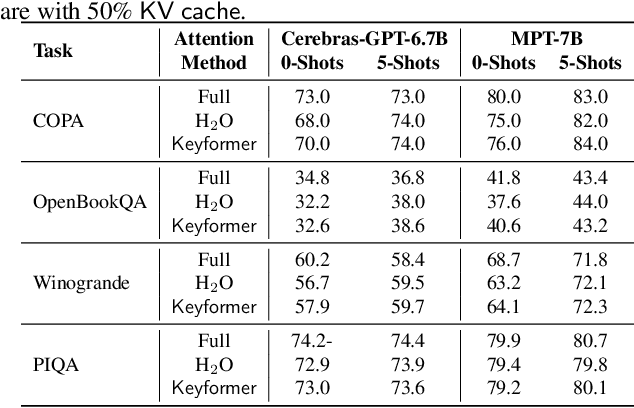
Transformers have emerged as the underpinning architecture for Large Language Models (LLMs). In generative language models, the inference process involves two primary phases: prompt processing and token generation. Token generation, which constitutes the majority of the computational workload, primarily entails vector-matrix multiplications and interactions with the Key-Value (KV) Cache. This phase is constrained by memory bandwidth due to the overhead of transferring weights and KV cache values from the memory system to the computing units. This memory bottleneck becomes particularly pronounced in applications that require long-context and extensive text generation, both of which are increasingly crucial for LLMs. This paper introduces "Keyformer", an innovative inference-time approach, to mitigate the challenges associated with KV cache size and memory bandwidth utilization. Keyformer leverages the observation that approximately 90% of the attention weight in generative inference focuses on a specific subset of tokens, referred to as "key" tokens. Keyformer retains only the key tokens in the KV cache by identifying these crucial tokens using a novel score function. This approach effectively reduces both the KV cache size and memory bandwidth usage without compromising model accuracy. We evaluate Keyformer's performance across three foundational models: GPT-J, Cerebras-GPT, and MPT, which employ various positional embedding algorithms. Our assessment encompasses a variety of tasks, with a particular emphasis on summarization and conversation tasks involving extended contexts. Keyformer's reduction of KV cache reduces inference latency by 2.1x and improves token generation throughput by 2.4x, while preserving the model's accuracy.

Error Probability Bounds for Invariant Causal Prediction via Multiple Access Channels

We consider the problem of lower bounding the error probability under the invariant causal prediction (ICP) framework. To this end, we examine and draw connections between ICP and the zero-rate Gaussian multiple access channel by first proposing a variant of the original invariant prediction assumption, and then considering a special case of the Gaussian multiple access channel where a codebook is shared between an unknown number of senders. This connection allows us to develop three types of lower bounds on the error probability, each with different assumptions and constraints, leveraging techniques for multiple access channels. The proposed bounds are evaluated with respect to existing causal discovery methods as well as a proposed heuristic method based on minimum distance decoding.

Block Format Error Bounds and Optimal Block Size Selection

The amounts of data that need to be transmitted, processed, and stored by the modern deep neural networks have reached truly enormous volumes in the last few years calling for the invention of new paradigms both in hardware and software development. One of the most promising and rapidly advancing frontiers here is the creation of new data formats. In this work we focus on the family of block floating point numerical formats due to their combination of wide dynamic range, numerical accuracy, and efficient hardware implementation of inner products using simple integer arithmetic. These formats are characterized by a block of mantissas with a shared scale factor. The basic Block Floating Point (BFP) format quantizes the block scales into the nearest powers of two on the right. Its simple modification - Scaled BFP (SBFP) - stores the same scales in full precision and thus allows higher accuracy. In this paper, we study the statistical behavior of both these formats rigorously. We develop asymptotic bounds on the inner product error in SBFP- and BFP-quantized normally distributed vectors. Next, we refine those asymptotic results to finite dimensional settings and derive high-dimensional tight bounds for the same errors. Based on the obtained results we introduce a performance metric assessing accuracy of any block format. This metric allows us to determine the optimal parameters, such as the block size, yielding highest accuracy. In particular, we show that if the precision of the BFP format is fixed at 4 bits, the optimal block size becomes 64. All theoretical derivations are supported by numerical experiments and studies on the weights of publicly available pretrained neural networks.

Lower Bounds on the Error Probability for Invariant Causal Prediction

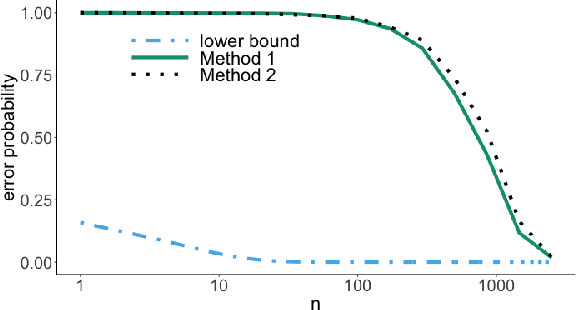
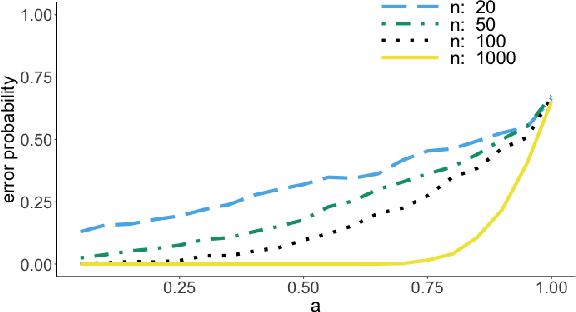
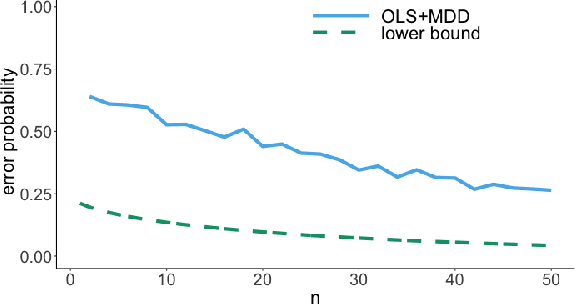
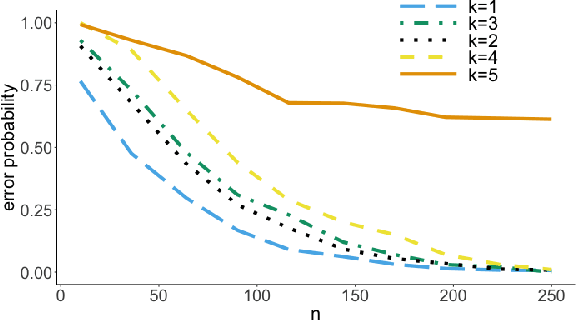
It is common practice to collect observations of feature and response pairs from different environments. A natural question is how to identify features that have consistent prediction power across environments. The invariant causal prediction framework proposes to approach this problem through invariance, assuming a linear model that is invariant under different environments. In this work, we make an attempt to shed light on this framework by connecting it to the Gaussian multiple access channel problem. Specifically, we incorporate optimal code constructions and decoding methods to provide lower bounds on the error probability. We illustrate our findings by various simulation settings.

Reliable Covariance Estimation

Covariance or scatter matrix estimation is ubiquitous in most modern statistical and machine learning applications. The task becomes especially challenging since most real-world datasets are essentially non-Gaussian. The data is often contaminated by outliers and/or has heavy-tailed distribution causing the sample covariance to behave very poorly and calling for robust estimation methodology. The natural framework for the robust scatter matrix estimation is based on elliptical populations. Here, Tyler's estimator stands out by being distribution-free within the elliptical family and easy to compute. The existing works thoroughly study the performance of Tyler's estimator assuming ellipticity but without providing any tools to verify this assumption when the covariance is unknown in advance. We address the following open question: Given the sampled data and having no prior on the data generating process, how to assess the quality of the scatter matrix estimator? In this work we show that this question can be reformulated as an asymptotic uniformity test for certain sequences of exchangeable vectors on the unit sphere. We develop a consistent and easily applicable goodness-of-fit test against all alternatives to ellipticity when the scatter matrix is unknown. The findings are supported by numerical simulations demonstrating the power of the suggest technique.

Stationary Geometric Graphical Model Selection

We consider the problem of model selection in Gaussian Markov fields in the sample deficient scenario. In many practically important cases, the underlying networks are embedded into Euclidean spaces. Using the natural geometric structure, we introduce the notion of spatially stationary distributions over geometric graphs. This directly generalizes the notion of stationary time series to the multidimensional setting lacking time axis. We show that the idea of spatial stationarity leads to a dramatic decrease in the sample complexity of the model selection compared to abstract graphs with the same level of sparsity. For geometric graphs on randomly spread vertices and edges of bounded length, we develop tight information-theoretic bounds on sample complexity and show that a finite number of independent samples is sufficient for a consistent recovery. Finally, we develop an efficient technique capable of reliably and consistently reconstructing graphs with a bounded number of measurements.

Region Detection in Markov Random Fields: Gaussian Case

We consider the problem of model selection in Gaussian Markov fields in the sample deficient scenario. The benchmark information-theoretic results in the case of d-regular graphs require the number of samples to be at least proportional to the logarithm of the number of vertices to allow consistent graph recovery. When the number of samples is less than this amount, reliable detection of all edges is impossible. In many applications, it is more important to learn the distribution of the edge (coupling) parameters over the network than the specific locations of the edges. Assuming that the entire graph can be partitioned into a number of spatial regions with similar edge parameters and reasonably regular boundaries, we develop new information-theoretic sample complexity bounds and show that a bounded number of samples can be sufficient to consistently recover these regions. Finally, we introduce and analyze an efficient region growing algorithm capable of recovering the regions with high accuracy. We show that it is consistent and demonstrate its performance benefits in synthetic simulations.