Mining Invariance from Nonlinear Multi-Environment Data: Binary Classification

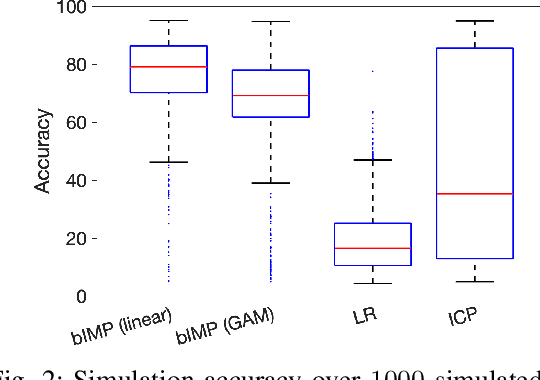
Making predictions in an unseen environment given data from multiple training environments is a challenging task. We approach this problem from an invariance perspective, focusing on binary classification to shed light on general nonlinear data generation mechanisms. We identify a unique form of invariance that exists solely in a binary setting that allows us to train models invariant over environments. We provide sufficient conditions for such invariance and show it is robust even when environmental conditions vary greatly. Our formulation admits a causal interpretation, allowing us to compare it with various frameworks. Finally, we propose a heuristic prediction method and conduct experiments using real and synthetic datasets.

Error Probability Bounds for Invariant Causal Prediction via Multiple Access Channels

We consider the problem of lower bounding the error probability under the invariant causal prediction (ICP) framework. To this end, we examine and draw connections between ICP and the zero-rate Gaussian multiple access channel by first proposing a variant of the original invariant prediction assumption, and then considering a special case of the Gaussian multiple access channel where a codebook is shared between an unknown number of senders. This connection allows us to develop three types of lower bounds on the error probability, each with different assumptions and constraints, leveraging techniques for multiple access channels. The proposed bounds are evaluated with respect to existing causal discovery methods as well as a proposed heuristic method based on minimum distance decoding.

Lower Bounds on the Error Probability for Invariant Causal Prediction

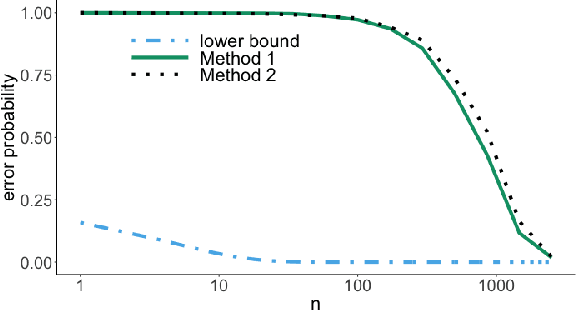
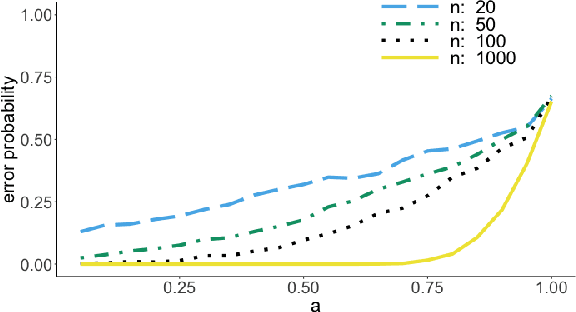
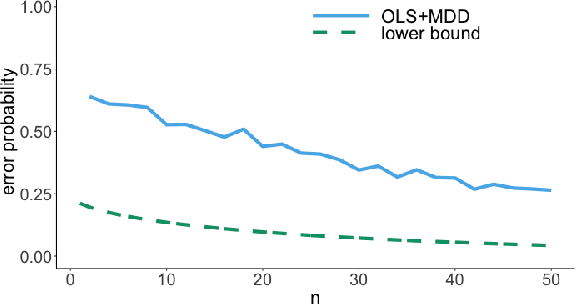
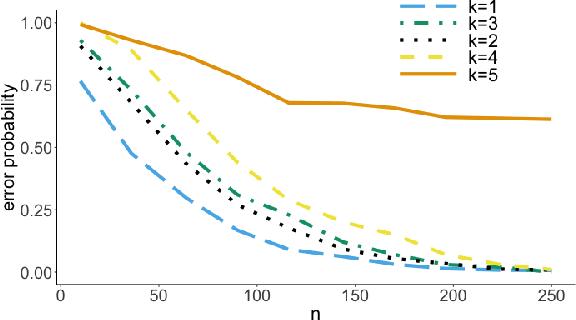
It is common practice to collect observations of feature and response pairs from different environments. A natural question is how to identify features that have consistent prediction power across environments. The invariant causal prediction framework proposes to approach this problem through invariance, assuming a linear model that is invariant under different environments. In this work, we make an attempt to shed light on this framework by connecting it to the Gaussian multiple access channel problem. Specifically, we incorporate optimal code constructions and decoding methods to provide lower bounds on the error probability. We illustrate our findings by various simulation settings.

A Subsampling-Based Method for Causal Discovery on Discrete Data

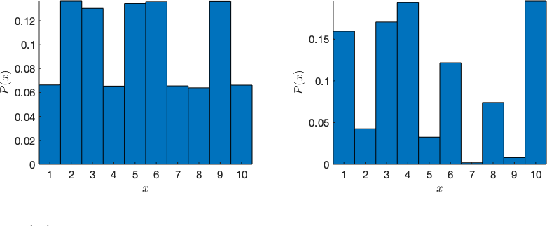
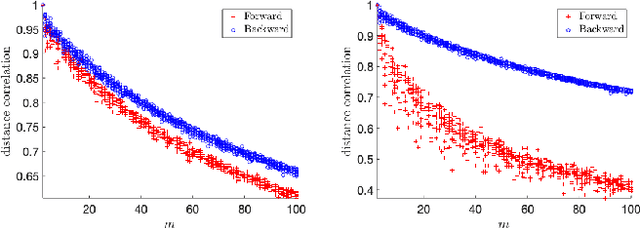
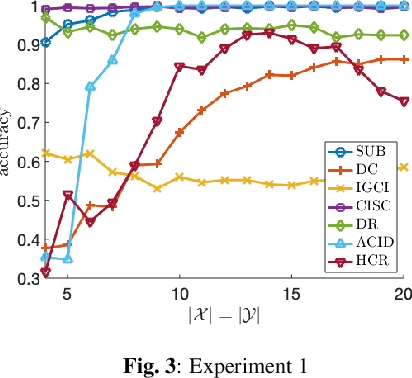
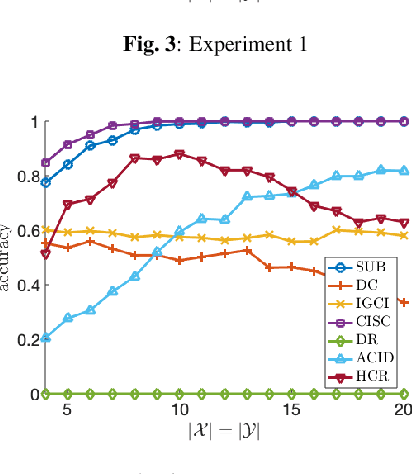
Inferring causal directions on discrete and categorical data is an important yet challenging problem. Even though the additive noise models (ANMs) approach can be adapted to the discrete data, the functional structure assumptions make it not applicable on categorical data. Inspired by the principle that the cause and mechanism are independent, various methods have been developed, leveraging independence tests such as the distance correlation measure. In this work, we take an alternative perspective and propose a subsampling-based method to test the independence between the generating schemes of the cause and that of the mechanism. Our methodology works for both discrete and categorical data and does not imply any functional model on the data, making it a more flexible approach. To demonstrate the efficacy of our methodology, we compare it with existing baselines over various synthetic data and real data experiments.