Neural-BO: A Black-box Optimization Algorithm using Deep Neural Networks

Bayesian Optimization (BO) is an effective approach for global optimization of black-box functions when function evaluations are expensive. Most prior works use Gaussian processes to model the black-box function, however, the use of kernels in Gaussian processes leads to two problems: first, the kernel-based methods scale poorly with the number of data points and second, kernel methods are usually not effective on complex structured high dimensional data due to curse of dimensionality. Therefore, we propose a novel black-box optimization algorithm where the black-box function is modeled using a neural network. Our algorithm does not need a Bayesian neural network to estimate predictive uncertainty and is therefore computationally favorable. We analyze the theoretical behavior of our algorithm in terms of regret bound using advances in NTK theory showing its efficient convergence. We perform experiments with both synthetic and real-world optimization tasks and show that our algorithm is more sample efficient compared to existing methods.

Regret Bounds for Expected Improvement Algorithms in Gaussian Process Bandit Optimization

The expected improvement (EI) algorithm is one of the most popular strategies for optimization under uncertainty due to its simplicity and efficiency. Despite its popularity, the theoretical aspects of this algorithm have not been properly analyzed. In particular, whether in the noisy setting, the EI strategy with a standard incumbent converges is still an open question of the Gaussian process bandit optimization problem. We aim to answer this question by proposing a variant of EI with a standard incumbent defined via the GP predictive mean. We prove that our algorithm converges, and achieves a cumulative regret bound of $\mathcal O(\gamma_T\sqrt{T})$, where $\gamma_T$ is the maximum information gain between $T$ observations and the Gaussian process model. Based on this variant of EI, we further propose an algorithm called Improved GP-EI that converges faster than previous counterparts. In particular, our proposed variants of EI do not require the knowledge of the RKHS norm and the noise's sub-Gaussianity parameter as in previous works. Empirical validation in our paper demonstrates the effectiveness of our algorithms compared to several baselines.

Combining Online Learning and Offline Learning for Contextual Bandits with Deficient Support

We address policy learning with logged data in contextual bandits. Current offline-policy learning algorithms are mostly based on inverse propensity score (IPS) weighting requiring the logging policy to have \emph{full support} i.e. a non-zero probability for any context/action of the evaluation policy. However, many real-world systems do not guarantee such logging policies, especially when the action space is large and many actions have poor or missing rewards. With such \emph{support deficiency}, the offline learning fails to find optimal policies. We propose a novel approach that uses a hybrid of offline learning with online exploration. The online exploration is used to explore unsupported actions in the logged data whilst offline learning is used to exploit supported actions from the logged data avoiding unnecessary explorations. Our approach determines an optimal policy with theoretical guarantees using the minimal number of online explorations. We demonstrate our algorithms' effectiveness empirically on a diverse collection of datasets.

Bayesian Optimistic Optimisation with Exponentially Decaying Regret

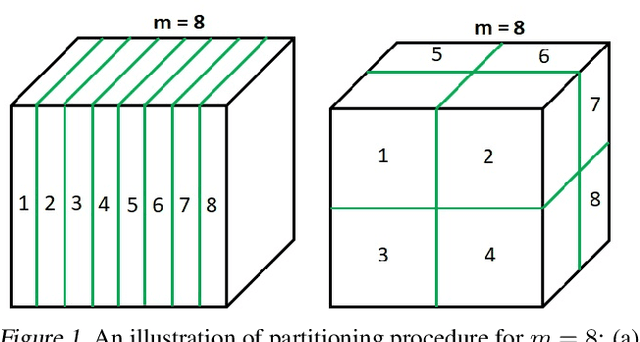
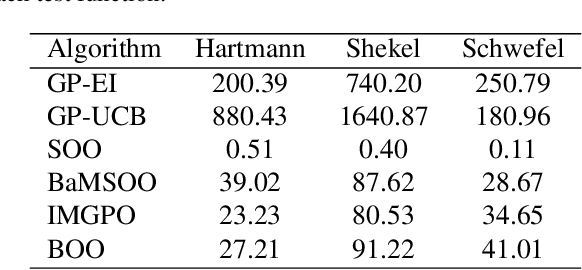
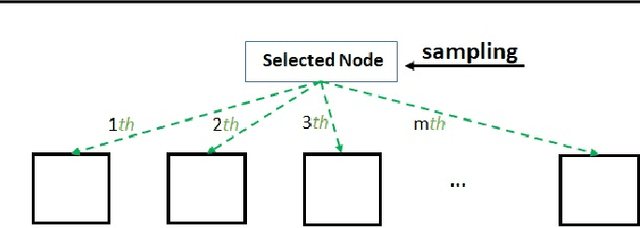
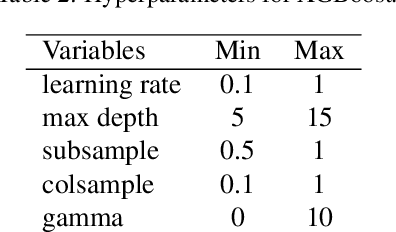
Bayesian optimisation (BO) is a well-known efficient algorithm for finding the global optimum of expensive, black-box functions. The current practical BO algorithms have regret bounds ranging from $\mathcal{O}(\frac{logN}{\sqrt{N}})$ to $\mathcal O(e^{-\sqrt{N}})$, where $N$ is the number of evaluations. This paper explores the possibility of improving the regret bound in the noiseless setting by intertwining concepts from BO and tree-based optimistic optimisation which are based on partitioning the search space. We propose the BOO algorithm, a first practical approach which can achieve an exponential regret bound with order $\mathcal O(N^{-\sqrt{N}})$ under the assumption that the objective function is sampled from a Gaussian process with a Mat\'ern kernel with smoothness parameter $\nu > 4 +\frac{D}{2}$, where $D$ is the number of dimensions. We perform experiments on optimisation of various synthetic functions and machine learning hyperparameter tuning tasks and show that our algorithm outperforms baselines.

On Finite-Sample Analysis of Offline Reinforcement Learning with Deep ReLU Networks

This paper studies the statistical theory of offline reinforcement learning with deep ReLU networks. We consider the off-policy evaluation (OPE) problem where the goal is to estimate the expected discounted reward of a target policy given the logged data generated by unknown behaviour policies. We study a regression-based fitted Q evaluation (FQE) method using deep ReLU networks and characterize a finite-sample bound on the estimation error of this method under mild assumptions. The prior works in OPE with either general function approximation or deep ReLU networks ignore the data-dependent structure in the algorithm, dodging the technical bottleneck of OPE, while requiring a rather restricted regularity assumption. In this work, we overcome these limitations and provide a comprehensive analysis of OPE with deep ReLU networks. In particular, we precisely quantify how the distribution shift of the offline data, the dimension of the input space, and the regularity of the system control the OPE estimation error. Consequently, we provide insights into the interplay between offline reinforcement learning and deep learning.

Sub-linear Regret Bounds for Bayesian Optimisation in Unknown Search Spaces

Bayesian optimisation is a popular method for efficient optimisation of expensive black-box functions. Traditionally, BO assumes that the search space is known. However, in many problems, this assumption does not hold. To this end, we propose a novel BO algorithm which expands (and shifts) the search space over iterations based on controlling the expansion rate thought a hyperharmonic series. Further, we propose another variant of our algorithm that scales to high dimensions. We show theoretically that for both our algorithms, the cumulative regret grows at sub-linear rates. Our experiments with synthetic and real-world optimisation tasks demonstrate the superiority of our algorithms over the current state-of-the-art methods for Bayesian optimisation in unknown search space.

Trading Convergence Rate with Computational Budget in High Dimensional Bayesian Optimization

Scaling Bayesian optimisation (BO) to high-dimensional search spaces is a active and open research problems particularly when no assumptions are made on function structure. The main reason is that at each iteration, BO requires to find global maximisation of acquisition function, which itself is a non-convex optimization problem in the original search space. With growing dimensions, the computational budget for this maximisation gets increasingly short leading to inaccurate solution of the maximisation. This inaccuracy adversely affects both the convergence and the efficiency of BO. We propose a novel approach where the acquisition function only requires maximisation on a discrete set of low dimensional subspaces embedded in the original high-dimensional search space. Our method is free of any low dimensional structure assumption on the function unlike many recent high-dimensional BO methods. Optimising acquisition function in low dimensional subspaces allows our method to obtain accurate solutions within limited computational budget. We show that in spite of this convenience, our algorithm remains convergent. In particular, cumulative regret of our algorithm only grows sub-linearly with the number of iterations. More importantly, as evident from our regret bounds, our algorithm provides a way to trade the convergence rate with the number of subspaces used in the optimisation. Finally, when the number of subspaces is "sufficiently large", our algorithm's cumulative regret is at most $\mathcal{O}^{*}(\sqrt{T\gamma_T})$ as opposed to $\mathcal{O}^{*}(\sqrt{DT\gamma_T})$ for the GP-UCB of Srinivas et al. (2012), reducing a crucial factor $\sqrt{D}$ where $D$ being the dimensional number of input space.

Bayesian Optimization with Unknown Search Space

Applying Bayesian optimization in problems wherein the search space is unknown is challenging. To address this problem, we propose a systematic volume expansion strategy for the Bayesian optimization. We devise a strategy to guarantee that in iterative expansions of the search space, our method can find a point whose function value within epsilon of the objective function maximum. Without the need to specify any parameters, our algorithm automatically triggers a minimal expansion required iteratively. We derive analytic expressions for when to trigger the expansion and by how much to expand. We also provide theoretical analysis to show that our method achieves epsilon-accuracy after a finite number of iterations. We demonstrate our method on both benchmark test functions and machine learning hyper-parameter tuning tasks and demonstrate that our method outperforms baselines.