On Maintaining Linear Convergence of Distributed Learning and Optimization under Limited Communication

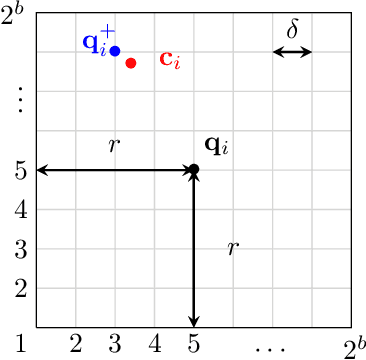
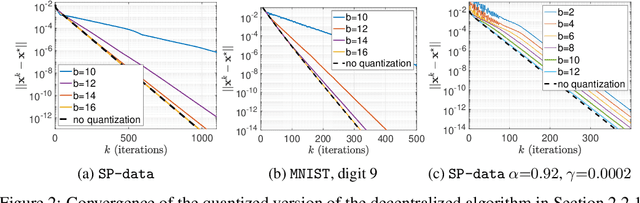
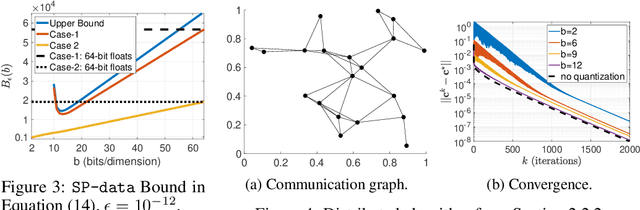
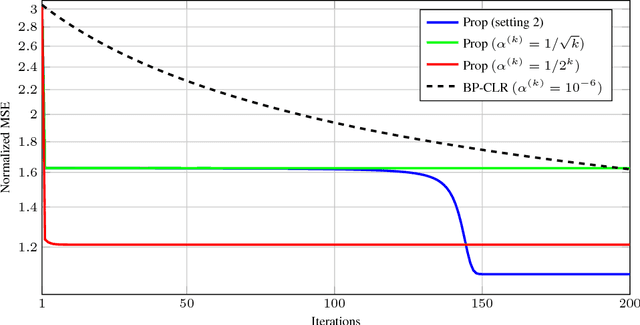
In parallel and distributed machine learning multiple nodes or processors coordinate to solve large problems. To do this, nodes need to compress important algorithm information to bits so it can be communicated. The goal of this paper is to explore how we can maintain the convergence of distributed algorithms under such compression. In particular, we consider a general class of linearly convergent parallel/distributed algorithms and illustrate how we can design quantizers compressing the communicated information to few bits while still preserving the linear convergence. We illustrate our results on learning algorithms using different communication structures, such as decentralized algorithms where a single master coordinates information from many workers and fully distributed algorithms where only neighbors in a communication graph can communicate. We also numerically implement our results in distributed learning on smartphones using real-world data.

Learning Kolmogorov Models for Binary Random Variables

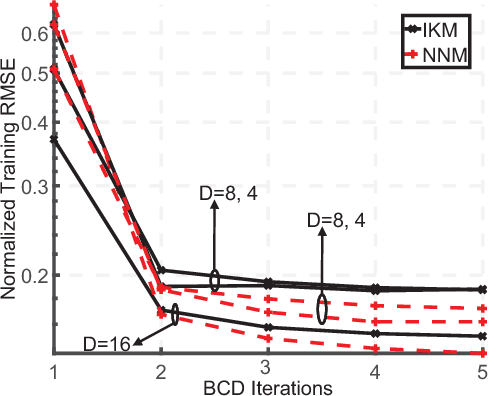
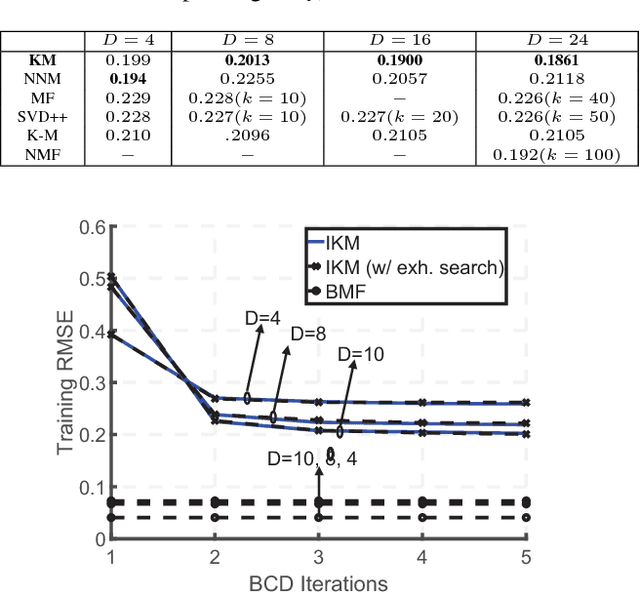
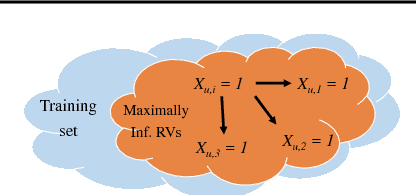
We summarize our recent findings, where we proposed a framework for learning a Kolmogorov model, for a collection of binary random variables. More specifically, we derive conditions that link outcomes of specific random variables, and extract valuable relations from the data. We also propose an algorithm for computing the model and show its first-order optimality, despite the combinatorial nature of the learning problem. We apply the proposed algorithm to recommendation systems, although it is applicable to other scenarios. We believe that the work is a significant step toward interpretable machine learning.

A Unified Framework for Training Neural Networks

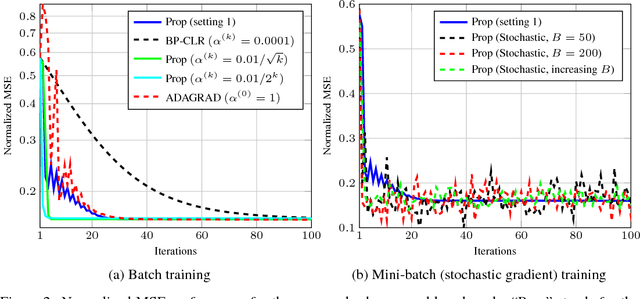
The lack of mathematical tractability of Deep Neural Networks (DNNs) has hindered progress towards having a unified convergence analysis of training algorithms, in the general setting. We propose a unified optimization framework for training different types of DNNs, and establish its convergence for arbitrary loss, activation, and regularization functions, assumed to be smooth. We show that framework generalizes well-known first- and second-order training methods, and thus allows us to show the convergence of these methods for various DNN architectures and learning tasks, as a special case of our approach. We discuss some of its applications in training various DNN architectures (e.g., feed-forward, convolutional, linear networks), to regression and classification tasks.

Analytical and Learning-Based Spectrum Sensing Time Optimization in Cognitive Radio Systems

Powerful spectrum sensing schemes enable cognitive radios (CRs) to find transmission opportunities in spectral resources allocated exclusively to the primary users. In this paper, maximizing the average throughput of a secondary user by optimizing its spectrum sensing time is formulated assuming that a prior knowledge of the presence and absence probabilities of the primary users is available. The energy consumed for finding a transmission opportunity is evaluated and a discussion on the impact of the number of the primary users on the secondary user throughput and consumed energy is presented. In order to avoid the challenges associated with the analytical method, as a second solution, a systematic neural network-based sensing time optimization approach is also proposed in this paper. The proposed adaptive scheme is able to find the optimum value of the channel sensing time without any prior knowledge or assumption about the wireless environment. The structure, performance, and cooperation of the artificial neural networks used in the proposed method are disclosed in detail and a set of illustrative simulation results is presented to validate the analytical results as well as the performance of the proposed learning-based optimization scheme.