On Maintaining Linear Convergence of Distributed Learning and Optimization under Limited Communication

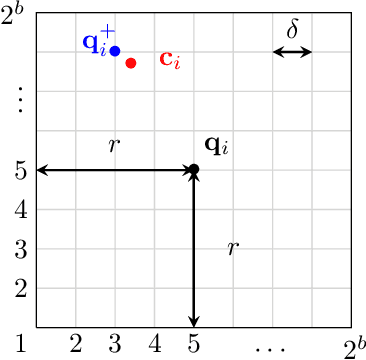
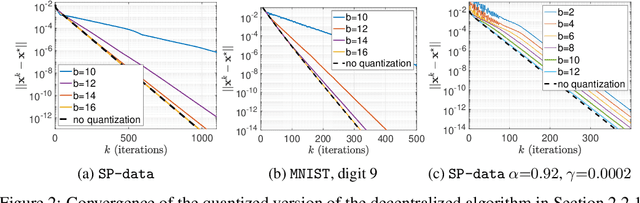
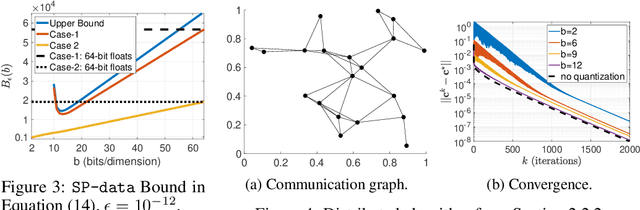
In parallel and distributed machine learning multiple nodes or processors coordinate to solve large problems. To do this, nodes need to compress important algorithm information to bits so it can be communicated. The goal of this paper is to explore how we can maintain the convergence of distributed algorithms under such compression. In particular, we consider a general class of linearly convergent parallel/distributed algorithms and illustrate how we can design quantizers compressing the communicated information to few bits while still preserving the linear convergence. We illustrate our results on learning algorithms using different communication structures, such as decentralized algorithms where a single master coordinates information from many workers and fully distributed algorithms where only neighbors in a communication graph can communicate. We also numerically implement our results in distributed learning on smartphones using real-world data.