A Unified Framework for Training Neural Networks
Paper and Code
May 23, 2018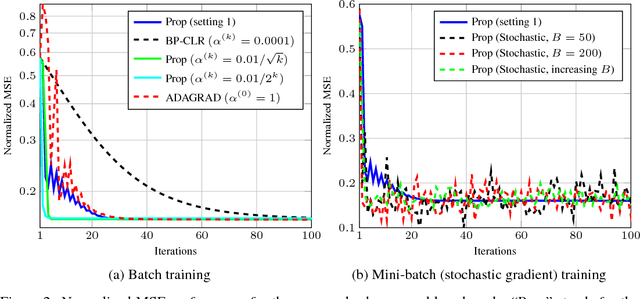
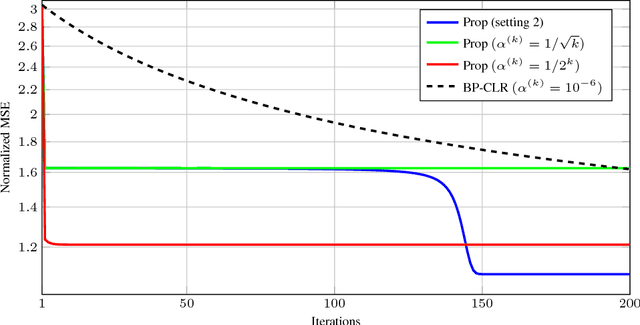
The lack of mathematical tractability of Deep Neural Networks (DNNs) has hindered progress towards having a unified convergence analysis of training algorithms, in the general setting. We propose a unified optimization framework for training different types of DNNs, and establish its convergence for arbitrary loss, activation, and regularization functions, assumed to be smooth. We show that framework generalizes well-known first- and second-order training methods, and thus allows us to show the convergence of these methods for various DNN architectures and learning tasks, as a special case of our approach. We discuss some of its applications in training various DNN architectures (e.g., feed-forward, convolutional, linear networks), to regression and classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge