SRLCG: Self-Rectified Large-Scale Code Generation with Multidimensional Chain-of-Thought and Dynamic Backtracking

Large language models (LLMs) have revolutionized code generation, significantly enhancing developer productivity. However, for a vast number of users with minimal coding knowledge, LLMs provide little support, as they primarily generate isolated code snippets rather than complete, large-scale project code. Without coding expertise, these users struggle to interpret, modify, and iteratively refine the outputs of LLMs, making it impossible to assemble a complete project. To address this issue, we propose Self-Rectified Large-Scale Code Generator (SRLCG), a framework that generates complete multi-file project code from a single prompt. SRLCG employs a novel multidimensional chain-of-thought (CoT) and self-rectification to guide LLMs in generating correct and robust code files, then integrates them into a complete and coherent project using our proposed dynamic backtracking algorithm. Experimental results show that SRLCG generates code 15x longer than DeepSeek-V3, 16x longer than GPT-4, and at least 10x longer than other leading CoT-based baselines. Furthermore, they confirm its improved correctness, robustness, and performance compared to baselines in large-scale code generation.

MOBA: A multi-objective bounded-abstention model for two-class cost-sensitive problems

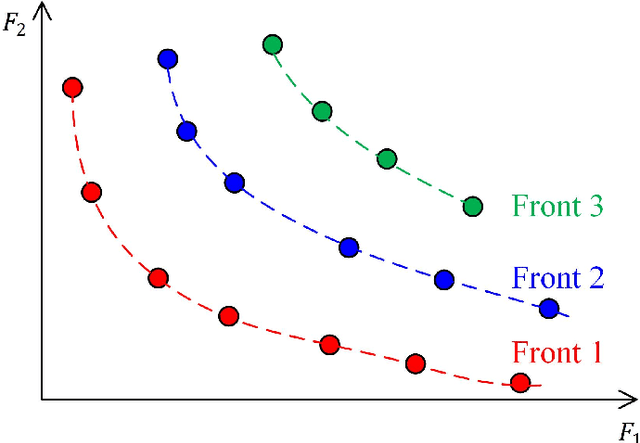
Abstaining classifiers have been widely used in cost-sensitive applications to avoid ambiguous classification and reduce the cost of misclassification. Previous abstaining classification models rely on cost information, such as a cost matrix or cost ratio. However, it is difficult to obtain or estimate costs in practical applications. Furthermore, these abstention models are typically restricted to a single optimization metric, which may not be the expected indicator when evaluating classification performance. To overcome such problems, a multi-objective bounded-abstention (MOBA) model is proposed to optimize essential metrics. Specifically, the MOBA model minimizes the error rate of each class under class-dependent abstention constraints. The MOBA model is then solved using the non-dominated sorting genetic algorithm II, which is a popular evolutionary multi-objective optimization algorithm. A set of Pareto-optimal solutions will be generated and the best one can be selected according to provided conditions (whether costs are known) or performance demands (e.g., obtaining a high accuracy, F-measure, and etc). Hence, the MOBA model is robust towards variations in the conditions and requirements. Compared to state-of-the-art abstention models, MOBA achieves lower expected costs when cost information is considered, and better performance-abstention trade-offs when it is not.

Abstaining Classification When Error Costs are Unequal and Unknown

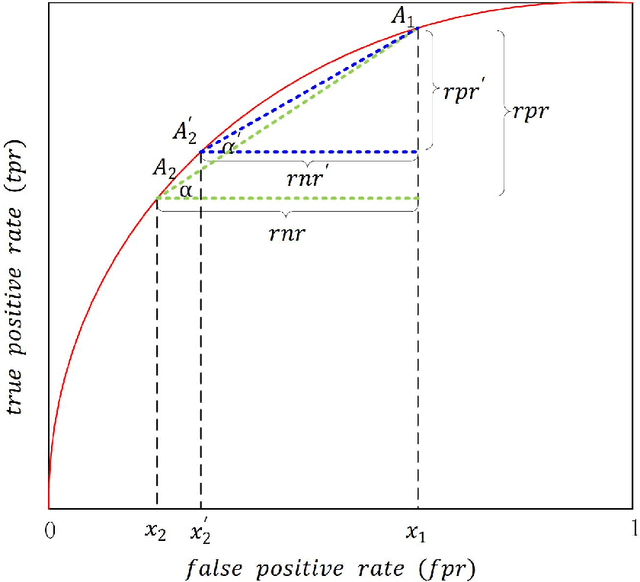
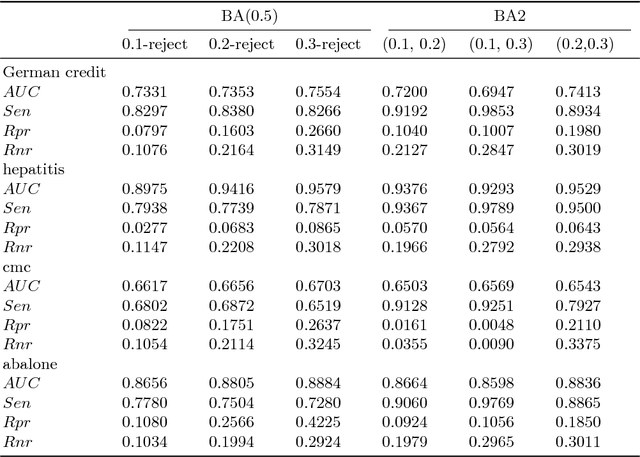
Abstaining classificaiton aims to reject to classify the easily misclassified examples, so it is an effective approach to increase the clasificaiton reliability and reduce the misclassification risk in the cost-sensitive applications. In such applications, different types of errors (false positive or false negative) usaully have unequal costs. And the error costs, which depend on specific applications, are usually unknown. However, current abstaining classification methods either do not distinguish the error types, or they need the cost information of misclassification and rejection, which are realized in the framework of cost-sensitive learning. In this paper, we propose a bounded-abstention method with two constraints of reject rates (BA2), which performs abstaining classification when error costs are unequal and unknown. BA2 aims to obtain the optimal area under the ROC curve (AUC) by constraining the reject rates of the positive and negative classes respectively. Specifically, we construct the receiver operating characteristic (ROC) curve, and stepwise search the optimal reject thresholds from both ends of the curve, untill the two constraints are satisfied. Experimental results show that BA2 obtains higher AUC and lower total cost than the state-of-the-art abstaining classification methods. Meanwhile, BA2 achieves controllable reject rates of the positive and negative classes.