Abstaining Classification When Error Costs are Unequal and Unknown
Paper and Code
Jul 25, 2018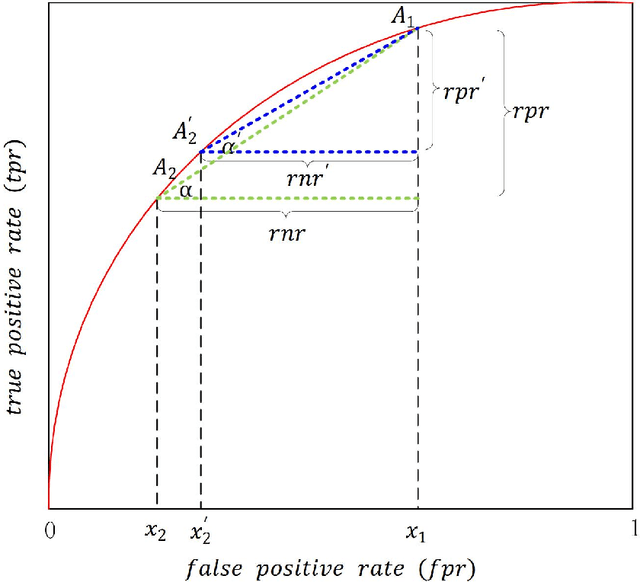
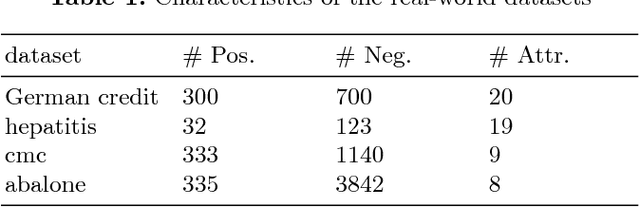
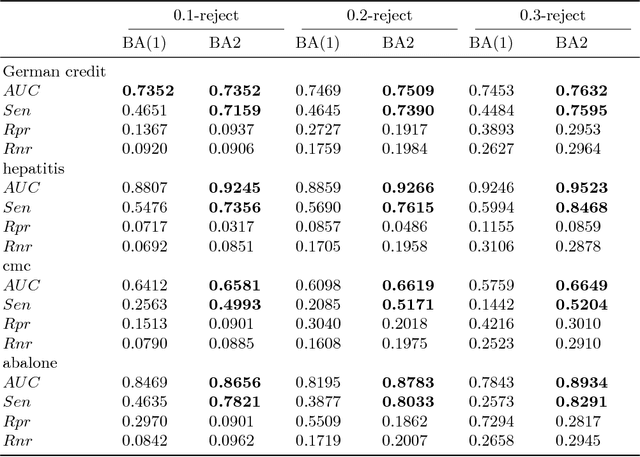
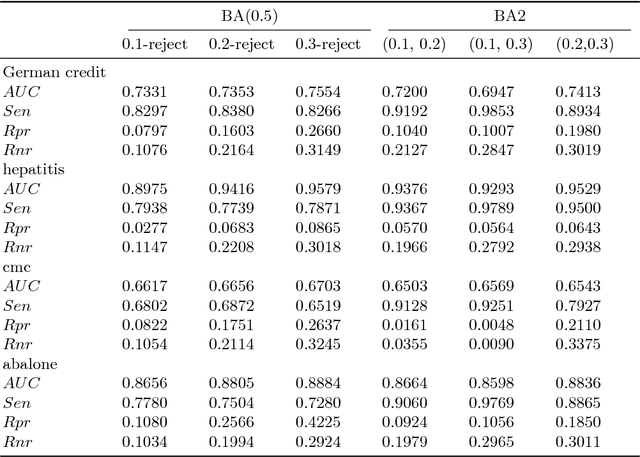
Abstaining classificaiton aims to reject to classify the easily misclassified examples, so it is an effective approach to increase the clasificaiton reliability and reduce the misclassification risk in the cost-sensitive applications. In such applications, different types of errors (false positive or false negative) usaully have unequal costs. And the error costs, which depend on specific applications, are usually unknown. However, current abstaining classification methods either do not distinguish the error types, or they need the cost information of misclassification and rejection, which are realized in the framework of cost-sensitive learning. In this paper, we propose a bounded-abstention method with two constraints of reject rates (BA2), which performs abstaining classification when error costs are unequal and unknown. BA2 aims to obtain the optimal area under the ROC curve (AUC) by constraining the reject rates of the positive and negative classes respectively. Specifically, we construct the receiver operating characteristic (ROC) curve, and stepwise search the optimal reject thresholds from both ends of the curve, untill the two constraints are satisfied. Experimental results show that BA2 obtains higher AUC and lower total cost than the state-of-the-art abstaining classification methods. Meanwhile, BA2 achieves controllable reject rates of the positive and negative classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge