Sharp Matrix Empirical Bernstein Inequalities

We present two sharp empirical Bernstein inequalities for symmetric random matrices with bounded eigenvalues. By sharp, we mean that both inequalities adapt to the unknown variance in a tight manner: the deviation captured by the first-order $1/\sqrt{n}$ term asymptotically matches the matrix Bernstein inequality exactly, including constants, the latter requiring knowledge of the variance. Our first inequality holds for the sample mean of independent matrices, and our second inequality holds for a mean estimator under martingale dependence at stopping times.

Matrix Supermartingales and Randomized Matrix Concentration Inequalities

We present new concentration inequalities for either martingale dependent or exchangeable random symmetric matrices under a variety of tail conditions, encompassing standard Chernoff bounds to self-normalized heavy-tailed settings. These inequalities are often randomized in a way that renders them strictly tighter than existing deterministic results in the literature, are typically expressed in the Loewner order, and are sometimes valid at arbitrary data-dependent stopping times. Along the way, we explore the theory of matrix supermartingales and maximal inequalities, potentially of independent interest.

Time-Uniform Confidence Spheres for Means of Random Vectors

We derive and study time-uniform confidence spheres - termed confidence sphere sequences (CSSs) - which contain the mean of random vectors with high probability simultaneously across all sample sizes. Inspired by the original work of Catoni and Giulini, we unify and extend their analysis to cover both the sequential setting and to handle a variety of distributional assumptions. More concretely, our results include an empirical-Bernstein CSS for bounded random vectors (resulting in a novel empirical-Bernstein confidence interval), a CSS for sub-$\psi$ random vectors, and a CSS for heavy-tailed random vectors based on a sequentially valid Catoni-Giulini estimator. Finally, we provide a version of our empirical-Bernstein CSS that is robust to contamination by Huber noise.

Anytime-valid t-tests and confidence sequences for Gaussian means with unknown variance

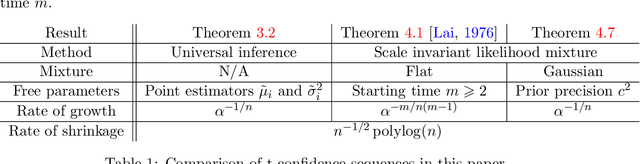
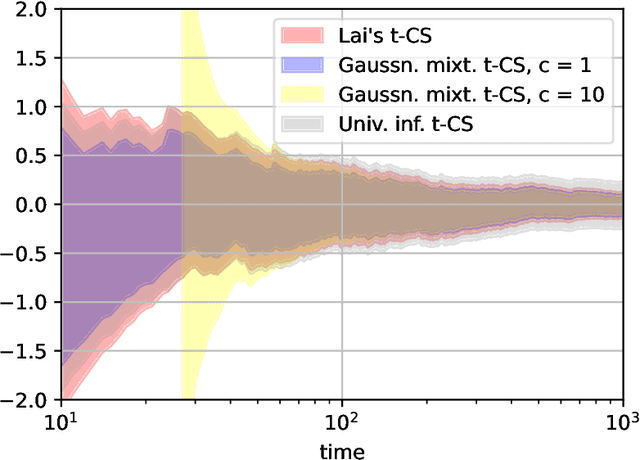
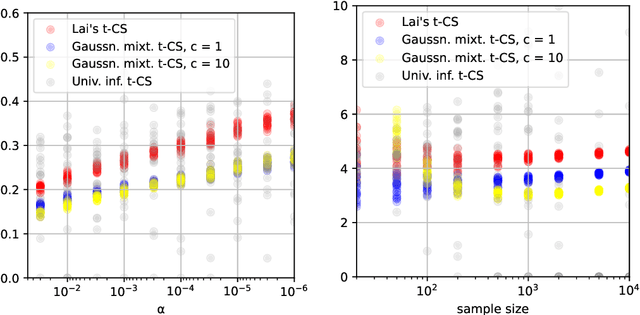
In 1976, Lai constructed a nontrivial confidence sequence for the mean $\mu$ of a Gaussian distribution with unknown variance $\sigma$. Curiously, he employed both an improper (right Haar) mixture over $\sigma$ and an improper (flat) mixture over $\mu$. Here, we elaborate carefully on the details of his construction, which use generalized nonintegrable martingales and an extended Ville's inequality. While this does yield a sequential t-test, it does not yield an ``e-process'' (due to the nonintegrability of his martingale). In this paper, we develop two new e-processes and confidence sequences for the same setting: one is a test martingale in a reduced filtration, while the other is an e-process in the canonical data filtration. These are respectively obtained by swapping Lai's flat mixture for a Gaussian mixture, and swapping the right Haar mixture over $\sigma$ with the maximum likelihood estimate under the null, as done in universal inference. We also analyze the width of resulting confidence sequences, which have a curious dependence on the error probability $\alpha$. Numerical experiments are provided along the way to compare and contrast the various approaches.

Dynamic Visual Prompt Tuning for Parameter Efficient Transfer Learning

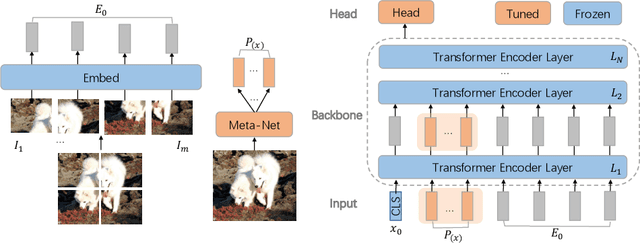
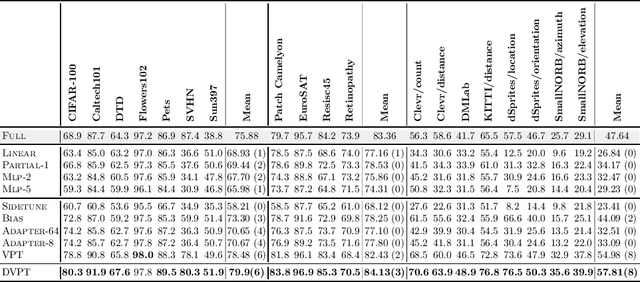
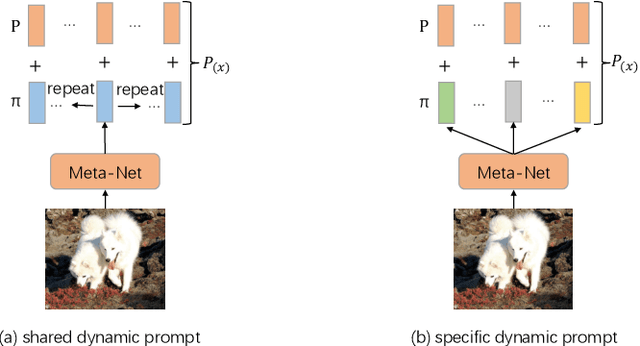
Parameter efficient transfer learning (PETL) is an emerging research spot that aims to adapt large-scale pre-trained models to downstream tasks. Recent advances have achieved great success in saving storage and computation costs. However, these methods do not take into account instance-specific visual clues for visual tasks. In this paper, we propose a Dynamic Visual Prompt Tuning framework (DVPT), which can generate a dynamic instance-wise token for each image. In this way, it can capture the unique visual feature of each image, which can be more suitable for downstream visual tasks. We designed a Meta-Net module that can generate learnable prompts based on each image, thereby capturing dynamic instance-wise visual features. Extensive experiments on a wide range of downstream recognition tasks show that DVPT achieves superior performance than other PETL methods. More importantly, DVPT even outperforms full fine-tuning on 17 out of 19 downstream tasks while maintaining high parameter efficiency. Our code will be released soon.

The extended Ville's inequality for nonintegrable nonnegative supermartingales

Following initial work by Robbins, we rigorously present an extended theory of nonnegative supermartingales, requiring neither integrability nor finiteness. In particular, we derive a key maximal inequality foreshadowed by Robbins, which we call the extended Ville's inequality, that strengthens the classical Ville's inequality (for integrable nonnegative supermartingales), and also applies to our nonintegrable setting. We derive an extension of the method of mixtures, which applies to $\sigma$-finite mixtures of our extended nonnegative supermartingales. We present some implications of our theory for sequential statistics, such as the use of improper mixtures (priors) in deriving nonparametric confidence sequences and (extended) e-processes.

Learning Spatial-Temporal Implicit Neural Representations for Event-Guided Video Super-Resolution

Event cameras sense the intensity changes asynchronously and produce event streams with high dynamic range and low latency. This has inspired research endeavors utilizing events to guide the challenging video superresolution (VSR) task. In this paper, we make the first attempt to address a novel problem of achieving VSR at random scales by taking advantages of the high temporal resolution property of events. This is hampered by the difficulties of representing the spatial-temporal information of events when guiding VSR. To this end, we propose a novel framework that incorporates the spatial-temporal interpolation of events to VSR in a unified framework. Our key idea is to learn implicit neural representations from queried spatial-temporal coordinates and features from both RGB frames and events. Our method contains three parts. Specifically, the Spatial-Temporal Fusion (STF) module first learns the 3D features from events and RGB frames. Then, the Temporal Filter (TF) module unlocks more explicit motion information from the events near the queried timestamp and generates the 2D features. Lastly, the SpatialTemporal Implicit Representation (STIR) module recovers the SR frame in arbitrary resolutions from the outputs of these two modules. In addition, we collect a real-world dataset with spatially aligned events and RGB frames. Extensive experiments show that our method significantly surpasses the prior-arts and achieves VSR with random scales, e.g., 6.5. Code and dataset are available at https: //vlis2022.github.io/cvpr23/egvsr.

A unified recipe for deriving PAC-Bayes bounds

We present a unified framework for deriving PAC-Bayesian generalization bounds. Unlike most previous literature on this topic, our bounds are anytime-valid (i.e., time-uniform), meaning that they hold at all stopping times, not only for a fixed sample size. Our approach combines four tools in the following order: (a) nonnegative supermartingales or reverse submartingales, (b) the method of mixtures, (c) the Donsker-Varadhan formula (or other convex duality principles), and (d) Ville's inequality. Our main result is a PAC-Bayes theorem which holds for a wide class of discrete stochastic processes. We show how this result implies time-uniform versions of well-known classical PAC-Bayes bounds, such as those of Seeger, McAllester, Maurer, and Catoni, in addition to many recent bounds. We also present several novel bounds. Our framework also enables us to relax traditional assumptions; in particular, we consider nonstationary loss functions and non-i.i.d. data. In sum, we unify the derivation of past bounds and ease the search for future bounds: one may simply check if our supermartingale or submartingale conditions are met and, if so, be guaranteed a (time-uniform) PAC-Bayes bound.

Huber-Robust Confidence Sequences

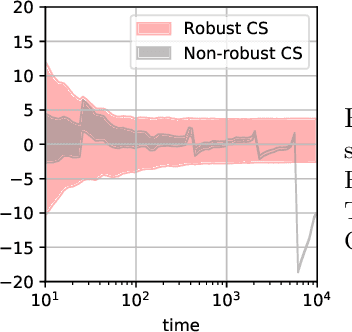
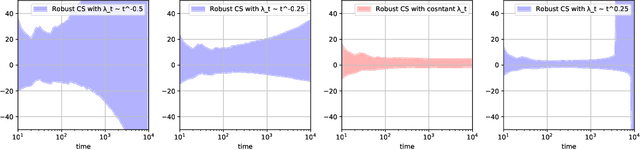
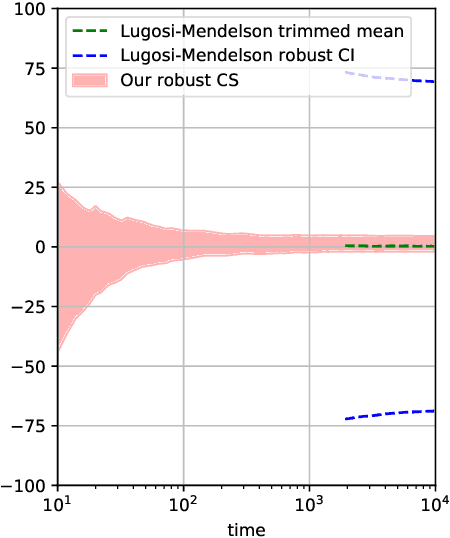
Confidence sequences are confidence intervals that can be sequentially tracked, and are valid at arbitrary data-dependent stopping times. This paper presents confidence sequences for a univariate mean of an unknown distribution with a known upper bound on the p-th central moment (p > 1), but allowing for (at most) {\epsilon} fraction of arbitrary distribution corruption, as in Huber's contamination model. We do this by designing new robust exponential supermartingales, and show that the resulting confidence sequences attain the optimal width achieved in the nonsequential setting. Perhaps surprisingly, the constant margin between our sequential result and the lower bound is smaller than even fixed-time robust confidence intervals based on the trimmed mean, for example. Since confidence sequences are a common tool used within A/B/n testing and bandits, these results open the door to sequential experimentation that is robust to outliers and adversarial corruptions.

Convergence Rates of Stochastic Gradient Descent under Infinite Noise Variance

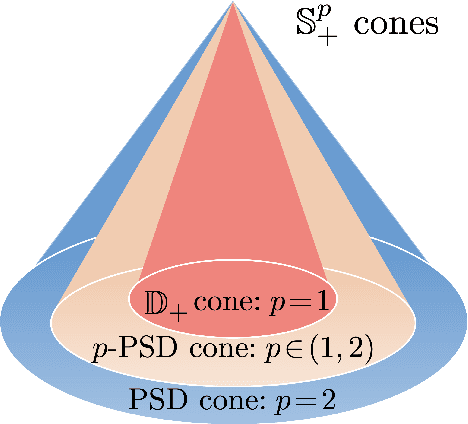
Recent studies have provided both empirical and theoretical evidence illustrating that heavy tails can emerge in stochastic gradient descent (SGD) in various scenarios. Such heavy tails potentially result in iterates with diverging variance, which hinders the use of conventional convergence analysis techniques that rely on the existence of the second-order moments. In this paper, we provide convergence guarantees for SGD under a state-dependent and heavy-tailed noise with a potentially infinite variance, for a class of strongly convex objectives. In the case where the $p$-th moment of the noise exists for some $p\in [1,2)$, we first identify a condition on the Hessian, coined '$p$-positive (semi-)definiteness', that leads to an interesting interpolation between positive semi-definite matrices ($p=2$) and diagonally dominant matrices with non-negative diagonal entries ($p=1$). Under this condition, we then provide a convergence rate for the distance to the global optimum in $L^p$. Furthermore, we provide a generalized central limit theorem, which shows that the properly scaled Polyak-Ruppert averaging converges weakly to a multivariate $\alpha$-stable random vector. Our results indicate that even under heavy-tailed noise with infinite variance, SGD can converge to the global optimum without necessitating any modification neither to the loss function or to the algorithm itself, as typically required in robust statistics. We demonstrate the implications of our results to applications such as linear regression and generalized linear models subject to heavy-tailed data.