Anytime-valid t-tests and confidence sequences for Gaussian means with unknown variance

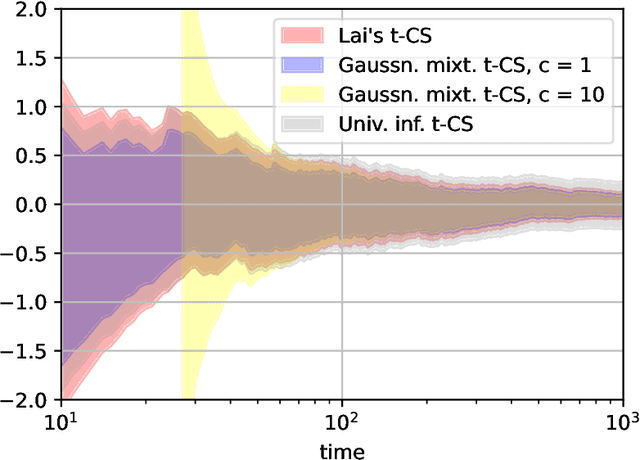
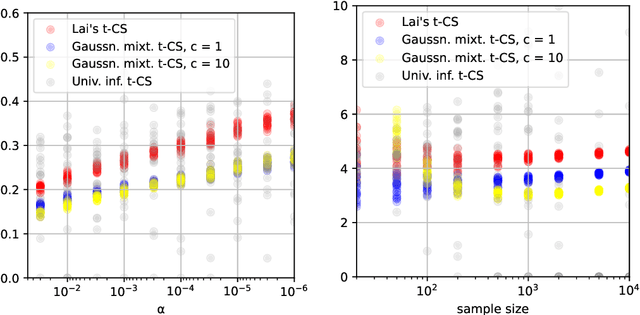
In 1976, Lai constructed a nontrivial confidence sequence for the mean $\mu$ of a Gaussian distribution with unknown variance $\sigma$. Curiously, he employed both an improper (right Haar) mixture over $\sigma$ and an improper (flat) mixture over $\mu$. Here, we elaborate carefully on the details of his construction, which use generalized nonintegrable martingales and an extended Ville's inequality. While this does yield a sequential t-test, it does not yield an ``e-process'' (due to the nonintegrability of his martingale). In this paper, we develop two new e-processes and confidence sequences for the same setting: one is a test martingale in a reduced filtration, while the other is an e-process in the canonical data filtration. These are respectively obtained by swapping Lai's flat mixture for a Gaussian mixture, and swapping the right Haar mixture over $\sigma$ with the maximum likelihood estimate under the null, as done in universal inference. We also analyze the width of resulting confidence sequences, which have a curious dependence on the error probability $\alpha$. Numerical experiments are provided along the way to compare and contrast the various approaches.