A Robot Kinematics Model Estimation Using Inertial Sensors for On-Site Building Robotics

In order to make robots more useful in a variety of environments, they need to be highly portable so that they can be transported to wherever they are needed, and highly storable so that they can be stored when not in use. We propose "on-site robotics", which uses parts procured at the location where the robot will be active, and propose a new solution to the problem of portability and storability. In this paper, as a proof of concept for on-site robotics, we describe a method for estimating the kinematic model of a robot by using inertial measurement units (IMU) sensor module on rigid links, estimating the relative orientation between modules from angular velocity, and estimating the relative position from the measurement of centrifugal force. At the end of this paper, as an evaluation for this method, we present an experiment in which a robot made up of wooden sticks reaches a target position. In this experiment, even if the combination of the links is changed, the robot is able to reach the target position again immediately after estimation, showing that it can operate even after being reassembled. Our implementation is available on https://github.com/hiroya1224/urdf_estimation_with_imus .

A Planar-Symmetric SO(3) Representation for Learning Grasp Detection

Planar-symmetric hands, such as parallel grippers, are widely adopted in both research and industrial fields. Their symmetry, however, introduces ambiguity and discontinuity in the SO(3) representation, which hinders both the training and inference of neural-network-based grasp detectors. We propose a novel SO(3) representation that can parametrize a pair of planar-symmetric poses with a single parameter set by leveraging the 2D Bingham distribution. We also detail a grasp detector based on our representation, which provides a more consistent rotation output. An intensive evaluation with multiple grippers and objects in both the simulation and the real world quantitatively shows our approach's contribution.

Online Estimation of Self-Body Deflection With Various Sensor Data Based on Directional Statistics

In this paper, we propose a method for online estimation of the robot's posture. Our method uses von Mises and Bingham distributions as probability distributions of joint angles and 3D orientation, which are used in directional statistics. We constructed a particle filter using these distributions and configured a system to estimate the robot's posture from various sensor information (e.g., joint encoders, IMU sensors, and cameras). Furthermore, unlike tangent space approximations, these distributions can handle global features and represent sensor characteristics as observation noises. As an application, we show that the yaw drift of a 6-axis IMU sensor can be represented probabilistically to prevent adverse effects on attitude estimation. For the estimation, we used an approximate model that assumes the actual robot posture can be reproduced by correcting the joint angles of a rigid body model. In the experiment part, we tested the estimator's effectiveness by examining that the joint angles generated with the approximate model can be estimated using the link pose of the same model. We then applied the estimator to the actual robot and confirmed that the gripper position could be estimated, thereby verifying the validity of the approximate model in our situation.

A Probabilistic Rotation Representation for Symmetric Shapes With an Efficiently Computable Bingham Loss Function

In recent years, a deep learning framework has been widely used for object pose estimation. While quaternion is a common choice for rotation representation, it cannot represent the ambiguity of the observation. In order to handle the ambiguity, the Bingham distribution is one promising solution. However, it requires complicated calculation when yielding the negative log-likelihood (NLL) loss. An alternative easy-to-implement loss function has been proposed to avoid complex computations but has difficulty expressing symmetric distribution. In this paper, we introduce a fast-computable and easy-to-implement NLL loss function for Bingham distribution. We also create the inference network and show that our loss function can capture the symmetric property of target objects from their point clouds.

Probabilistic Rotation Representation With an Efficiently Computable Bingham Loss Function and Its Application to Pose Estimation

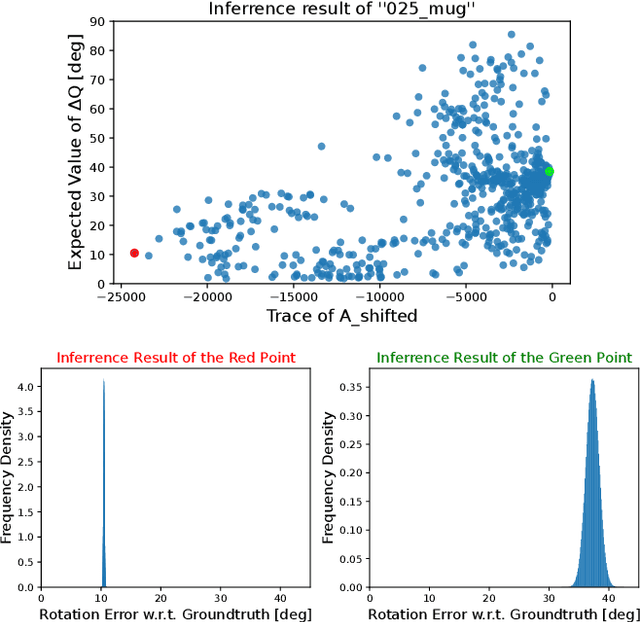
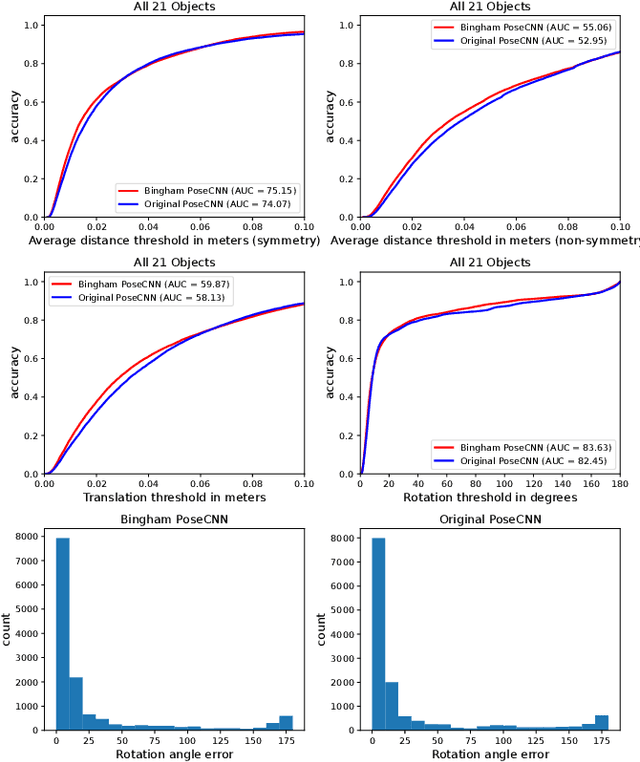
In recent years, a deep learning framework has been widely used for object pose estimation. While quaternion is a common choice for rotation representation of 6D pose, it cannot represent an uncertainty of the observation. In order to handle the uncertainty, Bingham distribution is one promising solution because this has suitable features, such as a smooth representation over SO(3), in addition to the ambiguity representation. However, it requires the complex computation of the normalizing constants. This is the bottleneck of loss computation in training neural networks based on Bingham representation. As such, we propose a fast-computable and easy-to-implement loss function for Bingham distribution. We also show not only to examine the parametrization of Bingham distribution but also an application based on our loss function.