First numerical observation of the Berezinskii-Kosterlitz-Thouless transition in language models

Several power-law critical properties involving different statistics in natural languages -- reminiscent of scaling properties of physical systems at or near phase transitions -- have been documented for decades. The recent rise of large language models (LLMs) has added further evidence and excitement by providing intriguing similarities with notions in physics such as scaling laws and emergent abilities. However, specific instances of classes of generative language models that exhibit phase transitions, as understood by the statistical physics community, are lacking. In this work, inspired by the one-dimensional Potts model in statistical physics we construct a simple probabilistic language model that falls under the class of context sensitive grammars (CSG), and numerically demonstrate an unambiguous phase transition in the framework of a natural language model. We explicitly show that a precisely defined order parameter -- that captures symbol frequency biases in the sentences generated by the language model -- changes from strictly 0 to a strictly nonzero value (in the infinite-length limit of sentences), implying a mathematical singularity arising when tuning the parameter of the stochastic language model we consider. Furthermore, we identify the phase transition as a variant of the Berezinskii-Kosterlitz-Thouless (BKT) transition, which is known to exhibit critical properties not only at the transition point but also in the entire phase. This finding leads to the possibility that critical properties in natural languages may not require careful fine-tuning nor self-organized criticality, but is generically explained by the underlying connection between language structures and the BKT phases.

Quantum natural gradient without monotonicity

Natural gradient (NG) is an information-geometric optimization method that plays a crucial role, especially in the estimation of parameters for machine learning models like neural networks. To apply NG to quantum systems, the quantum natural gradient (QNG) was introduced and utilized for noisy intermediate-scale devices. Additionally, a mathematically equivalent approach to QNG, known as the stochastic reconfiguration method, has been implemented to enhance the performance of quantum Monte Carlo methods. It is worth noting that these methods are based on the symmetric logarithmic derivative (SLD) metric, which is one of the monotone metrics. So far, monotonicity has been believed to be a guiding principle to construct a geometry in physics. In this paper, we propose generalized QNG by removing the condition of monotonicity. Initially, we demonstrate that monotonicity is a crucial condition for conventional QNG to be optimal. Subsequently, we provide analytical and numerical evidence showing that non-monotone QNG outperforms conventional QNG based on the SLD metric in terms of convergence speed.

Information geometric bound on general chemical reaction networks

We investigate the dynamics of chemical reaction networks (CRNs) with the goal of deriving an upper bound on their reaction rates. This task is challenging due to the nonlinear nature and discrete structure inherent in CRNs. To address this, we employ an information geometric approach, using the natural gradient, to develop a nonlinear system that yields an upper bound for CRN dynamics. We validate our approach through numerical simulations, demonstrating faster convergence in a specific class of CRNs. This class is characterized by the number of chemicals, the maximum value of stoichiometric coefficients of the chemical reactions, and the number of reactions. We also compare our method to a conventional approach, showing that the latter cannot provide an upper bound on reaction rates of CRNs. While our study focuses on CRNs, the ubiquity of hypergraphs in fields from natural sciences to engineering suggests that our method may find broader applications, including in information science.

Quantum Advantage in Variational Bayes Inference

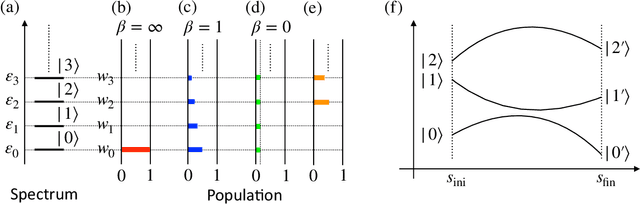
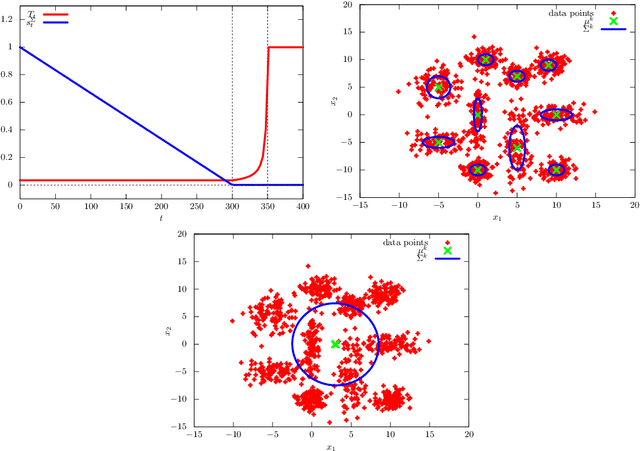
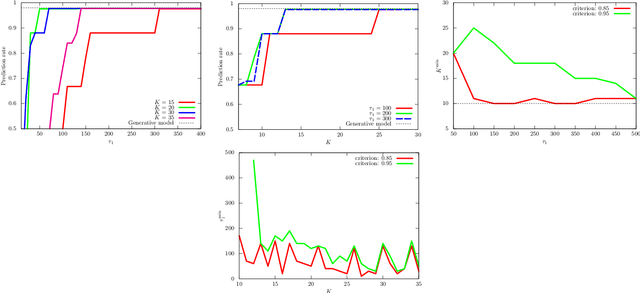
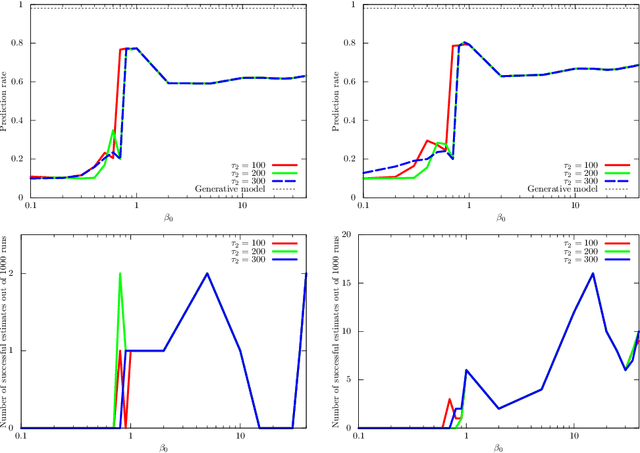
Variational Bayes (VB) inference algorithm is used widely to estimate both the parameters and the unobserved hidden variables in generative statistical models. The algorithm -- inspired by variational methods used in computational physics -- is iterative and can get easily stuck in local minima, even when classical techniques, such as deterministic annealing (DA), are used. We study a variational Bayes (VB) inference algorithm based on a non-traditional quantum annealing approach -- referred to as quantum annealing variational Bayes (QAVB) inference -- and show that there is indeed a quantum advantage to QAVB over its classical counterparts. In particular, we show that such better performance is rooted in key concepts from quantum mechanics: (i) the ground state of the Hamiltonian of a quantum system -- defined from the given variational Bayes (VB) problem -- corresponds to an optimal solution for the minimization problem of the variational free energy at very low temperatures; (ii) such a ground state can be achieved by a technique paralleling the quantum annealing process; and (iii) starting from this ground state, the optimal solution to the VB problem can be achieved by increasing the heat bath temperature to unity, and thereby avoiding local minima introduced by spontaneous symmetry breaking observed in classical physics based VB algorithms. We also show that the update equations of QAVB can be potentially implemented using $\lceil \log K \rceil$ qubits and $\mathcal{O} (K)$ operations per step. Thus, QAVB can match the time complexity of existing VB algorithms, while delivering higher performance.

Quantum Approximation of Normalized Schatten Norms and Applications to Learning

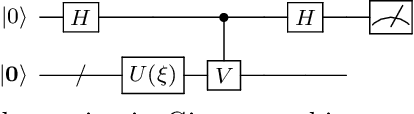
Efficient measures to determine similarity of quantum states, such as the fidelity metric, have been widely studied. In this paper, we address the problem of defining a similarity measure for quantum operations that can be \textit{efficiently estimated}. Given two quantum operations, $U_1$ and $U_2$, represented in their circuit forms, we first develop a quantum sampling circuit to estimate the normalized Schatten 2-norm of their difference ($\| U_1-U_2 \|_{S_2}$) with precision $\epsilon$, using only one clean qubit and one classical random variable. We prove a Poly$(\frac{1}{\epsilon})$ upper bound on the sample complexity, which is independent of the size of the quantum system. We then show that such a similarity metric is directly related to a functional definition of similarity of unitary operations using the conventional fidelity metric of quantum states ($F$): If $\| U_1-U_2 \|_{S_2}$ is sufficiently small (e.g. $ \leq \frac{\epsilon}{1+\sqrt{2(1/\delta - 1)}}$) then the fidelity of states obtained by processing the same randomly and uniformly picked pure state, $|\psi \rangle$, is as high as needed ($F({U}_1 |\psi \rangle, {U}_2 |\psi \rangle)\geq 1-\epsilon$) with probability exceeding $1-\delta$. We provide example applications of this efficient similarity metric estimation framework to quantum circuit learning tasks, such as finding the square root of a given unitary operation.

Ansatz-Independent Variational Quantum Classifier

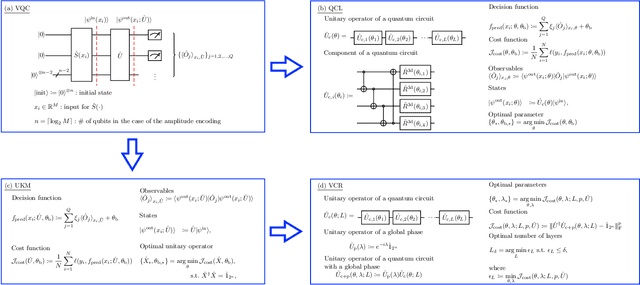
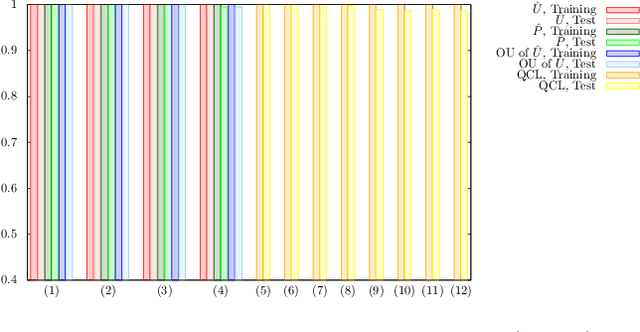
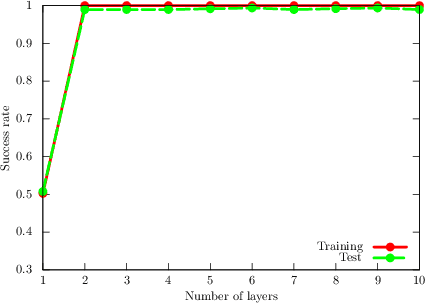
The paradigm of variational quantum classifiers (VQCs) encodes \textit{classical information} as quantum states, followed by quantum processing and then measurements to generate classical predictions. VQCs are promising candidates for efficient utilization of a near-term quantum device: classifiers involving $M$-dimensional datasets can be implemented with only $\lceil \log_2 M \rceil$ qubits by using an amplitude encoding. A general framework for designing and training VQCs, however, has not been proposed, and a fundamental understanding of its power and analytical relationships with classical classifiers are not well understood. An encouraging specific embodiment of VQCs, quantum circuit learning (QCL), utilizes an ansatz: it expresses the quantum evolution operator as a circuit with a predetermined topology and parametrized gates; training involves learning the gate parameters through optimization. In this letter, we first address the open questions about VQCs and then show that they, including QCL, fit inside the well-known kernel method. Based on such correspondence, we devise a design framework of efficient ansatz-independent VQCs, which we call the unitary kernel method (UKM): it directly optimizes the unitary evolution operator in a VQC. Thus, we show that the performance of QCL is bounded from above by the UKM. Next, we propose a variational circuit realization (VCR) for designing efficient quantum circuits for a given unitary operator. By combining the UKM with the VCR, we establish an efficient framework for constructing high-performing circuits. We finally benchmark the relatively superior performance of the UKM and the VCR via extensive numerical simulations on multiple datasets.

Quantum Expectation-Maximization Algorithm

Clustering algorithms are a cornerstone of machine learning applications. Recently, a quantum algorithm for clustering based on the k-means algorithm has been proposed by Kerenidis, Landman, Luongo and Prakash. Based on their work, we propose a quantum expectation-maximization (EM) algorithm for Gaussian mixture models (GMMs). The robustness and quantum speedup of the algorithm is demonstrated. We also show numerically the advantage of GMM over k-means for non-trivial cluster data.

A Quantum Extension of Variational Bayes Inference

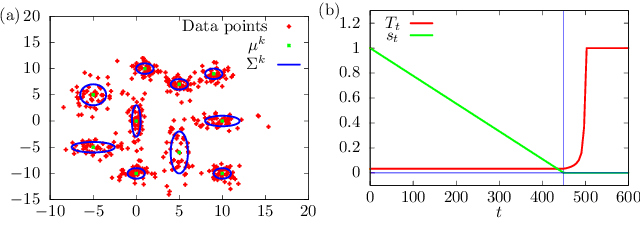
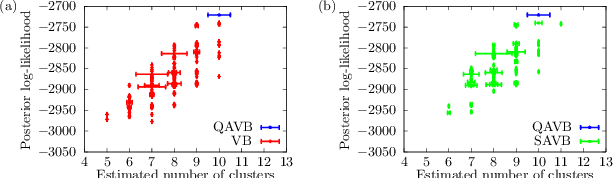
Variational Bayes (VB) inference is one of the most important algorithms in machine learning and widely used in engineering and industry. However, VB is known to suffer from the problem of local optima. In this Letter, we generalize VB by using quantum mechanics, and propose a new algorithm, which we call quantum annealing variational Bayes (QAVB) inference. We then show that QAVB drastically improve the performance of VB by applying them to a clustering problem described by a Gaussian mixture model. Finally, we discuss an intuitive understanding on how QAVB works well.

Deterministic Quantum Annealing Expectation-Maximization Algorithm

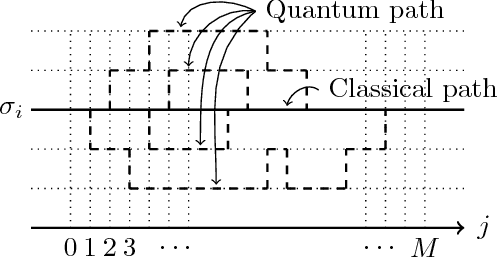
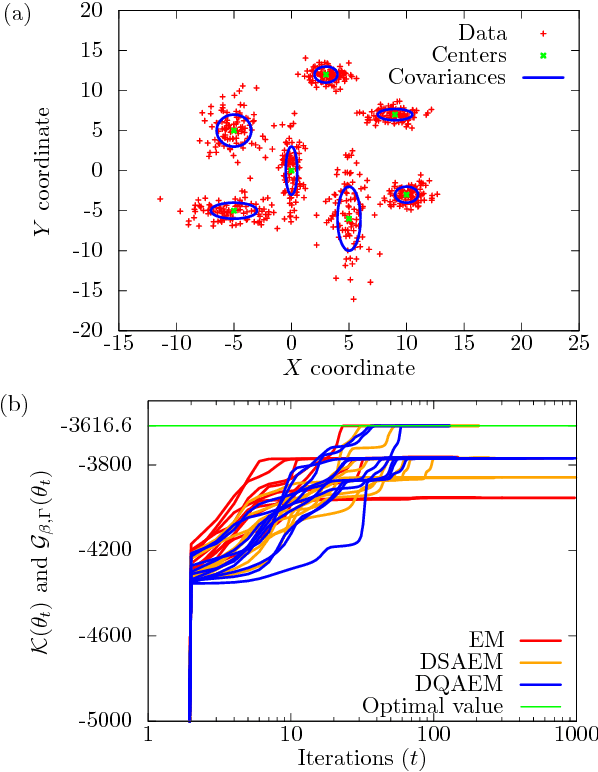
Maximum likelihood estimation (MLE) is one of the most important methods in machine learning, and the expectation-maximization (EM) algorithm is often used to obtain maximum likelihood estimates. However, EM heavily depends on initial configurations and fails to find the global optimum. On the other hand, in the field of physics, quantum annealing (QA) was proposed as a novel optimization approach. Motivated by QA, we propose a quantum annealing extension of EM, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. We also discuss its advantage in terms of the path integral formulation. Furthermore, by employing numerical simulations, we illustrate how it works in MLE and show that DQAEM outperforms EM.

Relaxation of the EM Algorithm via Quantum Annealing for Gaussian Mixture Models

We propose a modified expectation-maximization algorithm by introducing the concept of quantum annealing, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. The expectation-maximization (EM) algorithm is an established algorithm to compute maximum likelihood estimates and applied to many practical applications. However, it is known that EM heavily depends on initial values and its estimates are sometimes trapped by local optima. To solve such a problem, quantum annealing (QA) was proposed as a novel optimization approach motivated by quantum mechanics. By employing QA, we then formulate DQAEM and present a theorem that supports its stability. Finally, we demonstrate numerical simulations to confirm its efficiency.