Ansatz-Independent Variational Quantum Classifier
Paper and Code
Feb 02, 2021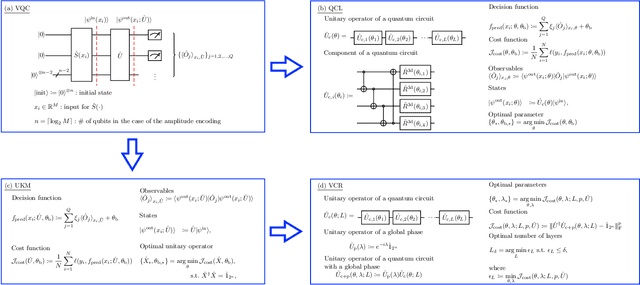
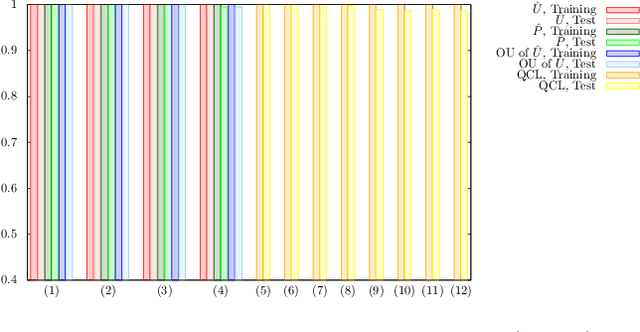
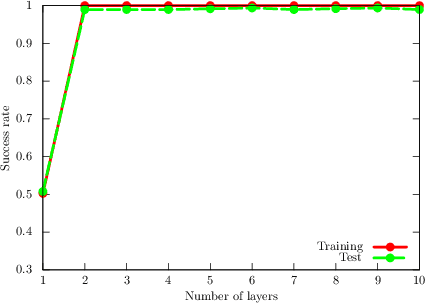
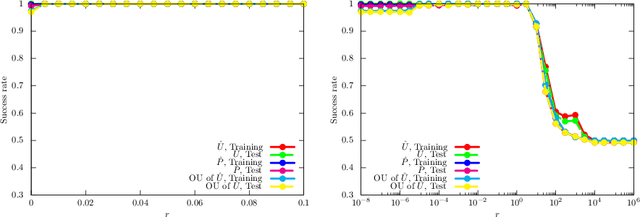
The paradigm of variational quantum classifiers (VQCs) encodes \textit{classical information} as quantum states, followed by quantum processing and then measurements to generate classical predictions. VQCs are promising candidates for efficient utilization of a near-term quantum device: classifiers involving $M$-dimensional datasets can be implemented with only $\lceil \log_2 M \rceil$ qubits by using an amplitude encoding. A general framework for designing and training VQCs, however, has not been proposed, and a fundamental understanding of its power and analytical relationships with classical classifiers are not well understood. An encouraging specific embodiment of VQCs, quantum circuit learning (QCL), utilizes an ansatz: it expresses the quantum evolution operator as a circuit with a predetermined topology and parametrized gates; training involves learning the gate parameters through optimization. In this letter, we first address the open questions about VQCs and then show that they, including QCL, fit inside the well-known kernel method. Based on such correspondence, we devise a design framework of efficient ansatz-independent VQCs, which we call the unitary kernel method (UKM): it directly optimizes the unitary evolution operator in a VQC. Thus, we show that the performance of QCL is bounded from above by the UKM. Next, we propose a variational circuit realization (VCR) for designing efficient quantum circuits for a given unitary operator. By combining the UKM with the VCR, we establish an efficient framework for constructing high-performing circuits. We finally benchmark the relatively superior performance of the UKM and the VCR via extensive numerical simulations on multiple datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge