Deterministic Quantum Annealing Expectation-Maximization Algorithm
Paper and Code
Apr 19, 2017

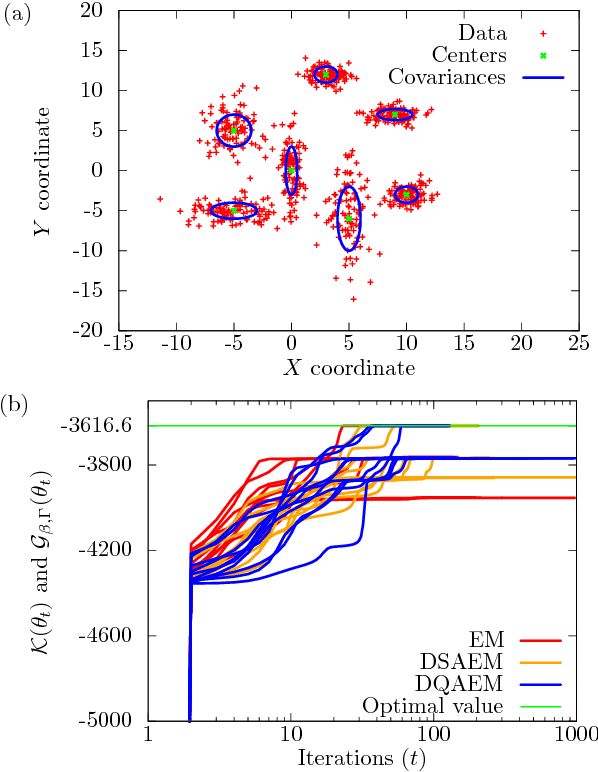
Maximum likelihood estimation (MLE) is one of the most important methods in machine learning, and the expectation-maximization (EM) algorithm is often used to obtain maximum likelihood estimates. However, EM heavily depends on initial configurations and fails to find the global optimum. On the other hand, in the field of physics, quantum annealing (QA) was proposed as a novel optimization approach. Motivated by QA, we propose a quantum annealing extension of EM, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. We also discuss its advantage in terms of the path integral formulation. Furthermore, by employing numerical simulations, we illustrate how it works in MLE and show that DQAEM outperforms EM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge