Schödinger Bridge Type Diffusion Models as an Extension of Variational Autoencoders

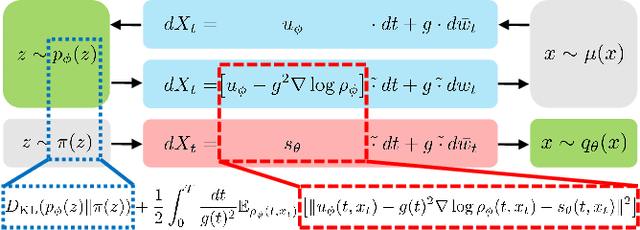
Generative diffusion models use time-forward and backward stochastic differential equations to connect the data and prior distributions. While conventional diffusion models (e.g., score-based models) only learn the backward process, more flexible frameworks have been proposed to also learn the forward process by employing the Schr\"odinger bridge (SB). However, due to the complexity of the mathematical structure behind SB-type models, we can not easily give an intuitive understanding of their objective function. In this work, we propose a unified framework to construct diffusion models by reinterpreting the SB-type models as an extension of variational autoencoders. In this context, the data processing inequality plays a crucial role. As a result, we find that the objective function consists of the prior loss and drift matching parts.

A Quantum Extension of Variational Bayes Inference

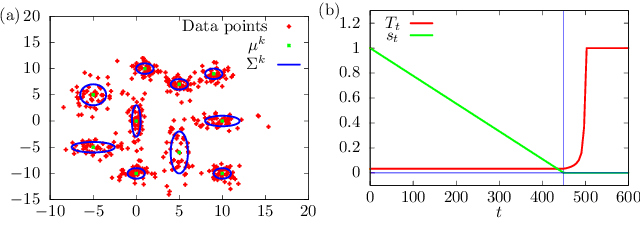
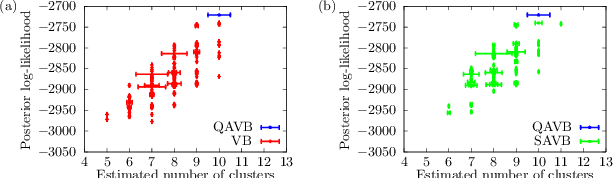
Variational Bayes (VB) inference is one of the most important algorithms in machine learning and widely used in engineering and industry. However, VB is known to suffer from the problem of local optima. In this Letter, we generalize VB by using quantum mechanics, and propose a new algorithm, which we call quantum annealing variational Bayes (QAVB) inference. We then show that QAVB drastically improve the performance of VB by applying them to a clustering problem described by a Gaussian mixture model. Finally, we discuss an intuitive understanding on how QAVB works well.

Deterministic Quantum Annealing Expectation-Maximization Algorithm

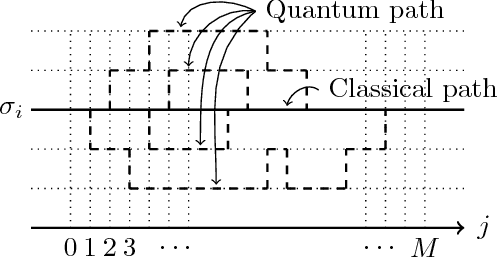
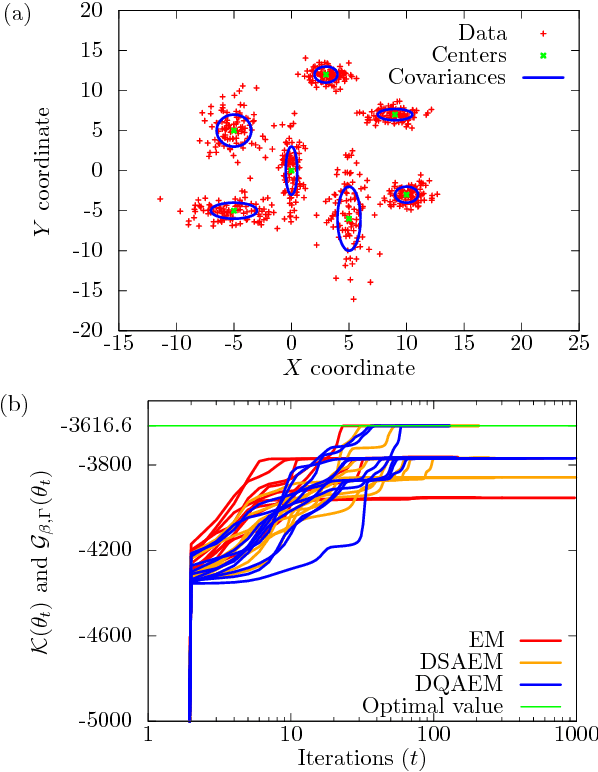
Maximum likelihood estimation (MLE) is one of the most important methods in machine learning, and the expectation-maximization (EM) algorithm is often used to obtain maximum likelihood estimates. However, EM heavily depends on initial configurations and fails to find the global optimum. On the other hand, in the field of physics, quantum annealing (QA) was proposed as a novel optimization approach. Motivated by QA, we propose a quantum annealing extension of EM, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. We also discuss its advantage in terms of the path integral formulation. Furthermore, by employing numerical simulations, we illustrate how it works in MLE and show that DQAEM outperforms EM.

Relaxation of the EM Algorithm via Quantum Annealing for Gaussian Mixture Models

We propose a modified expectation-maximization algorithm by introducing the concept of quantum annealing, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. The expectation-maximization (EM) algorithm is an established algorithm to compute maximum likelihood estimates and applied to many practical applications. However, it is known that EM heavily depends on initial values and its estimates are sometimes trapped by local optima. To solve such a problem, quantum annealing (QA) was proposed as a novel optimization approach motivated by quantum mechanics. By employing QA, we then formulate DQAEM and present a theorem that supports its stability. Finally, we demonstrate numerical simulations to confirm its efficiency.