Simulation-free and finite-time diffusion model

The performance of generative diffusion models is determined by the choice of the reference diffusion process connecting the empirical and prior distributions. Conventional approaches typically trade off simulation-free training against finite-time generation. We propose a framework for designing the reference process that achieves both simultaneously. The key idea is to prescribe tractable time-dependent conditional distributions and then construct the reference process realizing them as its marginals. This framework reveals that score matching is not fundamental to diffusion-model training but instead emerges naturally through reversal of the reference process. We further show that conditional flow matching arises as the small-noise limit of the proposed framework.

Schödinger Bridge Type Diffusion Models as an Extension of Variational Autoencoders

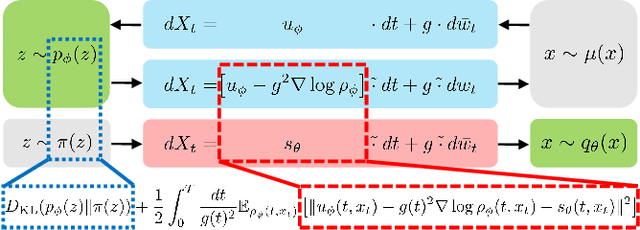
Generative diffusion models use time-forward and backward stochastic differential equations to connect the data and prior distributions. While conventional diffusion models (e.g., score-based models) only learn the backward process, more flexible frameworks have been proposed to also learn the forward process by employing the Schr\"odinger bridge (SB). However, due to the complexity of the mathematical structure behind SB-type models, we can not easily give an intuitive understanding of their objective function. In this work, we propose a unified framework to construct diffusion models by reinterpreting the SB-type models as an extension of variational autoencoders. In this context, the data processing inequality plays a crucial role. As a result, we find that the objective function consists of the prior loss and drift matching parts.