Deterministic Quantum Annealing Expectation-Maximization Algorithm

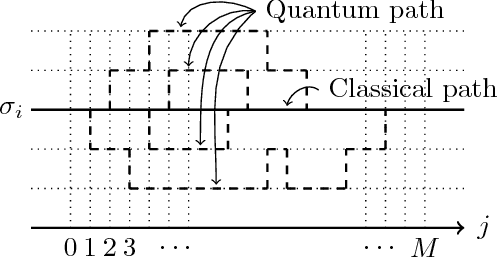
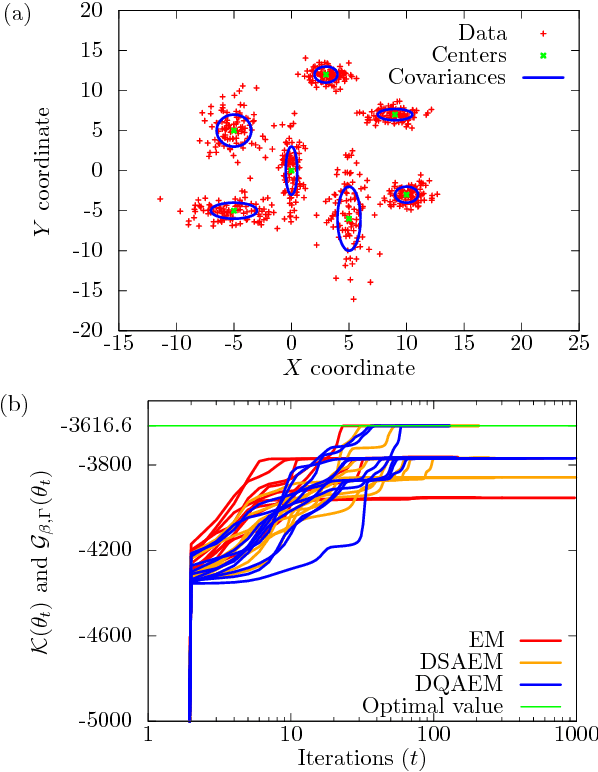
Maximum likelihood estimation (MLE) is one of the most important methods in machine learning, and the expectation-maximization (EM) algorithm is often used to obtain maximum likelihood estimates. However, EM heavily depends on initial configurations and fails to find the global optimum. On the other hand, in the field of physics, quantum annealing (QA) was proposed as a novel optimization approach. Motivated by QA, we propose a quantum annealing extension of EM, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. We also discuss its advantage in terms of the path integral formulation. Furthermore, by employing numerical simulations, we illustrate how it works in MLE and show that DQAEM outperforms EM.

Relaxation of the EM Algorithm via Quantum Annealing for Gaussian Mixture Models

We propose a modified expectation-maximization algorithm by introducing the concept of quantum annealing, which we call the deterministic quantum annealing expectation-maximization (DQAEM) algorithm. The expectation-maximization (EM) algorithm is an established algorithm to compute maximum likelihood estimates and applied to many practical applications. However, it is known that EM heavily depends on initial values and its estimates are sometimes trapped by local optima. To solve such a problem, quantum annealing (QA) was proposed as a novel optimization approach motivated by quantum mechanics. By employing QA, we then formulate DQAEM and present a theorem that supports its stability. Finally, we demonstrate numerical simulations to confirm its efficiency.

Relaxation of the EM Algorithm via Quantum Annealing

The EM algorithm is a novel numerical method to obtain maximum likelihood estimates and is often used for practical calculations. However, many of maximum likelihood estimation problems are nonconvex, and it is known that the EM algorithm fails to give the optimal estimate by being trapped by local optima. In order to deal with this difficulty, we propose a deterministic quantum annealing EM algorithm by introducing the mathematical mechanism of quantum fluctuations into the conventional EM algorithm because quantum fluctuations induce the tunnel effect and are expected to relax the difficulty of nonconvex optimization problems in the maximum likelihood estimation problems. We show a theorem that guarantees its convergence and give numerical experiments to verify its efficiency.