Enhancing Vector Quantization with Distributional Matching: A Theoretical and Empirical Study

The success of autoregressive models largely depends on the effectiveness of vector quantization, a technique that discretizes continuous features by mapping them to the nearest code vectors within a learnable codebook. Two critical issues in existing vector quantization methods are training instability and codebook collapse. Training instability arises from the gradient discrepancy introduced by the straight-through estimator, especially in the presence of significant quantization errors, while codebook collapse occurs when only a small subset of code vectors are utilized during training. A closer examination of these issues reveals that they are primarily driven by a mismatch between the distributions of the features and code vectors, leading to unrepresentative code vectors and significant data information loss during compression. To address this, we employ the Wasserstein distance to align these two distributions, achieving near 100\% codebook utilization and significantly reducing the quantization error. Both empirical and theoretical analyses validate the effectiveness of the proposed approach.

Estimation of Ridge Using Nonlinear Transformation on Density Function

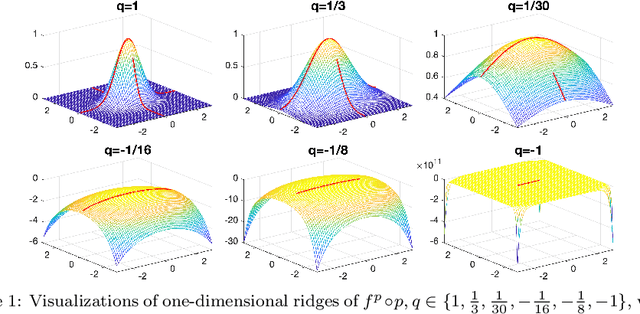
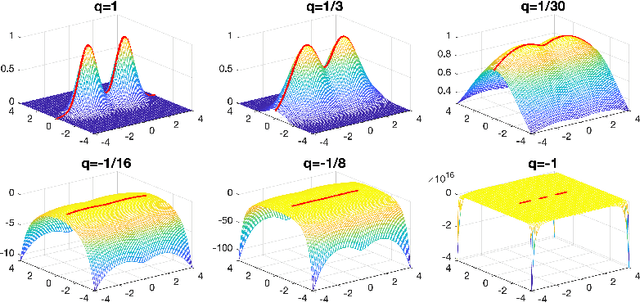
Ridges play a vital role in accurately approximating the underlying structure of manifolds. In this paper, we explore the ridge's variation by applying a concave nonlinear transformation to the density function. Through the derivation of the Hessian matrix, we observe that nonlinear transformations yield a rank-one modification of the Hessian matrix. Leveraging the variational properties of eigenvalue problems, we establish a partial order inclusion relationship among the corresponding ridges. We intuitively discover that the transformation can lead to improved estimation of the tangent space via rank-one modification of the Hessian matrix. To validate our theories, we conduct extensive numerical experiments on synthetic and real-world datasets that demonstrate the superiority of the ridges obtained from our transformed approach in approximating the underlying truth manifold compared to other manifold fitting algorithms.

Fast global convergence of gradient descent for low-rank matrix approximation

This paper investigates gradient descent for solving low-rank matrix approximation problems. We begin by establishing the local linear convergence of gradient descent for symmetric matrix approximation. Building on this result, we prove the rapid global convergence of gradient descent, particularly when initialized with small random values. Remarkably, we show that even with moderate random initialization, which includes small random initialization as a special case, gradient descent achieves fast global convergence in scenarios where the top eigenvalues are identical. Furthermore, we extend our analysis to address asymmetric matrix approximation problems and investigate the effectiveness of a retraction-free eigenspace computation method. Numerical experiments strongly support our theory. In particular, the retraction-free algorithm outperforms the corresponding Riemannian gradient descent method, resulting in a significant 29\% reduction in runtime.

Bounded Projection Matrix Approximation with Applications to Community Detection

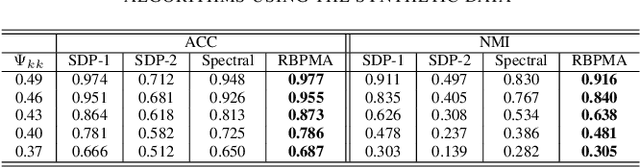
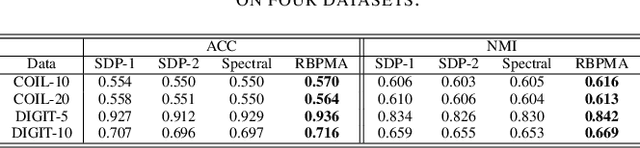
Community detection is an important problem in unsupervised learning. This paper proposes to solve a projection matrix approximation problem with an additional entrywise bounded constraint. Algorithmically, we introduce a new differentiable convex penalty and derive an alternating direction method of multipliers (ADMM) algorithm. Theoretically, we establish the convergence properties of the proposed algorithm. Numerical experiments demonstrate the superiority of our algorithm over its competitors, such as the semi-definite relaxation method and spectral clustering.

Statistical Analysis of Karcher Means for Random Restricted PSD Matrices

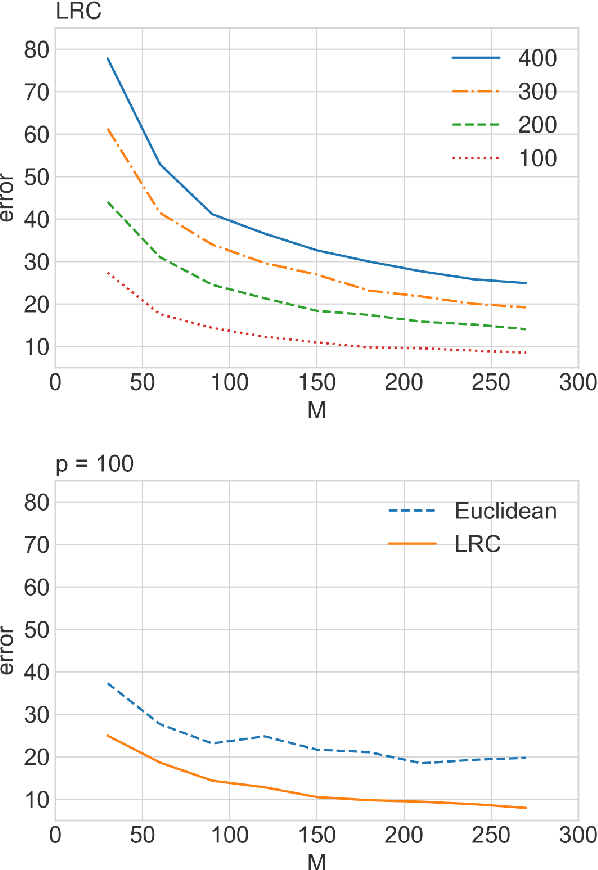
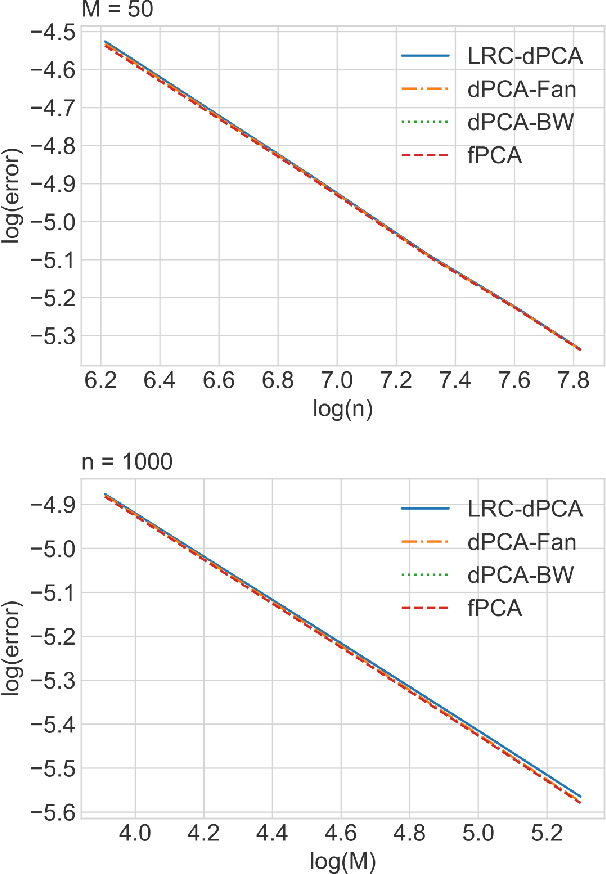
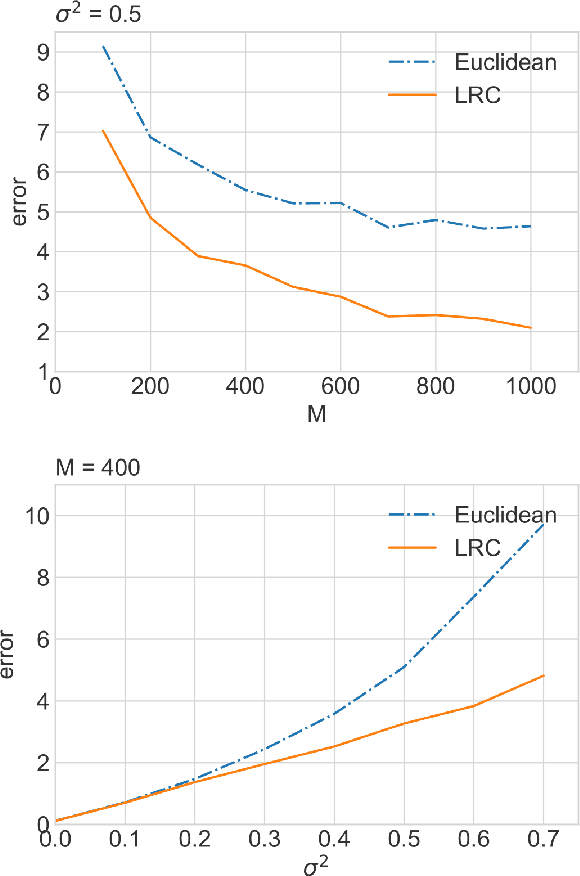
Non-asymptotic statistical analysis is often missing for modern geometry-aware machine learning algorithms due to the possibly intricate non-linear manifold structure. This paper studies an intrinsic mean model on the manifold of restricted positive semi-definite matrices and provides a non-asymptotic statistical analysis of the Karcher mean. We also consider a general extrinsic signal-plus-noise model, under which a deterministic error bound of the Karcher mean is provided. As an application, we show that the distributed principal component analysis algorithm, LRC-dPCA, achieves the same performance as the full sample PCA algorithm. Numerical experiments lend strong support to our theories.

Quadratic Matrix Factorization with Applications to Manifold Learning

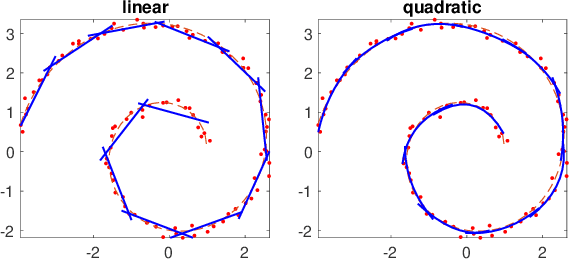
Matrix factorization is a popular framework for modeling low-rank data matrices. Motivated by manifold learning problems, this paper proposes a quadratic matrix factorization (QMF) framework to learn the curved manifold on which the dataset lies. Unlike local linear methods such as the local principal component analysis, QMF can better exploit the curved structure of the underlying manifold. Algorithmically, we propose an alternating minimization algorithm to optimize QMF and establish its theoretical convergence properties. Moreover, to avoid possible over-fitting, we then propose a regularized QMF algorithm and discuss how to tune its regularization parameter. Finally, we elaborate how to apply the regularized QMF to manifold learning problems. Experiments on a synthetic manifold learning dataset and two real datasets, including the MNIST handwritten dataset and a cryogenic electron microscopy dataset, demonstrate the superiority of the proposed method over its competitors.

Distributed Sparse Multicategory Discriminant Analysis

This paper proposes a convex formulation for sparse multicategory linear discriminant analysis and then extend it to the distributed setting when data are stored across multiple sites. The key observation is that for the purpose of classification it suffices to recover the discriminant subspace which is invariant to orthogonal transformations. Theoretically, we establish statistical properties ensuring that the distributed sparse multicategory linear discriminant analysis performs as good as the centralized version after {a few rounds} of communications. Numerical studies lend strong support to our methodology and theory.