Subspace-Constrained Quadratic Matrix Factorization: Algorithm and Applications

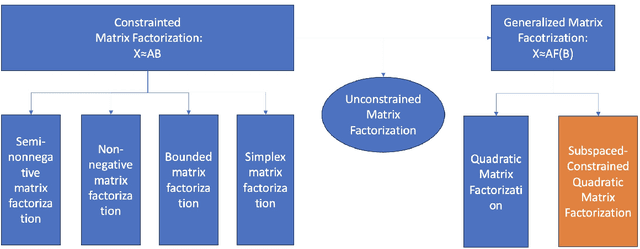
Matrix Factorization has emerged as a widely adopted framework for modeling data exhibiting low-rank structures. To address challenges in manifold learning, this paper presents a subspace-constrained quadratic matrix factorization model. The model is designed to jointly learn key low-dimensional structures, including the tangent space, the normal subspace, and the quadratic form that links the tangent space to a low-dimensional representation. We solve the proposed factorization model using an alternating minimization method, involving an in-depth investigation of nonlinear regression and projection subproblems. Theoretical properties of the quadratic projection problem and convergence characteristics of the alternating strategy are also investigated. To validate our approach, we conduct numerical experiments on synthetic and real-world datasets. Results demonstrate that our model outperforms existing methods, highlighting its robustness and efficacy in capturing core low-dimensional structures.

Regularized Projection Matrix Approximation with Applications to Community Detection

This paper introduces a regularized projection matrix approximation framework aimed at recovering cluster information from the affinity matrix. The model is formulated as a projection approximation problem incorporating an entrywise penalty function. We explore three distinct penalty functions addressing bounded, positive, and sparse scenarios, respectively, and derive the Alternating Direction Method of Multipliers (ADMM) algorithm to solve the problem. Then, we provide a theoretical analysis establishing the convergence properties of the proposed algorithm. Extensive numerical experiments on both synthetic and real-world datasets demonstrate that our regularized projection matrix approximation approach significantly outperforms state-of-the-art methods in terms of clustering performance.

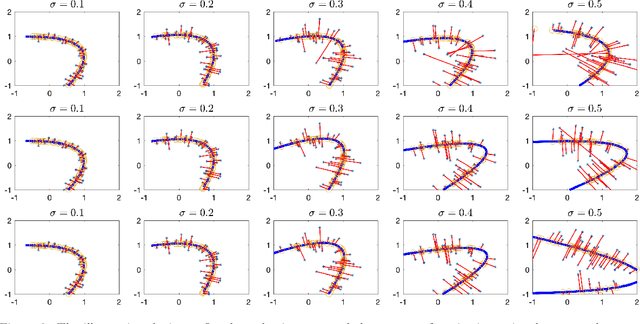
Estimation of Ridge Using Nonlinear Transformation on Density Function

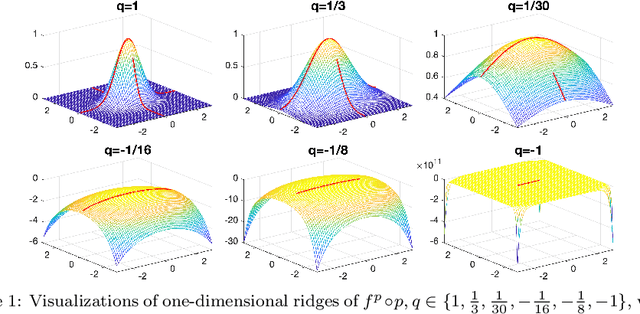
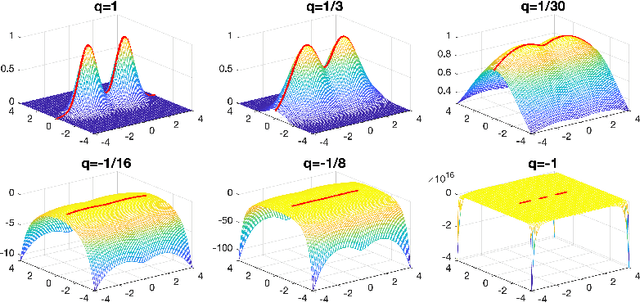
Ridges play a vital role in accurately approximating the underlying structure of manifolds. In this paper, we explore the ridge's variation by applying a concave nonlinear transformation to the density function. Through the derivation of the Hessian matrix, we observe that nonlinear transformations yield a rank-one modification of the Hessian matrix. Leveraging the variational properties of eigenvalue problems, we establish a partial order inclusion relationship among the corresponding ridges. We intuitively discover that the transformation can lead to improved estimation of the tangent space via rank-one modification of the Hessian matrix. To validate our theories, we conduct extensive numerical experiments on synthetic and real-world datasets that demonstrate the superiority of the ridges obtained from our transformed approach in approximating the underlying truth manifold compared to other manifold fitting algorithms.

Bounded Projection Matrix Approximation with Applications to Community Detection

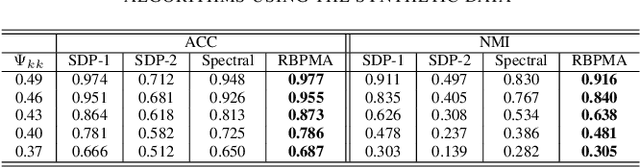
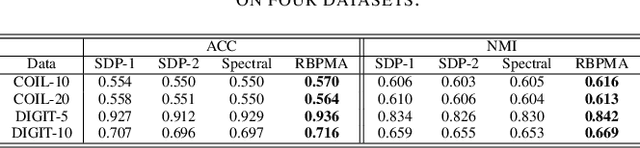
Community detection is an important problem in unsupervised learning. This paper proposes to solve a projection matrix approximation problem with an additional entrywise bounded constraint. Algorithmically, we introduce a new differentiable convex penalty and derive an alternating direction method of multipliers (ADMM) algorithm. Theoretically, we establish the convergence properties of the proposed algorithm. Numerical experiments demonstrate the superiority of our algorithm over its competitors, such as the semi-definite relaxation method and spectral clustering.

Quadratic Matrix Factorization with Applications to Manifold Learning

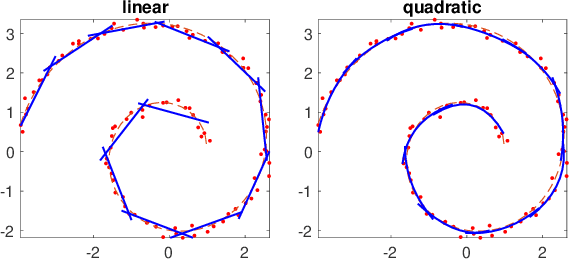
Matrix factorization is a popular framework for modeling low-rank data matrices. Motivated by manifold learning problems, this paper proposes a quadratic matrix factorization (QMF) framework to learn the curved manifold on which the dataset lies. Unlike local linear methods such as the local principal component analysis, QMF can better exploit the curved structure of the underlying manifold. Algorithmically, we propose an alternating minimization algorithm to optimize QMF and establish its theoretical convergence properties. Moreover, to avoid possible over-fitting, we then propose a regularized QMF algorithm and discuss how to tune its regularization parameter. Finally, we elaborate how to apply the regularized QMF to manifold learning problems. Experiments on a synthetic manifold learning dataset and two real datasets, including the MNIST handwritten dataset and a cryogenic electron microscopy dataset, demonstrate the superiority of the proposed method over its competitors.