Zhigang Yao
Enhanced High-Dimensional Data Visualization through Adaptive Multi-Scale Manifold Embedding
Mar 19, 2025Abstract:To address the dual challenges of the curse of dimensionality and the difficulty in separating intra-cluster and inter-cluster structures in high-dimensional manifold embedding, we proposes an Adaptive Multi-Scale Manifold Embedding (AMSME) algorithm. By introducing ordinal distance to replace traditional Euclidean distances, we theoretically demonstrate that ordinal distance overcomes the constraints of the curse of dimensionality in high-dimensional spaces, effectively distinguishing heterogeneous samples. We design an adaptive neighborhood adjustment method to construct similarity graphs that simultaneously balance intra-cluster compactness and inter-cluster separability. Furthermore, we develop a two-stage embedding framework: the first stage achieves preliminary cluster separation while preserving connectivity between structurally similar clusters via the similarity graph, and the second stage enhances inter-cluster separation through a label-driven distance reweighting. Experimental results demonstrate that AMSME significantly preserves intra-cluster topological structures and improves inter-cluster separation on real-world datasets. Additionally, leveraging its multi-resolution analysis capability, AMSME discovers novel neuronal subtypes in the mouse lumbar dorsal root ganglion scRNA-seq dataset, with marker gene analysis revealing their distinct biological roles.
Estimation of Ridge Using Nonlinear Transformation on Density Function
Jun 09, 2023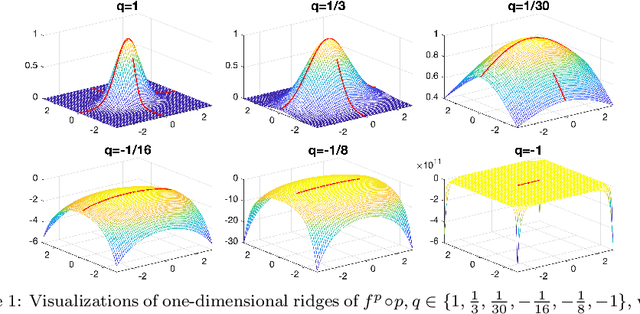

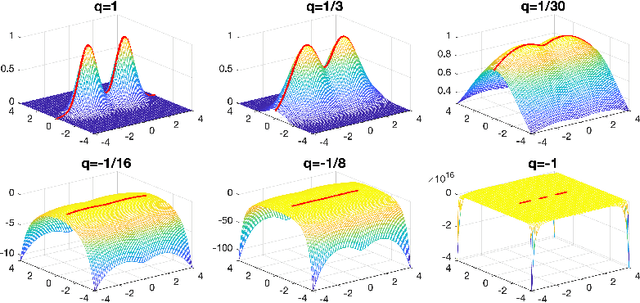

Abstract:Ridges play a vital role in accurately approximating the underlying structure of manifolds. In this paper, we explore the ridge's variation by applying a concave nonlinear transformation to the density function. Through the derivation of the Hessian matrix, we observe that nonlinear transformations yield a rank-one modification of the Hessian matrix. Leveraging the variational properties of eigenvalue problems, we establish a partial order inclusion relationship among the corresponding ridges. We intuitively discover that the transformation can lead to improved estimation of the tangent space via rank-one modification of the Hessian matrix. To validate our theories, we conduct extensive numerical experiments on synthetic and real-world datasets that demonstrate the superiority of the ridges obtained from our transformed approach in approximating the underlying truth manifold compared to other manifold fitting algorithms.
Manifold Fitting in Ambient Space
Sep 30, 2019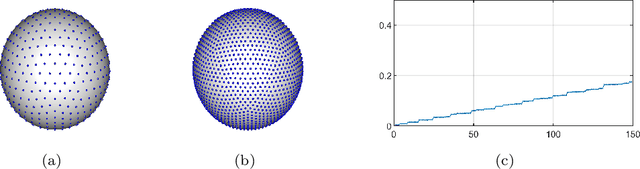
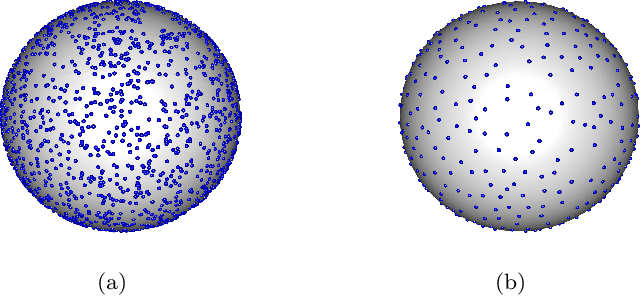
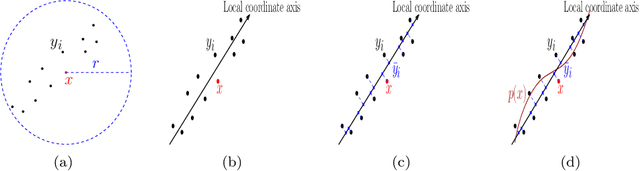
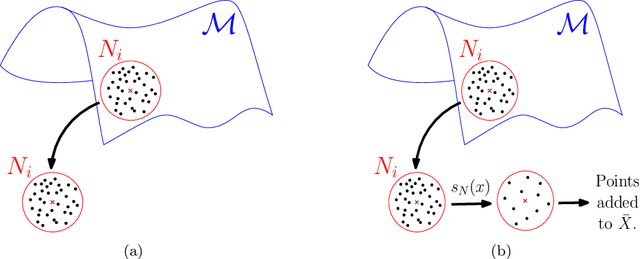
Abstract:Modern data sets in many applications no longer comprise samples of real vectors in a real vector space but samples of much more complex structures which may be represented as points in a space with certain underlying geometric structure, namely a manifold. Manifold learning is an emerging field for learning the underlying structure. The study of manifold learning can be split into two main branches, namely dimension reduction and manifold fitting. With the aim of interacting statistics and geometry, we tackle the problem of manifold fitting in the ambient space. Inspired by the relation between the eigenvalues of the Laplace-Beltrami operator and the geometry of a manifold, we aim to find a small set of points that preserve the geometry of the underlying manifold. Based on this relationship, we extend the idea of subsampling to noisy datasets in high dimensional space and utilize the Moving Least Squares (MLS) approach to approximate the underlying manifold. We analyze the two core steps in our proposed method theoretically and also provide the bounds for the MLS approach. Our simulation results and real data analysis demonstrate the superiority of our method in estimating the underlying manifold from noisy data.
Manifold Fitting under Unbounded Noise
Sep 23, 2019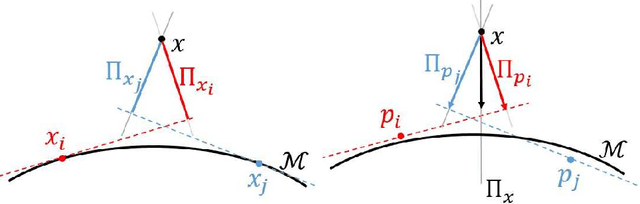
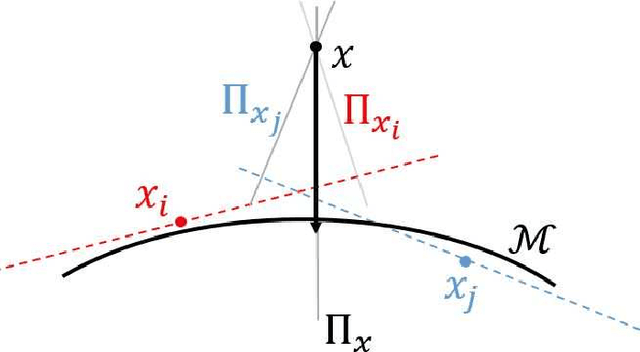
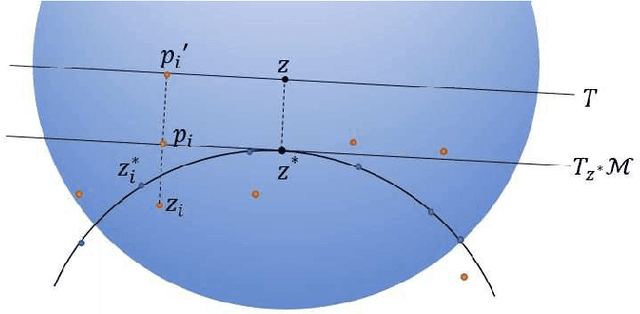

Abstract:There has been an emerging trend in non-Euclidean dimension reduction of aiming to recover a low dimensional structure, namely a manifold, underlying the high dimensional data. Recovering the manifold requires the noise to be of certain concentration. Existing methods address this problem by constructing an output manifold based on the tangent space estimation at each sample point. Although theoretical convergence for these methods is guaranteed, either the samples are noiseless or the noise is bounded. However, if the noise is unbounded, which is a common scenario, the tangent space estimation of the noisy samples will be blurred, thereby breaking the manifold fitting. In this paper, we introduce a new manifold-fitting method, by which the output manifold is constructed by directly estimating the tangent spaces at the projected points on the underlying manifold, rather than at the sample points, to decrease the error caused by the noise. Our new method provides theoretical convergence, in terms of the upper bound on the Hausdorff distance between the output and underlying manifold and the lower bound on the reach of the output manifold, when the noise is unbounded. Numerical simulations are provided to validate our theoretical findings and demonstrate the advantages of our method over other relevant methods. Finally, our method is applied to real data examples.
Principal Boundary on Riemannian Manifolds
Oct 21, 2017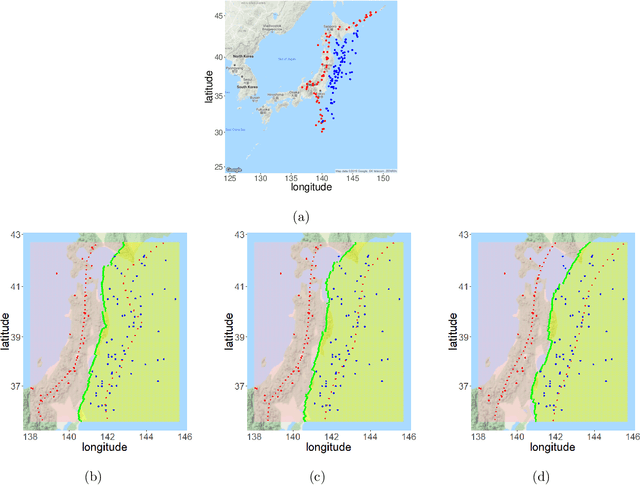


Abstract:We revisit the classification problem and focus on nonlinear methods for classification on manifolds. For multivariate datasets lying on an embedded nonlinear Riemannian manifold within the higher-dimensional space, our aim is to acquire a classification boundary between the classes with labels. Motivated by the principal flow [Panaretos, Pham and Yao, 2014], a curve that moves along a path of the maximum variation of the data, we introduce the principal boundary. From the classification perspective, the principal boundary is defined as an optimal curve that moves in between the principal flows traced out from two classes of the data, and at any point on the boundary, it maximizes the margin between the two classes. We estimate the boundary in quality with its direction supervised by the two principal flows. We show that the principal boundary yields the usual decision boundary found by the support vector machine, in the sense that locally, the two boundaries coincide. By means of examples, we illustrate how to find, use and interpret the principal boundary.
Optimal classification in sparse Gaussian graphic model
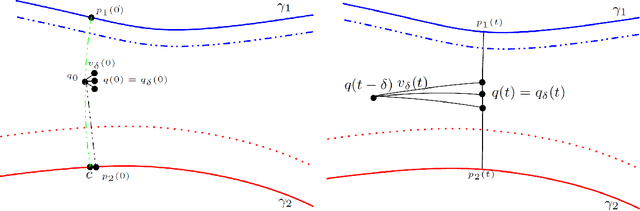
Nov 20, 2013
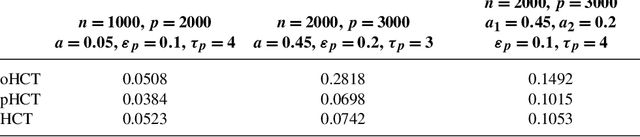

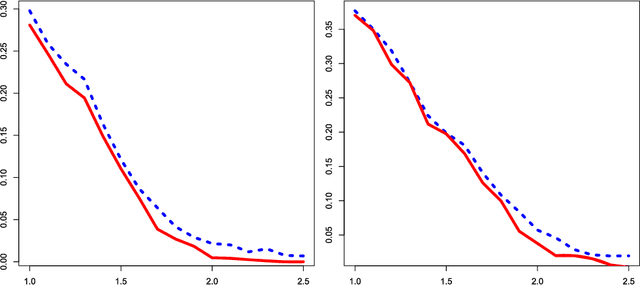
Abstract:Consider a two-class classification problem where the number of features is much larger than the sample size. The features are masked by Gaussian noise with mean zero and covariance matrix $\Sigma$, where the precision matrix $\Omega=\Sigma^{-1}$ is unknown but is presumably sparse. The useful features, also unknown, are sparse and each contributes weakly (i.e., rare and weak) to the classification decision. By obtaining a reasonably good estimate of $\Omega$, we formulate the setting as a linear regression model. We propose a two-stage classification method where we first select features by the method of Innovated Thresholding (IT), and then use the retained features and Fisher's LDA for classification. In this approach, a crucial problem is how to set the threshold of IT. We approach this problem by adapting the recent innovation of Higher Criticism Thresholding (HCT). We find that when useful features are rare and weak, the limiting behavior of HCT is essentially just as good as the limiting behavior of ideal threshold, the threshold one would choose if the underlying distribution of the signals is known (if only). Somewhat surprisingly, when $\Omega$ is sufficiently sparse, its off-diagonal coordinates usually do not have a major influence over the classification decision. Compared to recent work in the case where $\Omega$ is the identity matrix [Proc. Natl. Acad. Sci. USA 105 (2008) 14790-14795; Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 367 (2009) 4449-4470], the current setting is much more general, which needs a new approach and much more sophisticated analysis. One key component of the analysis is the intimate relationship between HCT and Fisher's separation. Another key component is the tight large-deviation bounds for empirical processes for data with unconventional correlation structures, where graph theory on vertex coloring plays an important role.
* Published in at http://dx.doi.org/10.1214/13-AOS1163 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge