Manifold Fitting in Ambient Space
Paper and Code
Sep 30, 2019
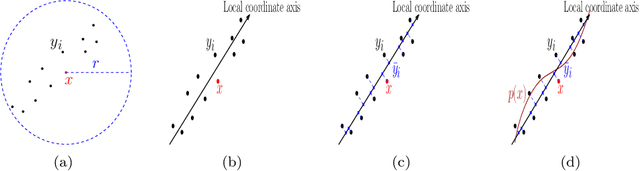
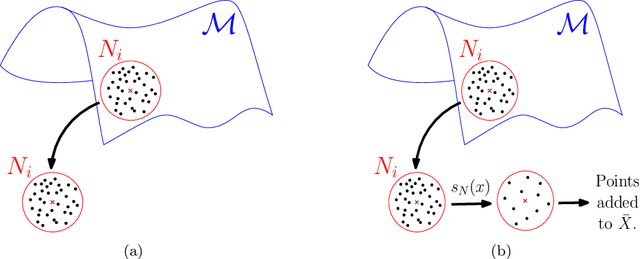
Modern data sets in many applications no longer comprise samples of real vectors in a real vector space but samples of much more complex structures which may be represented as points in a space with certain underlying geometric structure, namely a manifold. Manifold learning is an emerging field for learning the underlying structure. The study of manifold learning can be split into two main branches, namely dimension reduction and manifold fitting. With the aim of interacting statistics and geometry, we tackle the problem of manifold fitting in the ambient space. Inspired by the relation between the eigenvalues of the Laplace-Beltrami operator and the geometry of a manifold, we aim to find a small set of points that preserve the geometry of the underlying manifold. Based on this relationship, we extend the idea of subsampling to noisy datasets in high dimensional space and utilize the Moving Least Squares (MLS) approach to approximate the underlying manifold. We analyze the two core steps in our proposed method theoretically and also provide the bounds for the MLS approach. Our simulation results and real data analysis demonstrate the superiority of our method in estimating the underlying manifold from noisy data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge