Manifold Fitting under Unbounded Noise

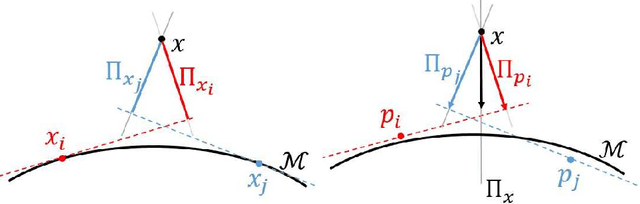
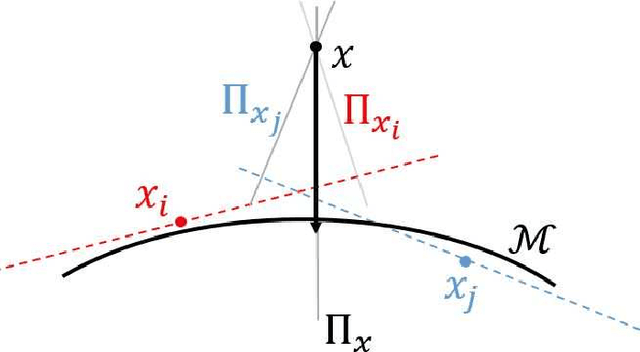
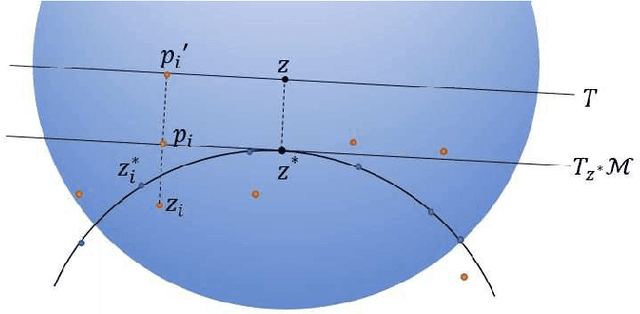
There has been an emerging trend in non-Euclidean dimension reduction of aiming to recover a low dimensional structure, namely a manifold, underlying the high dimensional data. Recovering the manifold requires the noise to be of certain concentration. Existing methods address this problem by constructing an output manifold based on the tangent space estimation at each sample point. Although theoretical convergence for these methods is guaranteed, either the samples are noiseless or the noise is bounded. However, if the noise is unbounded, which is a common scenario, the tangent space estimation of the noisy samples will be blurred, thereby breaking the manifold fitting. In this paper, we introduce a new manifold-fitting method, by which the output manifold is constructed by directly estimating the tangent spaces at the projected points on the underlying manifold, rather than at the sample points, to decrease the error caused by the noise. Our new method provides theoretical convergence, in terms of the upper bound on the Hausdorff distance between the output and underlying manifold and the lower bound on the reach of the output manifold, when the noise is unbounded. Numerical simulations are provided to validate our theoretical findings and demonstrate the advantages of our method over other relevant methods. Finally, our method is applied to real data examples.