Robust Weight Initialization for Tanh Neural Networks with Fixed Point Analysis

As a neural network's depth increases, it can achieve strong generalization performance. Training, however, becomes challenging due to gradient issues. Theoretical research and various methods have been introduced to address this issues. However, research on weight initialization methods that can be effectively applied to tanh neural networks of varying sizes still needs to be completed. This paper presents a novel weight initialization method for Feedforward Neural Networks with tanh activation function. Based on an analysis of the fixed points of the function $\tanh(ax)$, our proposed method aims to determine values of $a$ that prevent the saturation of activations. A series of experiments on various classification datasets demonstrate that the proposed method is more robust to network size variations than the existing method. Furthermore, when applied to Physics-Informed Neural Networks, the method exhibits faster convergence and robustness to variations of the network size compared to Xavier initialization in problems of Partial Differential Equations.

Improved identification of breakpoints in piecewise regression and its applications

Identifying breakpoints in piecewise regression is critical in enhancing the reliability and interpretability of data fitting. In this paper, we propose novel algorithms based on the greedy algorithm to accurately and efficiently identify breakpoints in piecewise polynomial regression. The algorithm updates the breakpoints to minimize the error by exploring the neighborhood of each breakpoint. It has a fast convergence rate and stability to find optimal breakpoints. Moreover, it can determine the optimal number of breakpoints. The computational results for real and synthetic data show that its accuracy is better than any existing methods. The real-world datasets demonstrate that breakpoints through the proposed algorithm provide valuable data information.

Improved weight initialization for deep and narrow feedforward neural network

Appropriate weight initialization settings, along with the ReLU activation function, have been a cornerstone of modern deep learning, making it possible to train and deploy highly effective and efficient neural network models across diverse artificial intelligence. The problem of dying ReLU, where ReLU neurons become inactive and yield zero output, presents a significant challenge in the training of deep neural networks with ReLU activation function. Theoretical research and various methods have been introduced to address the problem. However, even with these methods and research, training remains challenging for extremely deep and narrow feedforward networks with ReLU activation function. In this paper, we propose a new weight initialization method to address this issue. We prove the properties of the proposed initial weight matrix and demonstrate how these properties facilitate the effective propagation of signal vectors. Through a series of experiments and comparisons with existing methods, we demonstrate the effectiveness of the new initialization method.

Algorithm Unrolling for Massive Access via Deep Neural Network with Theoretical Guarantee

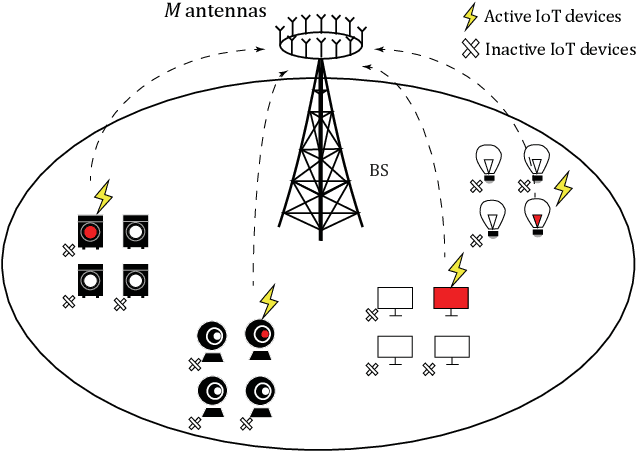
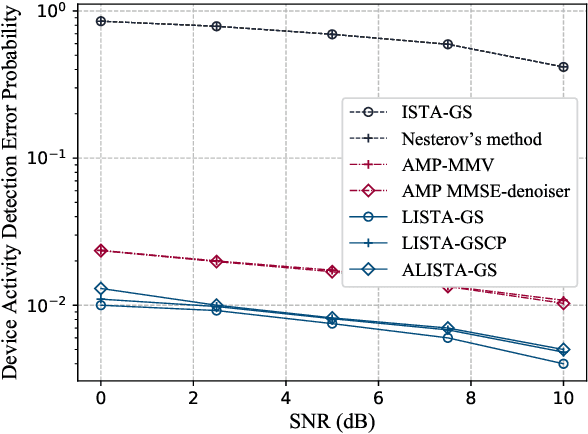
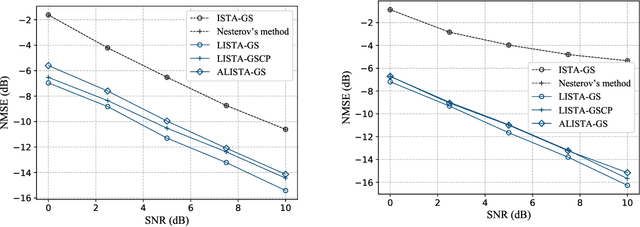
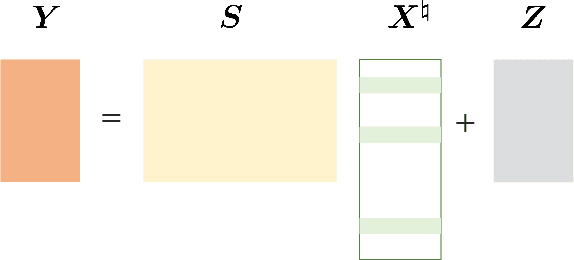
Massive access is a critical design challenge of Internet of Things (IoT) networks. In this paper, we consider the grant-free uplink transmission of an IoT network with a multiple-antenna base station (BS) and a large number of single-antenna IoT devices. Taking into account the sporadic nature of IoT devices, we formulate the joint activity detection and channel estimation (JADCE) problem as a group-sparse matrix estimation problem. This problem can be solved by applying the existing compressed sensing techniques, which however either suffer from high computational complexities or lack of algorithm robustness. To this end, we propose a novel algorithm unrolling framework based on the deep neural network to simultaneously achieve low computational complexity and high robustness for solving the JADCE problem. Specifically, we map the original iterative shrinkage thresholding algorithm (ISTA) into an unrolled recurrent neural network (RNN), thereby improving the convergence rate and computational efficiency through end-to-end training. Moreover, the proposed algorithm unrolling approach inherits the structure and domain knowledge of the ISTA, thereby maintaining the algorithm robustness, which can handle non-Gaussian preamble sequence matrix in massive access. With rigorous theoretical analysis, we further simplify the unrolled network structure by reducing the redundant training parameters. Furthermore, we prove that the simplified unrolled deep neural network structures enjoy a linear convergence rate. Extensive simulations based on various preamble signatures show that the proposed unrolled networks outperform the existing methods in terms of the convergence rate, robustness and estimation accuracy.

An Algebraic-Geometric Approach to Shuffled Linear Regression

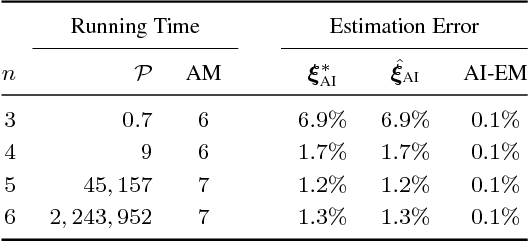
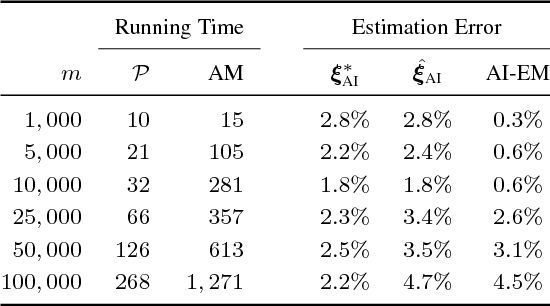
Shuffled linear regression is the problem of performing a linear regression fit to a dataset for which the correspondences between the independent samples and the observations are unknown. Such a problem arises in diverse domains such as computer vision, communications and biology. In its simplest form, it is tantamount to solving a linear system of equations, for which the entries of the right hand side vector have been permuted. This type of data corruption renders the linear regression task considerably harder, even in the absence of other corruptions, such as noise, outliers or missing entries. Existing methods are either applicable only to noiseless data or they are very sensitive to initialization and work only for partially shuffled data. In this paper we address both of these issues via an algebraic geometric approach, which uses symmetric polynomials to extract permutation-invariant constraints that the parameters $\boldsymbol{x} \in \mathbb{R}^n$ of the linear regression model must satisfy. This naturally leads to a polynomial system of $n$ equations in $n$ unknowns, which contains $\boldsymbol{x}$ in its root locus. Using the machinery of algebraic geometry we prove that as long as the independent samples are generic, this polynomial system is always consistent with at most $n!$ complex roots, regardless of any type of corruption inflicted on the observations. The algorithmic implication of this fact is that one can always solve this polynomial system and use its most suitable root as initialization to the Expectation Maximization algorithm. To the best of our knowledge, the resulting method is the first working solution for small values of $n$ able to handle thousands of fully shuffled noisy observations in milliseconds.