A domain decomposition-based autoregressive deep learning model for unsteady and nonlinear partial differential equations

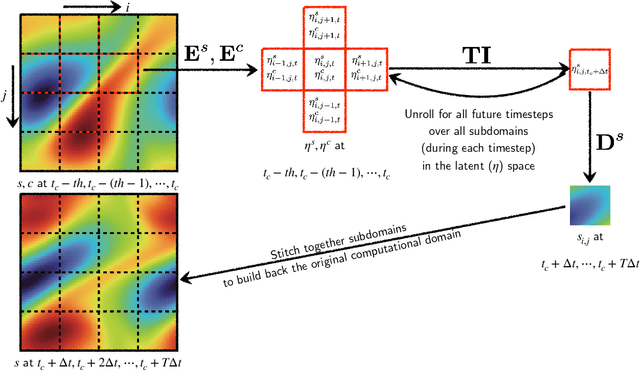
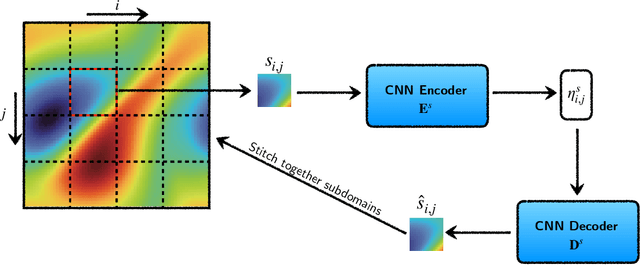
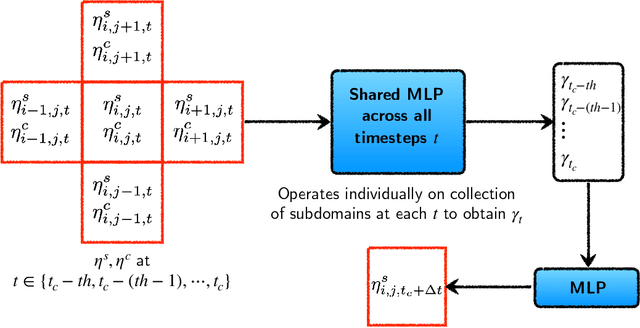
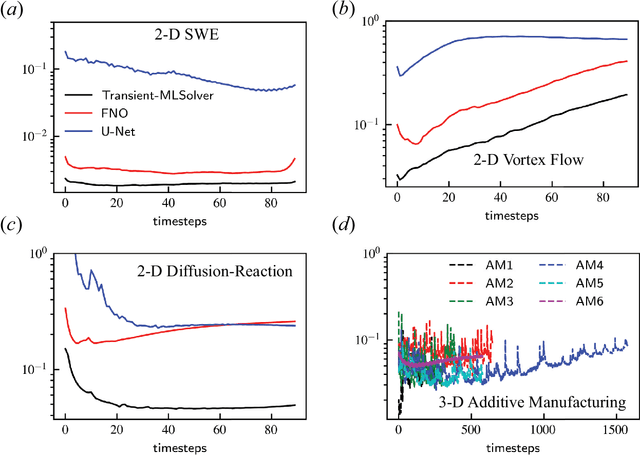
In this paper, we propose a domain-decomposition-based deep learning (DL) framework, named transient-CoMLSim, for accurately modeling unsteady and nonlinear partial differential equations (PDEs). The framework consists of two key components: (a) a convolutional neural network (CNN)-based autoencoder architecture and (b) an autoregressive model composed of fully connected layers. Unlike existing state-of-the-art methods that operate on the entire computational domain, our CNN-based autoencoder computes a lower-dimensional basis for solution and condition fields represented on subdomains. Timestepping is performed entirely in the latent space, generating embeddings of the solution variables from the time history of embeddings of solution and condition variables. This approach not only reduces computational complexity but also enhances scalability, making it well-suited for large-scale simulations. Furthermore, to improve the stability of our rollouts, we employ a curriculum learning (CL) approach during the training of the autoregressive model. The domain-decomposition strategy enables scaling to out-of-distribution domain sizes while maintaining the accuracy of predictions -- a feature not easily integrated into popular DL-based approaches for physics simulations. We benchmark our model against two widely-used DL architectures, Fourier Neural Operator (FNO) and U-Net, and demonstrate that our framework outperforms them in terms of accuracy, extrapolation to unseen timesteps, and stability for a wide range of use cases.

StressGAN: A Generative Deep Learning Model for 2D Stress Distribution Prediction

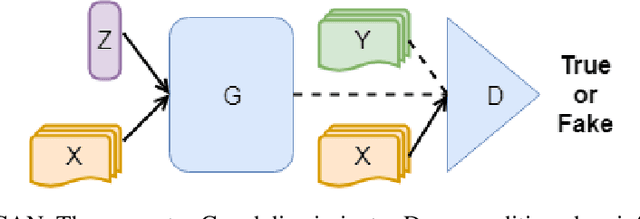
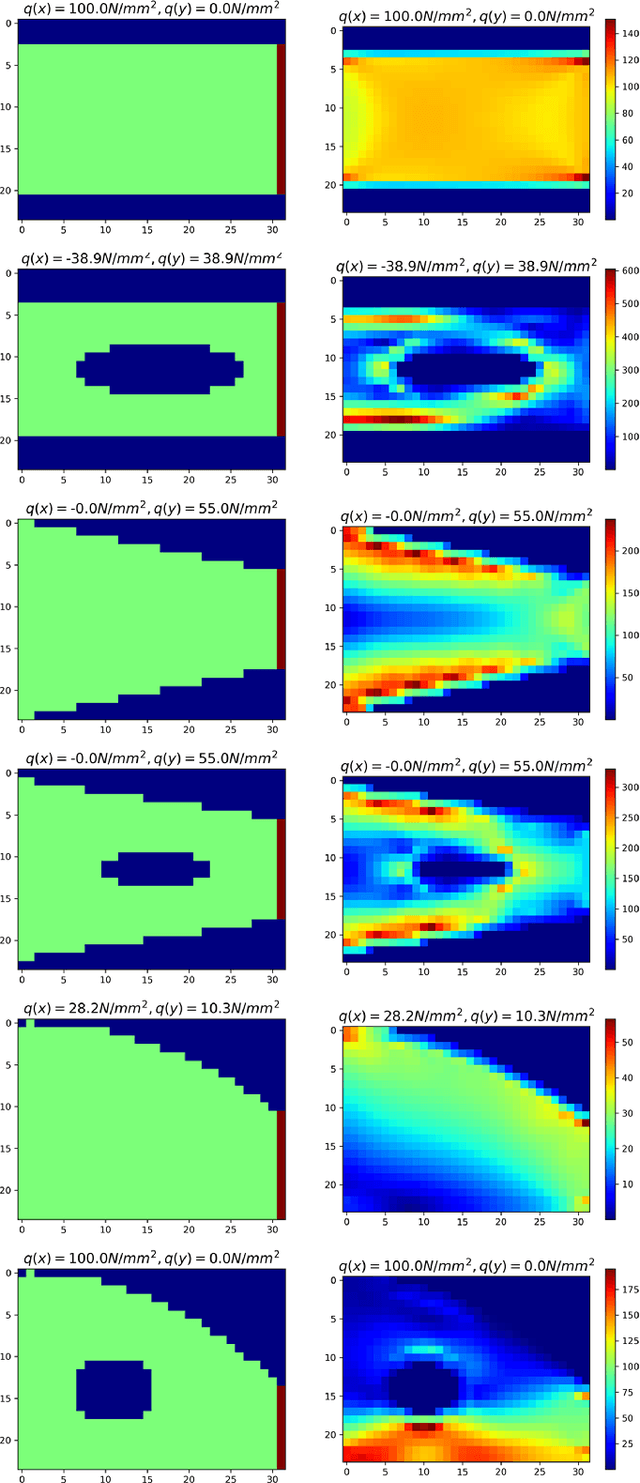
Using deep learning to analyze mechanical stress distributions has been gaining interest with the demand for fast stress analysis methods. Deep learning approaches have achieved excellent outcomes when utilized to speed up stress computation and learn the physics without prior knowledge of underlying equations. However, most studies restrict the variation of geometry or boundary conditions, making these methods difficult to be generalized to unseen configurations. We propose a conditional generative adversarial network (cGAN) model for predicting 2D von Mises stress distributions in solid structures. The cGAN learns to generate stress distributions conditioned by geometries, load, and boundary conditions through a two-player minimax game between two neural networks with no prior knowledge. By evaluating the generative network on two stress distribution datasets under multiple metrics, we demonstrate that our model can predict more accurate high-resolution stress distributions than a baseline convolutional neural network model, given various and complex cases of geometry, load and boundary conditions.

TopologyGAN: Topology Optimization Using Generative Adversarial Networks Based on Physical Fields Over the Initial Domain

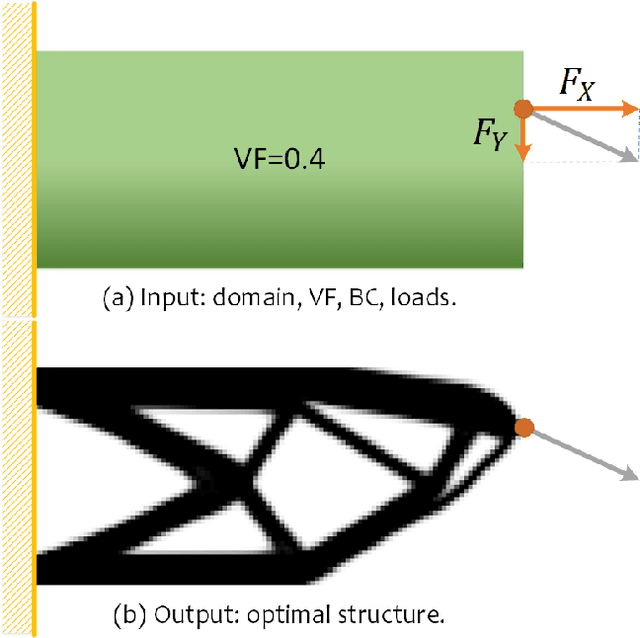
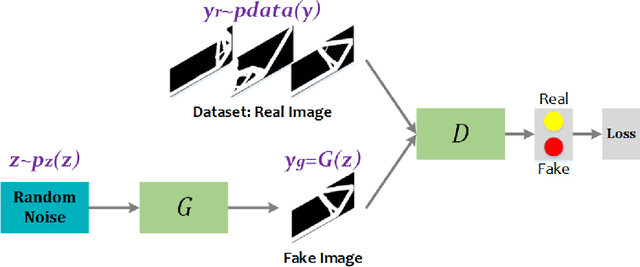
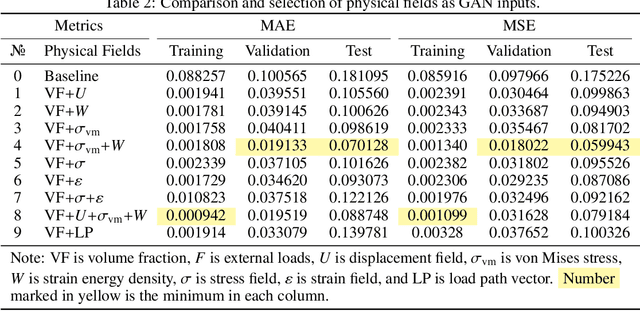
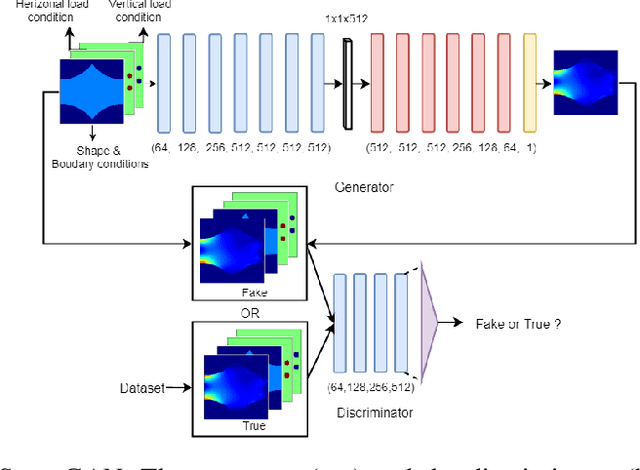
In topology optimization using deep learning, load and boundary conditions represented as vectors or sparse matrices often miss the opportunity to encode a rich view of the design problem, leading to less than ideal generalization results. We propose a new data-driven topology optimization model called TopologyGAN that takes advantage of various physical fields computed on the original, unoptimized material domain, as inputs to the generator of a conditional generative adversarial network (cGAN). Compared to a baseline cGAN, TopologyGAN achieves a nearly $3\times$ reduction in the mean squared error and a $2.5\times$ reduction in the mean absolute error on test problems involving previously unseen boundary conditions. Built on several existing network models, we also introduce a hybrid network called U-SE(Squeeze-and-Excitation)-ResNet for the generator that further increases the overall accuracy. We publicly share our full implementation and trained network.

3D Shape Synthesis for Conceptual Design and Optimization Using Variational Autoencoders

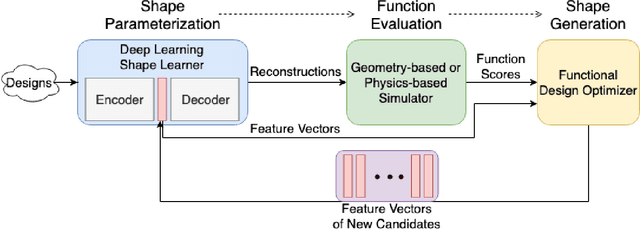
We propose a data-driven 3D shape design method that can learn a generative model from a corpus of existing designs, and use this model to produce a wide range of new designs. The approach learns an encoding of the samples in the training corpus using an unsupervised variational autoencoder-decoder architecture, without the need for an explicit parametric representation of the original designs. To facilitate the generation of smooth final surfaces, we develop a 3D shape representation based on a distance transformation of the original 3D data, rather than using the commonly utilized binary voxel representation. Once established, the generator maps the latent space representations to the high-dimensional distance transformation fields, which are then automatically surfaced to produce 3D representations amenable to physics simulations or other objective function evaluation modules. We demonstrate our approach for the computational design of gliders that are optimized to attain prescribed performance scores. Our results show that when combined with genetic optimization, the proposed approach can generate a rich set of candidate concept designs that achieve prescribed functional goals, even when the original dataset has only a few or no solutions that achieve these goals.

Deep Learning for Stress Field Prediction Using Convolutional Neural Networks

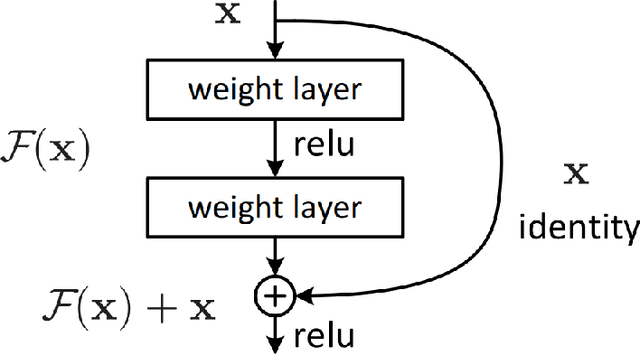
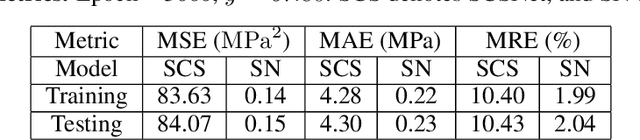
This research presents a deep learning based approach to predict stress fields in the solid material elastic deformation using convolutional neural networks (CNN). Two different architectures are proposed to solve the problem. One is Feature Representation embedded Convolutional Neural Network (FR-CNN) with a single input channel, and the other is Squeeze-and-Excitation Residual network modules embedded Fully Convolutional Neural network (SE-Res-FCN) with multiple input channels. Both the tow architectures are stable and converged reliably in training and testing on GPUs. Accuracy analysis shows that SE-Res-FCN has a significantly smaller mean squared error (MSE) and mean absolute error (MAE) than FR-CNN. Mean relative error (MRE) of the SE-Res-FCN model is about 0.25% with respect to the average ground truth. The validation results indicate that the SE-Res-FCN model can accurately predict the stress field. For stress field prediction, the hierarchical architecture becomes deeper within certain limits, and then its prediction becomes more accurate. Fully trained deep learning models have higher computational efficiency over conventional FEM models, so they have great foreground and potential in structural design and topology optimization.

3D Conceptual Design Using Deep Learning

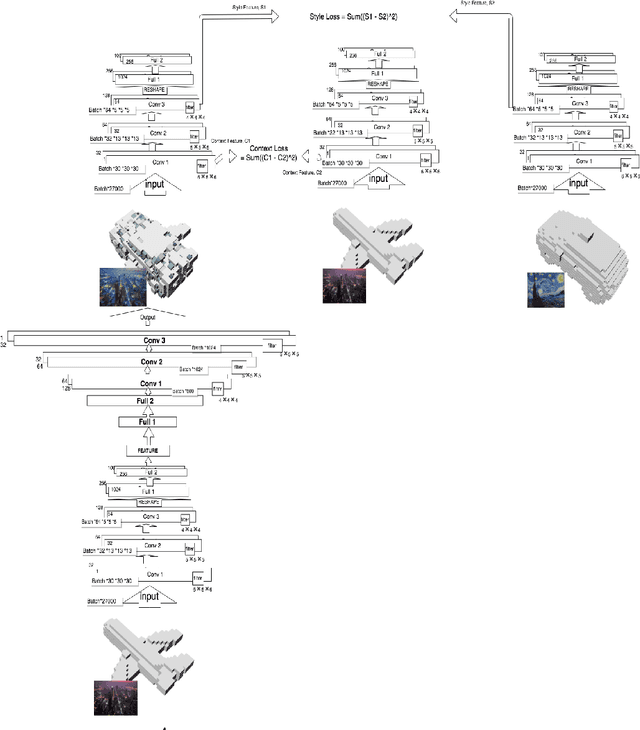
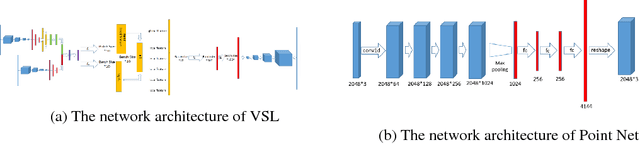
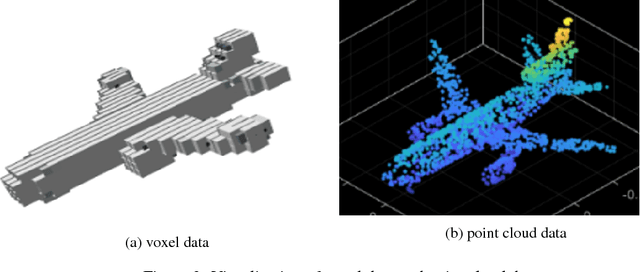
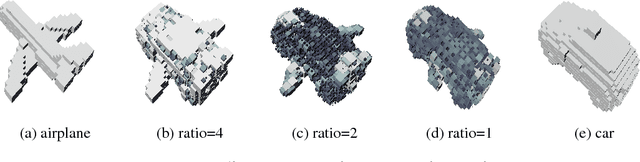
This article proposes a data-driven methodology to achieve a fast design support, in order to generate or develop novel designs covering multiple object categories. This methodology implements two state-of-the-art Variational Autoencoder dealing with 3D model data. Our methodology constructs a self-defined loss function. The loss function, containing the outputs of certain layers in the autoencoder, obtains combination of different latent features from different 3D model categories. Additionally, this article provide detail explanation to utilize the Princeton ModelNet40 database, a comprehensive clean collection of 3D CAD models for objects. After convert the original 3D mesh file to voxel and point cloud data type, we enable to feed our autoencoder with data of the same size of dimension. The novelty of this work is to leverage the power of deep learning methods as an efficient latent feature extractor to explore unknown designing areas. Through this project, we expect the output can show a clear and smooth interpretation of model from different categories to develop a fast design support to generate novel shapes. This final report will explore 1) the theoretical ideas, 2) the progresses to implement Variantional Autoencoder to attain implicit features from input shapes, 3) the results of output shapes during training in selected domains of both 3D voxel data and 3D point cloud data, and 4) our conclusion and future work to achieve the more outstanding goal.

Data-driven Upsampling of Point Clouds

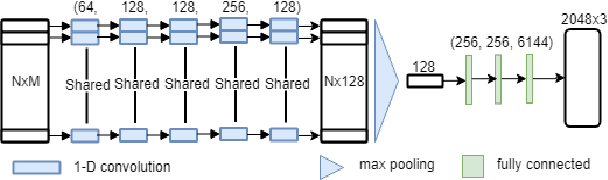
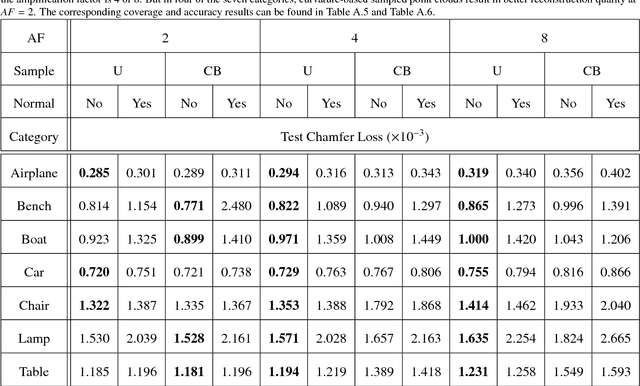
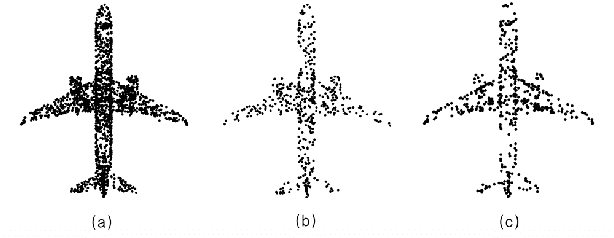
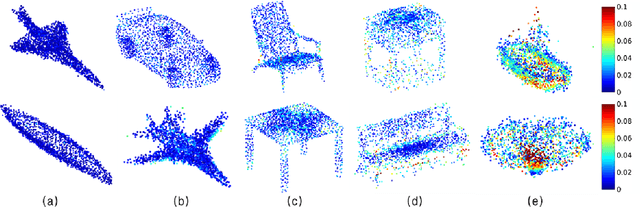
High quality upsampling of sparse 3D point clouds is critically useful for a wide range of geometric operations such as reconstruction, rendering, meshing, and analysis. In this paper, we propose a data-driven algorithm that enables an upsampling of 3D point clouds without the need for hard-coded rules. Our approach uses a deep network with Chamfer distance as the loss function, capable of learning the latent features in point clouds belonging to different object categories. We evaluate our algorithm across different amplification factors, with upsampling learned and performed on objects belonging to the same category as well as different categories. We also explore the desirable characteristics of input point clouds as a function of the distribution of the point samples. Finally, we demonstrate the performance of our algorithm in single-category training versus multi-category training scenarios. The final proposed model is compared against a baseline, optimization-based upsampling method. Results indicate that our algorithm is capable of generating more uniform and accurate upsamplings.