A domain decomposition-based autoregressive deep learning model for unsteady and nonlinear partial differential equations

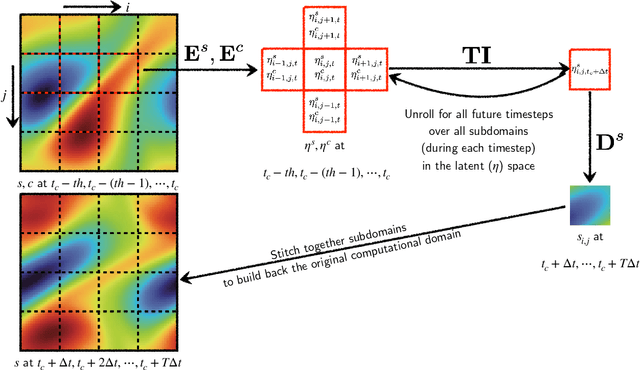
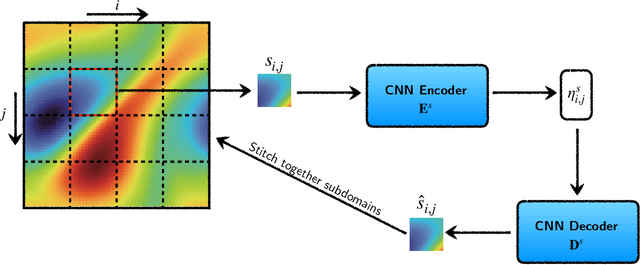
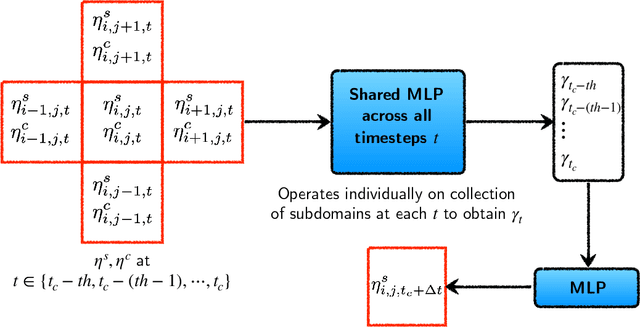
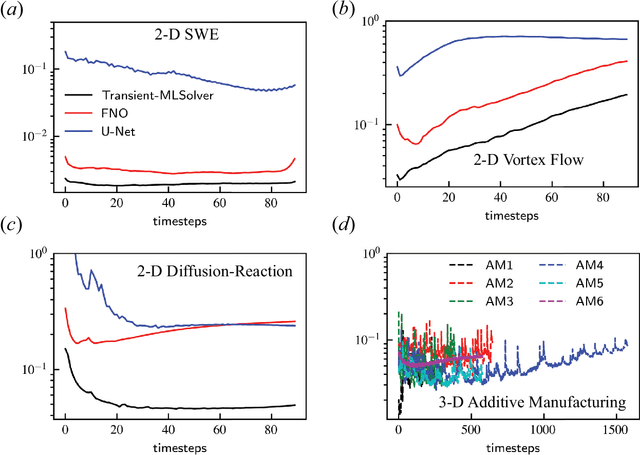
In this paper, we propose a domain-decomposition-based deep learning (DL) framework, named transient-CoMLSim, for accurately modeling unsteady and nonlinear partial differential equations (PDEs). The framework consists of two key components: (a) a convolutional neural network (CNN)-based autoencoder architecture and (b) an autoregressive model composed of fully connected layers. Unlike existing state-of-the-art methods that operate on the entire computational domain, our CNN-based autoencoder computes a lower-dimensional basis for solution and condition fields represented on subdomains. Timestepping is performed entirely in the latent space, generating embeddings of the solution variables from the time history of embeddings of solution and condition variables. This approach not only reduces computational complexity but also enhances scalability, making it well-suited for large-scale simulations. Furthermore, to improve the stability of our rollouts, we employ a curriculum learning (CL) approach during the training of the autoregressive model. The domain-decomposition strategy enables scaling to out-of-distribution domain sizes while maintaining the accuracy of predictions -- a feature not easily integrated into popular DL-based approaches for physics simulations. We benchmark our model against two widely-used DL architectures, Fourier Neural Operator (FNO) and U-Net, and demonstrate that our framework outperforms them in terms of accuracy, extrapolation to unseen timesteps, and stability for a wide range of use cases.

Sampling-based Distributed Training with Message Passing Neural Network

In this study, we introduce a domain-decomposition-based distributed training and inference approach for message-passing neural networks (MPNN). Our objective is to address the challenge of scaling edge-based graph neural networks as the number of nodes increases. Through our distributed training approach, coupled with Nystr\"om-approximation sampling techniques, we present a scalable graph neural network, referred to as DS-MPNN (D and S standing for distributed and sampled, respectively), capable of scaling up to $O(10^5)$ nodes. We validate our sampling and distributed training approach on two cases: (a) a Darcy flow dataset and (b) steady RANS simulations of 2-D airfoils, providing comparisons with both single-GPU implementation and node-based graph convolution networks (GCNs). The DS-MPNN model demonstrates comparable accuracy to single-GPU implementation, can accommodate a significantly larger number of nodes compared to the single-GPU variant (S-MPNN), and significantly outperforms the node-based GCN.

Diffusion model based data generation for partial differential equations

In a preliminary attempt to address the problem of data scarcity in physics-based machine learning, we introduce a novel methodology for data generation in physics-based simulations. Our motivation is to overcome the limitations posed by the limited availability of numerical data. To achieve this, we leverage a diffusion model that allows us to generate synthetic data samples and test them for two canonical cases: (a) the steady 2-D Poisson equation, and (b) the forced unsteady 2-D Navier-Stokes (NS) {vorticity-transport} equation in a confined box. By comparing the generated data samples against outputs from classical solvers, we assess their accuracy and examine their adherence to the underlying physics laws. In this way, we emphasize the importance of not only satisfying visual and statistical comparisons with solver data but also ensuring the generated data's conformity to physics laws, thus enabling their effective utilization in downstream tasks.