Causal machine learning for single-cell genomics

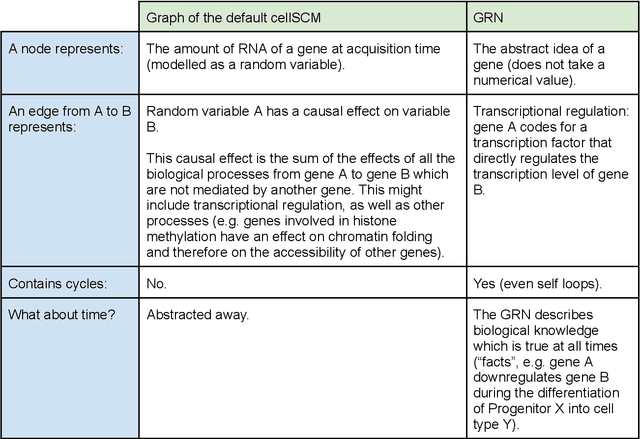
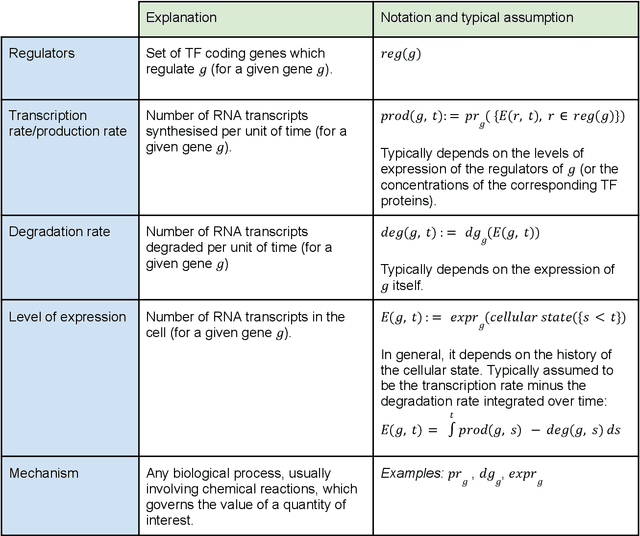
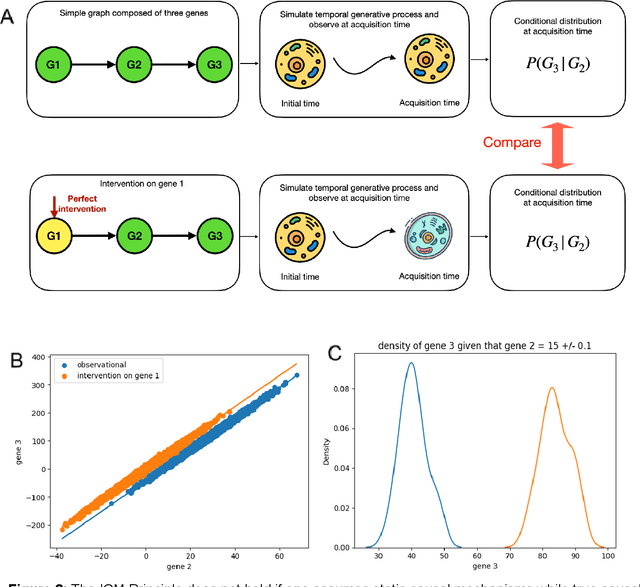
Advances in single-cell omics allow for unprecedented insights into the transcription profiles of individual cells. When combined with large-scale perturbation screens, through which specific biological mechanisms can be targeted, these technologies allow for measuring the effect of targeted perturbations on the whole transcriptome. These advances provide an opportunity to better understand the causative role of genes in complex biological processes such as gene regulation, disease progression or cellular development. However, the high-dimensional nature of the data, coupled with the intricate complexity of biological systems renders this task nontrivial. Within the machine learning community, there has been a recent increase of interest in causality, with a focus on adapting established causal techniques and algorithms to handle high-dimensional data. In this perspective, we delineate the application of these methodologies within the realm of single-cell genomics and their challenges. We first present the model that underlies most of current causal approaches to single-cell biology and discuss and challenge the assumptions it entails from the biological point of view. We then identify open problems in the application of causal approaches to single-cell data: generalising to unseen environments, learning interpretable models, and learning causal models of dynamics. For each problem, we discuss how various research directions - including the development of computational approaches and the adaptation of experimental protocols - may offer ways forward, or on the contrary pose some difficulties. With the advent of single cell atlases and increasing perturbation data, we expect causal models to become a crucial tool for informed experimental design.

Conditionally Invariant Representation Learning for Disentangling Cellular Heterogeneity

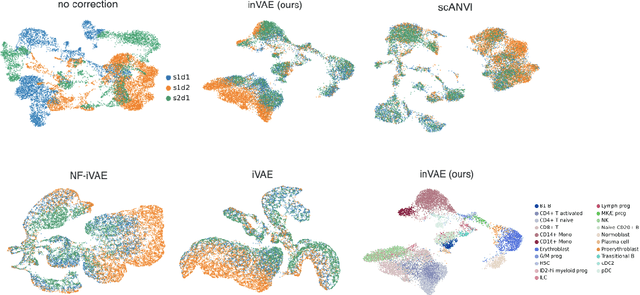
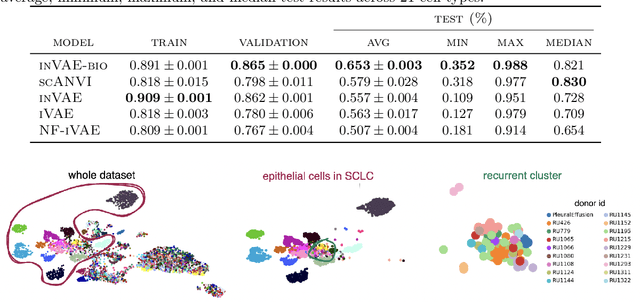
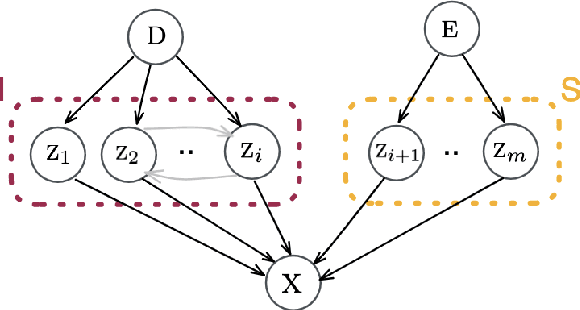
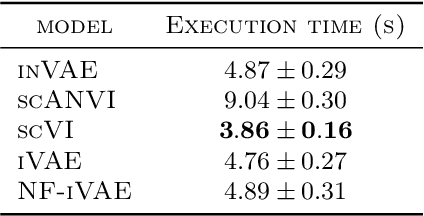
This paper presents a novel approach that leverages domain variability to learn representations that are conditionally invariant to unwanted variability or distractors. Our approach identifies both spurious and invariant latent features necessary for achieving accurate reconstruction by placing distinct conditional priors on latent features. The invariant signals are disentangled from noise by enforcing independence which facilitates the construction of an interpretable model with a causal semantic. By exploiting the interplay between data domains and labels, our method simultaneously identifies invariant features and builds invariant predictors. We apply our method to grand biological challenges, such as data integration in single-cell genomics with the aim of capturing biological variations across datasets with many samples, obtained from different conditions or multiple laboratories. Our approach allows for the incorporation of specific biological mechanisms, including gene programs, disease states, or treatment conditions into the data integration process, bridging the gap between the theoretical assumptions and real biological applications. Specifically, the proposed approach helps to disentangle biological signals from data biases that are unrelated to the target task or the causal explanation of interest. Through extensive benchmarking using large-scale human hematopoiesis and human lung cancer data, we validate the superiority of our approach over existing methods and demonstrate that it can empower deeper insights into cellular heterogeneity and the identification of disease cell states.

Sparsity in Continuous-Depth Neural Networks

Neural Ordinary Differential Equations (NODEs) have proven successful in learning dynamical systems in terms of accurately recovering the observed trajectories. While different types of sparsity have been proposed to improve robustness, the generalization properties of NODEs for dynamical systems beyond the observed data are underexplored. We systematically study the influence of weight and feature sparsity on forecasting as well as on identifying the underlying dynamical laws. Besides assessing existing methods, we propose a regularization technique to sparsify "input-output connections" and extract relevant features during training. Moreover, we curate real-world datasets consisting of human motion capture and human hematopoiesis single-cell RNA-seq data to realistically analyze different levels of out-of-distribution (OOD) generalization in forecasting and dynamics identification respectively. Our extensive empirical evaluation on these challenging benchmarks suggests that weight sparsity improves generalization in the presence of noise or irregular sampling. However, it does not prevent learning spurious feature dependencies in the inferred dynamics, rendering them impractical for predictions under interventions, or for inferring the true underlying dynamics. Instead, feature sparsity can indeed help with recovering sparse ground-truth dynamics compared to unregularized NODEs.

Beyond Predictions in Neural ODEs: Identification and Interventions

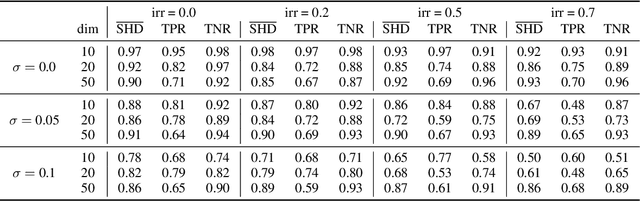
Spurred by tremendous success in pattern matching and prediction tasks, researchers increasingly resort to machine learning to aid original scientific discovery. Given large amounts of observational data about a system, can we uncover the rules that govern its evolution? Solving this task holds the great promise of fully understanding the causal interactions and being able to make reliable predictions about the system's behavior under interventions. We take a step towards answering this question for time-series data generated from systems of ordinary differential equations (ODEs). While the governing ODEs might not be identifiable from data alone, we show that combining simple regularization schemes with flexible neural ODEs can robustly recover the dynamics and causal structures from time-series data. Our results on a variety of (non)-linear first and second order systems as well as real data validate our method. We conclude by showing that we can also make accurate predictions under interventions on variables or the system itself.