Can LLMs Refuse Questions They Do Not Know? Measuring Knowledge-Aware Refusal in Factual Tasks

Large Language Models (LLMs) should refuse to answer questions beyond their knowledge. This capability, which we term knowledge-aware refusal, is crucial for factual reliability. However, existing metrics fail to faithfully measure this ability. On the one hand, simple refusal-based metrics are biased by refusal rates and yield inconsistent scores when models exhibit different refusal tendencies. On the other hand, existing calibration metrics are proxy-based, capturing the performance of auxiliary calibration processes rather than the model's actual refusal behavior. In this work, we propose the Refusal Index (RI), a principled metric that measures how accurately LLMs refuse questions they do not know. We define RI as Spearman's rank correlation between refusal probability and error probability. To make RI practically measurable, we design a lightweight two-pass evaluation method that efficiently estimates RI from observed refusal rates across two standard evaluation runs. Extensive experiments across 16 models and 5 datasets demonstrate that RI accurately quantifies a model's intrinsic knowledge-aware refusal capability in factual tasks. Notably, RI remains stable across different refusal rates and provides consistent model rankings independent of a model's overall accuracy and refusal rates. More importantly, RI provides insight into an important but previously overlooked aspect of LLM factuality: while LLMs achieve high accuracy on factual tasks, their refusal behavior can be unreliable and fragile. This finding highlights the need to complement traditional accuracy metrics with the Refusal Index for comprehensive factuality evaluation.

Breaking the Context Bottleneck on Long Time Series Forecasting

Long-term time-series forecasting is essential for planning and decision-making in economics, energy, and transportation, where long foresight is required. To obtain such long foresight, models must be both efficient and effective in processing long sequence. Recent advancements have enhanced the efficiency of these models; however, the challenge of effectively leveraging longer sequences persists. This is primarily due to the tendency of these models to overfit when presented with extended inputs, necessitating the use of shorter input lengths to maintain tolerable error margins. In this work, we investigate the multiscale modeling method and propose the Logsparse Decomposable Multiscaling (LDM) framework for the efficient and effective processing of long sequences. We demonstrate that by decoupling patterns at different scales in time series, we can enhance predictability by reducing non-stationarity, improve efficiency through a compact long input representation, and simplify the architecture by providing clear task assignments. Experimental results demonstrate that LDM not only outperforms all baselines in long-term forecasting benchmarks, but also reducing both training time and memory costs.

Do Contemporary CATE Models Capture Real-World Heterogeneity? Findings from a Large-Scale Benchmark

We present unexpected findings from a large-scale benchmark study evaluating Conditional Average Treatment Effect (CATE) estimation algorithms. By running 16 modern CATE models across 43,200 datasets, we find that: (a) 62\% of CATE estimates have a higher Mean Squared Error (MSE) than a trivial zero-effect predictor, rendering them ineffective; (b) in datasets with at least one useful CATE estimate, 80\% still have higher MSE than a constant-effect model; and (c) Orthogonality-based models outperform other models only 30\% of the time, despite widespread optimism about their performance. These findings expose significant limitations in current CATE models and suggest ample opportunities for further research. Our findings stem from a novel application of \textit{observational sampling}, originally developed to evaluate Average Treatment Effect (ATE) estimates from observational methods with experiment data. To adapt observational sampling for CATE evaluation, we introduce a statistical parameter, $Q$, equal to MSE minus a constant and preserves the ranking of models by their MSE. We then derive a family of sample statistics, collectively called $\hat{Q}$, that can be computed from real-world data. We prove that $\hat{Q}$ is a consistent estimator of $Q$ under mild technical conditions. When used in observational sampling, $\hat{Q}$ is unbiased and asymptotically selects the model with the smallest MSE. To ensure the benchmark reflects real-world heterogeneity, we handpick datasets where outcomes come from field rather than simulation. By combining the new observational sampling method, new statistics, and real-world datasets, the benchmark provides a unique perspective on CATE estimator performance and uncover gaps in capturing real-world heterogeneity.

QDA-SQL: Questions Enhanced Dialogue Augmentation for Multi-Turn Text-to-SQL

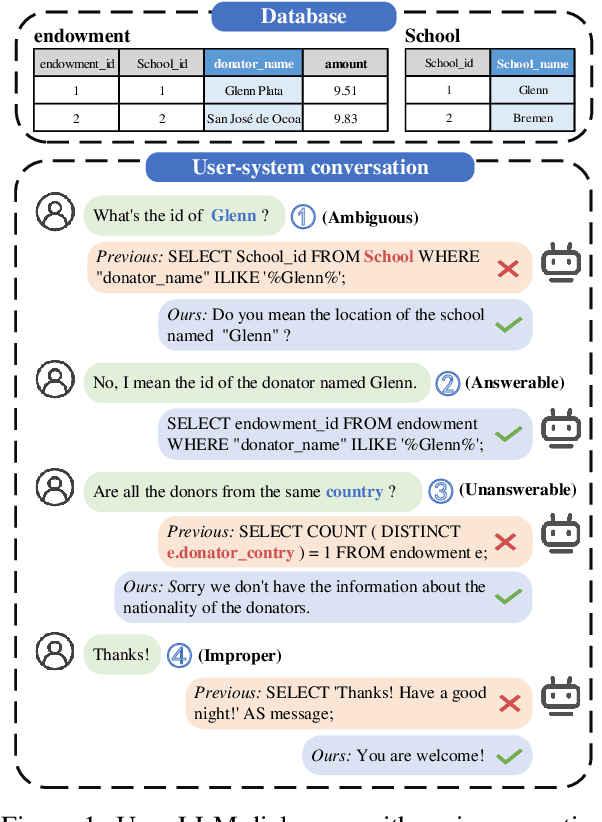
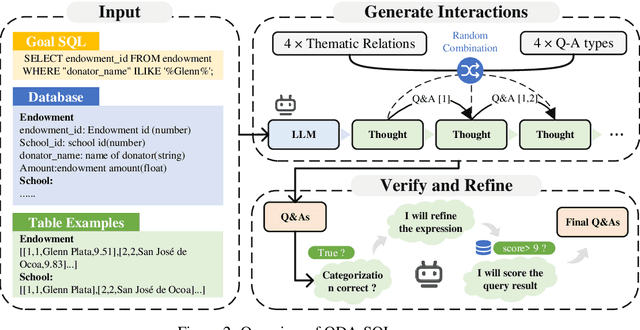
Fine-tuning large language models (LLMs) for specific domain tasks has achieved great success in Text-to-SQL tasks. However, these fine-tuned models often face challenges with multi-turn Text-to-SQL tasks caused by ambiguous or unanswerable questions. It is desired to enhance LLMs to handle multiple types of questions in multi-turn Text-to-SQL tasks. To address this, we propose a novel data augmentation method, called QDA-SQL, which generates multiple types of multi-turn Q\&A pairs by using LLMs. In QDA-SQL, we introduce a novel data augmentation method incorporating validation and correction mechanisms to handle complex multi-turn Text-to-SQL tasks. Experimental results demonstrate that QDA-SQL enables fine-tuned models to exhibit higher performance on SQL statement accuracy and enhances their ability to handle complex, unanswerable questions in multi-turn Text-to-SQL tasks. The generation script and test set are released at https://github.com/mcxiaoxiao/QDA-SQL.