Hai Min
GUN: Gradual Upsampling Network for Single Image Super-Resolution
Jul 04, 2018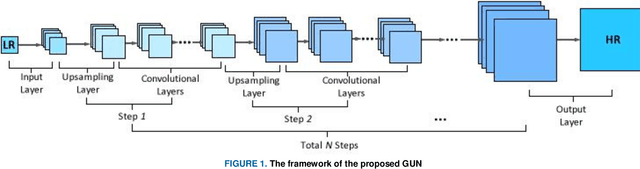

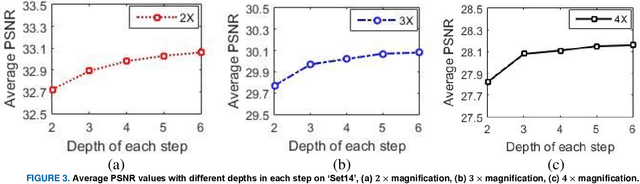
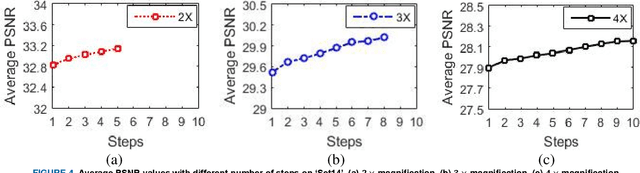
Abstract:In this paper, an efficient super-resolution (SR) method based on deep convolutional neural network (CNN) is proposed, namely Gradual Upsampling Network (GUN). Recent CNN based SR methods often preliminarily magnify the low resolution (LR) input to high resolution (HR) and then reconstruct the HR input, or directly reconstruct the LR input and then recover the HR result at the last layer. The proposed GUN utilizes a gradual process instead of these two commonly used frameworks. The GUN consists of an input layer, multiple upsampling and convolutional layers, and an output layer. By means of the gradual process, the proposed network can simplify the direct SR problem to multistep easier upsampling tasks with very small magnification factor in each step. Furthermore, a gradual training strategy is presented for the GUN. In the proposed training process, an initial network can be easily trained with edge-like samples, and then the weights are gradually tuned with more complex samples. The GUN can recover fine and vivid results, and is easy to be trained. The experimental results on several image sets demonstrate the effectiveness of the proposed network.
Robust and Efficient Subspace Segmentation via Least Squares Regression
Apr 27, 2014
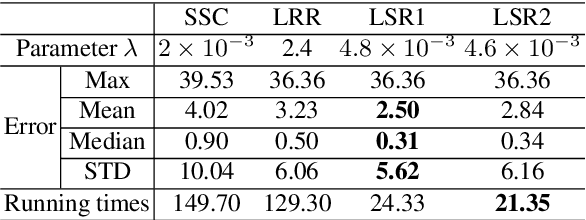
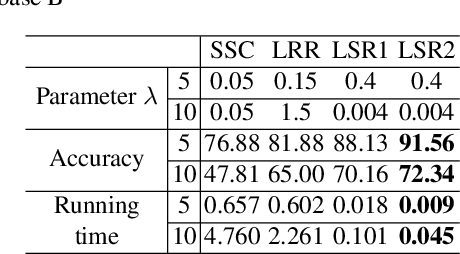
Abstract:This paper studies the subspace segmentation problem which aims to segment data drawn from a union of multiple linear subspaces. Recent works by using sparse representation, low rank representation and their extensions attract much attention. If the subspaces from which the data drawn are independent or orthogonal, they are able to obtain a block diagonal affinity matrix, which usually leads to a correct segmentation. The main differences among them are their objective functions. We theoretically show that if the objective function satisfies some conditions, and the data are sufficiently drawn from independent subspaces, the obtained affinity matrix is always block diagonal. Furthermore, the data sampling can be insufficient if the subspaces are orthogonal. Some existing methods are all special cases. Then we present the Least Squares Regression (LSR) method for subspace segmentation. It takes advantage of data correlation, which is common in real data. LSR encourages a grouping effect which tends to group highly correlated data together. Experimental results on the Hopkins 155 database and Extended Yale Database B show that our method significantly outperforms state-of-the-art methods. Beyond segmentation accuracy, all experiments demonstrate that LSR is much more efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge