Optimal Resource Allocation for ML Model Training and Deployment under Concept Drift

We study how to allocate resources for training and deployment of machine learning (ML) models under concept drift and limited budgets. We consider a setting in which a model provider distributes trained models to multiple clients whose devices support local inference but lack the ability to retrain those models, placing the burden of performance maintenance on the provider. We introduce a model-agnostic framework that captures the interaction between resource allocation, concept drift dynamics, and deployment timing. We show that optimal training policies depend critically on the aging properties of concept durations. Under sudden concept changes, we derive optimal training policies subject to budget constraints when concept durations follow distributions with Decreasing Mean Residual Life (DMRL), and show that intuitive heuristics are provably suboptimal under Increasing Mean Residual Life (IMRL). We further study model deployment under communication constraints, prove that the associated optimization problem is quasi-convex under mild conditions, and propose a randomized scheduling strategy that achieves near-optimal client-side performance. These results offer theoretical and algorithmic foundations for cost-efficient ML model management under concept drift, with implications for continual learning, distributed inference, and adaptive ML systems.

Importance Sampling via Score-based Generative Models

Importance sampling, which involves sampling from a probability density function (PDF) proportional to the product of an importance weight function and a base PDF, is a powerful technique with applications in variance reduction, biased or customized sampling, data augmentation, and beyond. Inspired by the growing availability of score-based generative models (SGMs), we propose an entirely training-free Importance sampling framework that relies solely on an SGM for the base PDF. Our key innovation is realizing the importance sampling process as a backward diffusion process, expressed in terms of the score function of the base PDF and the specified importance weight function--both readily available--eliminating the need for any additional training. We conduct a thorough analysis demonstrating the method's scalability and effectiveness across diverse datasets and tasks, including importance sampling for industrial and natural images with neural importance weight functions. The training-free aspect of our method is particularly compelling in real-world scenarios where a single base distribution underlies multiple biased sampling tasks, each requiring a different importance weight function. To the best of our knowledge our approach is the first importance sampling framework to achieve this.

Network Adaptive Federated Learning: Congestion and Lossy Compression

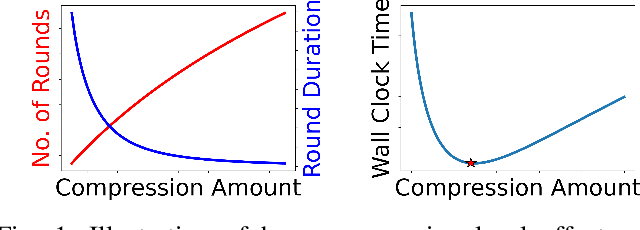
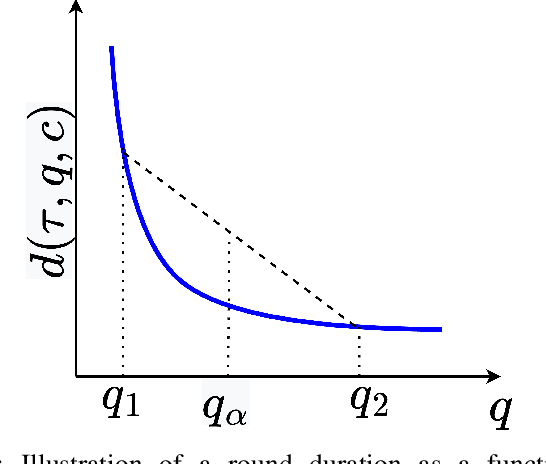
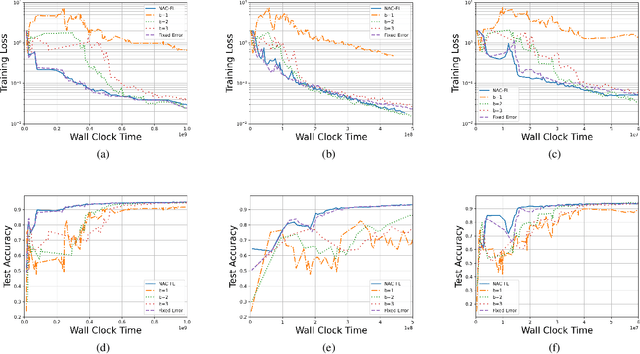
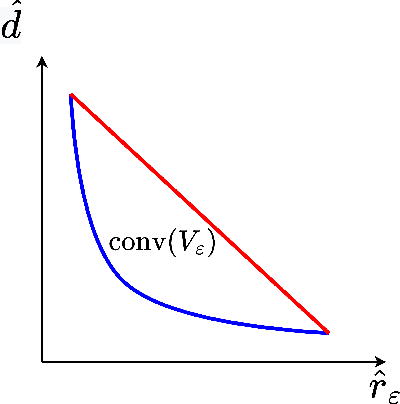
In order to achieve the dual goals of privacy and learning across distributed data, Federated Learning (FL) systems rely on frequent exchanges of large files (model updates) between a set of clients and the server. As such FL systems are exposed to, or indeed the cause of, congestion across a wide set of network resources. Lossy compression can be used to reduce the size of exchanged files and associated delays, at the cost of adding noise to model updates. By judiciously adapting clients' compression to varying network congestion, an FL application can reduce wall clock training time. To that end, we propose a Network Adaptive Compression (NAC-FL) policy, which dynamically varies the client's lossy compression choices to network congestion variations. We prove, under appropriate assumptions, that NAC-FL is asymptotically optimal in terms of directly minimizing the expected wall clock training time. Further, we show via simulation that NAC-FL achieves robust performance improvements with higher gains in settings with positively correlated delays across time.

Stochastic-Greedy++: Closing the Optimality Gap in Exact Weak Submodular Maximization

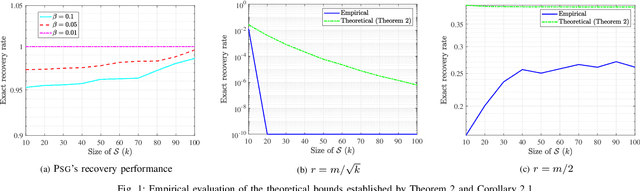
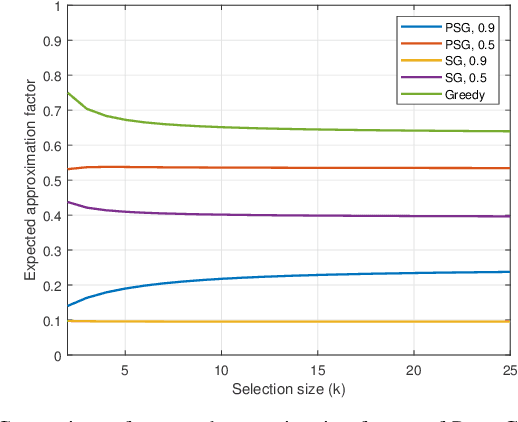
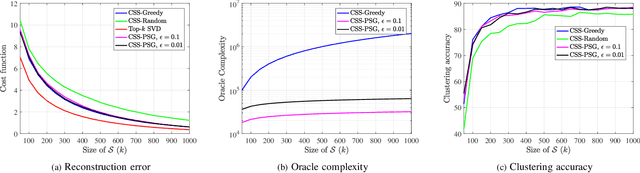
Many problems in discrete optimization can be formulated as the task of maximizing a monotone and weak submodular function subject to a cardinality constraint. For such problems, a simple greedy algorithm is guaranteed to find a solution with a value no worse than $1-1/e$ of the optimal. Although the computational complexity of Greedy is linear in the size of the data $m$ and cardinality constraint ($k$), even this linear complexity becomes prohibitive for large-scale datasets. Recently, Mirzasoleyman et al. propose a randomized greedy algorithm, Stochastic-Greedy, with the expected worst case approximation ratio of $1-1/e-\epsilon$ where $0<\epsilon<1$ is a parameter controlling the trade-off between complexity and performance. We consider the following question: Given the small $\epsilon$ gap between the worst-case performance guarantees of Stochastic-Greedy and Greedy, can we expect nearly equivalent conditions for the exact identification of the optimal subset? In this paper we show that in general there is an unbounded gap between the exact performance of Stochastic-Greedy and Greedy by considering the problem of sparse support selection. Tropp and Gilbert show Greedy finds the optimal solution with high probability assuming $n=O(k\log\frac{m}{k})$, the information theoretic lowerbound on minimum number of measurements for exact identification of the optimal subset. By contrast, we show that irrespective of the number of measurements, Stochastic-Greedy with overwhelming probability fails to find the optimal subset. We reveal that the failure of Stochastic-Greedy can be circumvented by progressively increasing the size of the stochastic search space. Employing this insight, we present the first sparse support selection algorithm that achieves exact identification of the optimal subset from $O(k\log\frac{m}{k})$ measurements with complexity $\tilde{O}(m)$ for arbitrary sparse vectors.

Modeling and Optimization of Human-machine Interaction Processes via the Maximum Entropy Principle

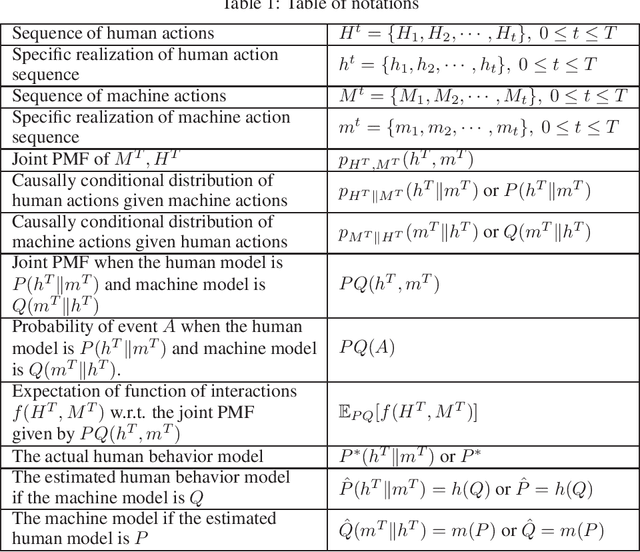
We propose a data-driven framework to enable the modeling and optimization of human-machine interaction processes, e.g., systems aimed at assisting humans in decision-making or learning, work-load allocation, and interactive advertising. This is a challenging problem for several reasons. First, humans' behavior is hard to model or infer, as it may reflect biases, long term memory, and sensitivity to sequencing, i.e., transience and exponential complexity in the length of the interaction. Second, due to the interactive nature of such processes, the machine policy used to engage with a human may bias possible data-driven inferences. Finally, in choosing machine policies that optimize interaction rewards, one must, on the one hand, avoid being overly sensitive to error/variability in the estimated human model, and on the other, being overly deterministic/predictable which may result in poor human 'engagement' in the interaction. To meet these challenges, we propose a robust approach, based on the maximum entropy principle, which iteratively estimates human behavior and optimizes the machine policy--Alternating Entropy-Reward Ascent (AREA) algorithm. We characterize AREA, in terms of its space and time complexity and convergence. We also provide an initial validation based on synthetic data generated by an established noisy nonlinear model for human decision-making.