Stochastic-Greedy++: Closing the Optimality Gap in Exact Weak Submodular Maximization

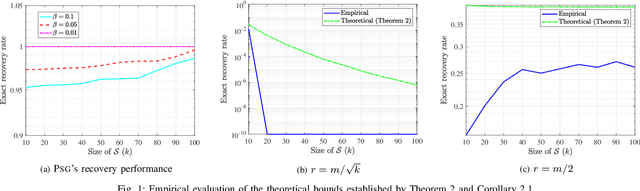
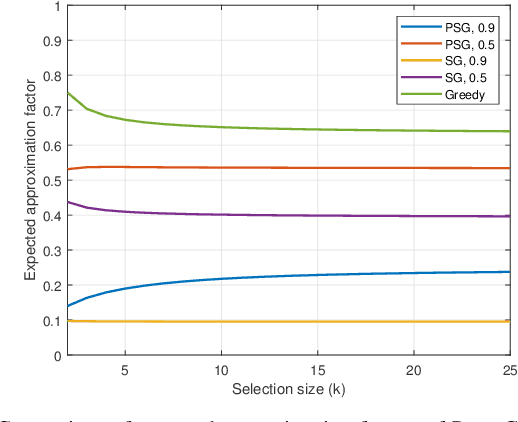
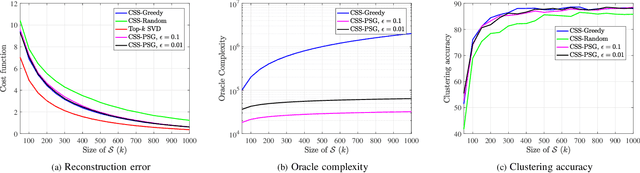
Many problems in discrete optimization can be formulated as the task of maximizing a monotone and weak submodular function subject to a cardinality constraint. For such problems, a simple greedy algorithm is guaranteed to find a solution with a value no worse than $1-1/e$ of the optimal. Although the computational complexity of Greedy is linear in the size of the data $m$ and cardinality constraint ($k$), even this linear complexity becomes prohibitive for large-scale datasets. Recently, Mirzasoleyman et al. propose a randomized greedy algorithm, Stochastic-Greedy, with the expected worst case approximation ratio of $1-1/e-\epsilon$ where $0<\epsilon<1$ is a parameter controlling the trade-off between complexity and performance. We consider the following question: Given the small $\epsilon$ gap between the worst-case performance guarantees of Stochastic-Greedy and Greedy, can we expect nearly equivalent conditions for the exact identification of the optimal subset? In this paper we show that in general there is an unbounded gap between the exact performance of Stochastic-Greedy and Greedy by considering the problem of sparse support selection. Tropp and Gilbert show Greedy finds the optimal solution with high probability assuming $n=O(k\log\frac{m}{k})$, the information theoretic lowerbound on minimum number of measurements for exact identification of the optimal subset. By contrast, we show that irrespective of the number of measurements, Stochastic-Greedy with overwhelming probability fails to find the optimal subset. We reveal that the failure of Stochastic-Greedy can be circumvented by progressively increasing the size of the stochastic search space. Employing this insight, we present the first sparse support selection algorithm that achieves exact identification of the optimal subset from $O(k\log\frac{m}{k})$ measurements with complexity $\tilde{O}(m)$ for arbitrary sparse vectors.