AttentionX: Exploiting Consensus Discrepancy In Attention from A Distributed Optimization Perspective

In this paper, we extend the standard Attention in transformer by exploiting the consensus discrepancy from a distributed optimization perspective, referred to as AttentionX. It is noted that the primal-dual method of multipliers (PDMM) \cite{Zhang16PDMM} is designed to iteratively solve a broad class of distributed optimization problems over a pear-to-pear (P2P) network, where neighbouring nodes gradually reach consensus as specified by predefined linear edge-constraints in the optimization process. In particular, at each iteration of PDMM, each node in a network first performs information-gathering from neighbours and then performs local information-fusion. From a high-level point of view, the $KQ$-softmax-based weighted summation of $V$-representations in Attention corresponds information-gathering from neighbours while the feature-processing via the feed-forward network (FFN) in transformer corresponds to local information fusion. PDMM exploits the Lagrangian multipliers to capture the historical consensus discrepancy in the form of residual errors of the linear edge-constraints, which plays a crucial role for the algorithm to converge. Inspired by PDMM, we propose AttentionX to incorporate the consensus discrepancy in the output update-expression of the standard Attention. The consensus discrepancy in AttentionX refers to the difference between the weighted summation of $V$-representations and scaled $V$-representions themselves. Experiments on ViT and nanoGPT show promising performance.

On Exact Bit-level Reversible Transformers Without Changing Architectures

In the literature, various reversible deep neural networks (DNN) models have been proposed to reduce memory consumption or improve data-throughput in the training process. However, almost all existing reversible DNNs either are constrained to have special structures or are constructed by modifying the original DNN architectures considerably to enable reversibility. In this work, we propose exact bit-level reversible transformers without changing the architectures in the inference procedure. The basic idea is to first treat each transformer block as the Euler integration approximation for solving an ordinary differential equation (ODE) and then incorporate the technique of bidirectional integration approximation (BDIA) (see [26]) for BDIA-based diffusion inversion) into the neural architecture together with activation quantization to make it exactly bit-level reversible, referred to as BDIA-transformer. In the training process, we let a hyper-parameter $\gamma$ in BDIA-transformer randomly take one of the two values $\{0.5, -0.5\}$ per transformer block for averaging two consecutive integration approximations, which regularizes the models for improving the validation accuracy. Light-weight side information per transformer block is required to be stored in the forward process to account for binary quantization loss to enable exact bit-level reversibility. In the inference procedure, the expectation $\mathbb{E}(\gamma)=0$ is taken to make the resulting architectures of BDIA-transformer be identical to transformers up to activation quantization. Empirical study indicates that BDIA-transformers outperform their original counterparts notably due to the regularization effect of the $\gamma$ parameter.

A Distributed Algorithm for Personal Sound Zones Systems

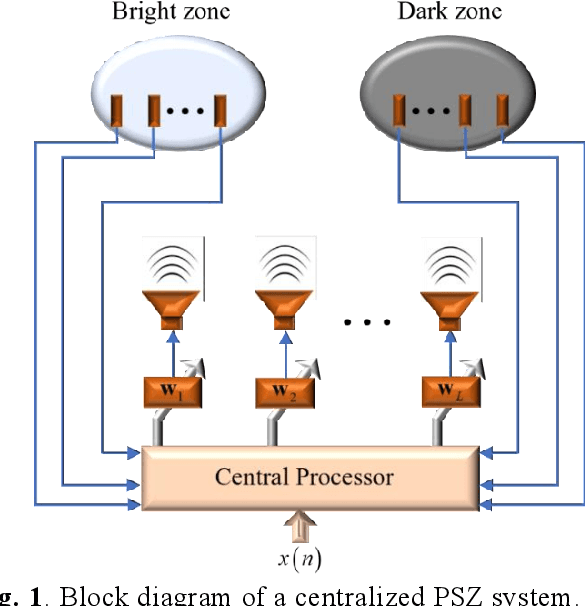
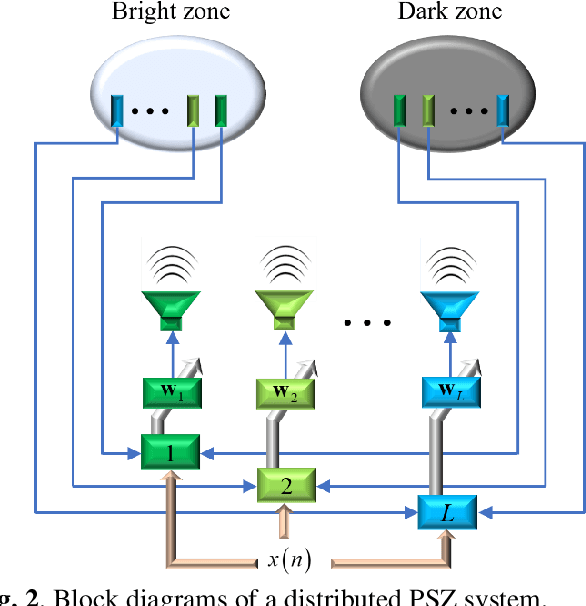
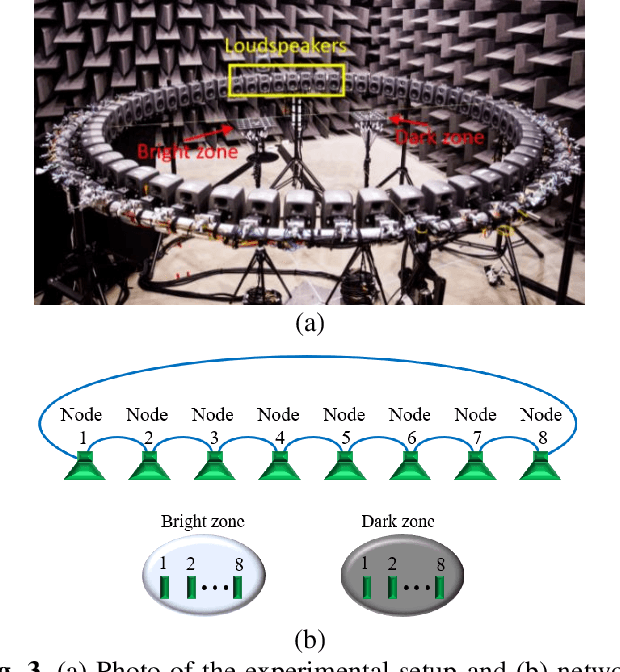
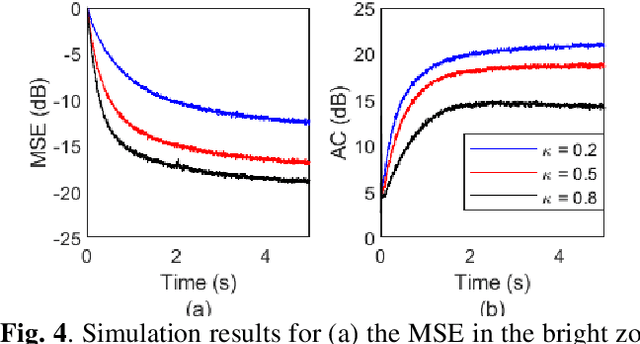
A Personal Sound Zones (PSZ) system aims to generate two or more independent listening zones that allow multiple users to listen to different music/audio content in a shared space without the need for wearing headphones. Most existing studies assume that the acoustic paths between loudspeakers and microphones are measured beforehand in a stationary environment. Recently, adaptive PSZ systems have been explored to adapt the system in a time-varying acoustic environment. However, because a PSZ system usually requires multiple loudspeakers, the multichannel adaptive algorithms impose a high computational load on the processor. To overcome that problem, this paper proposes an efficient distributed algorithm for PSZ systems, which not only spreads the computational burden over multiple nodes but also reduces the overall computational complexity, at the expense of a slight decrease in performance. Simulation results with true room impulse responses measured in a Hemi-Anechoic chamber are performed to verify the proposed distributed PSZ system.

Exact Diffusion Inversion via Bi-directional Integration Approximation

Recently, different methods have been proposed to address the inconsistency issue of DDIM inversion to enable image editing, such as EDICT \cite{Wallace23EDICT} and Null-text inversion \cite{Mokady23NullTestInv}. However, the above methods introduce considerable computational overhead. In this paper, we propose a new technique, named \emph{bi-directional integration approximation} (BDIA), to perform exact diffusion inversion with neglible computational overhead. Suppose we would like to estimate the next diffusion state $\boldsymbol{z}_{i-1}$ at timestep $t_i$ with the historical information $(i,\boldsymbol{z}_i)$ and $(i+1,\boldsymbol{z}_{i+1})$. We first obtain the estimated Gaussian noise $\hat{\boldsymbol{\epsilon}}(\boldsymbol{z}_i,i)$, and then apply the DDIM update procedure twice for approximating the ODE integration over the next time-slot $[t_i, t_{i-1}]$ in the forward manner and the previous time-slot $[t_i, t_{t+1}]$ in the backward manner. The DDIM step for the previous time-slot is used to refine the integration approximation made earlier when computing $\boldsymbol{z}_i$. One nice property with BDIA-DDIM is that the update expression for $\boldsymbol{z}_{i-1}$ is a linear combination of $(\boldsymbol{z}_{i+1}, \boldsymbol{z}_i, \hat{\boldsymbol{\epsilon}}(\boldsymbol{z}_i,i))$. This allows for exact backward computation of $\boldsymbol{z}_{i+1}$ given $(\boldsymbol{z}_i, \boldsymbol{z}_{i-1})$, thus leading to exact diffusion inversion. Experiments on both image reconstruction and image editing were conducted, confirming our statement. BDIA can also be applied to improve the performance of other ODE solvers in addition to DDIM. In our work, it is found that applying BDIA to the EDM sampling procedure produces slightly better FID score over CIFAR10.

On Accelerating Diffusion-Based Sampling Process via Improved Integration Approximation

One popular diffusion-based sampling strategy attempts to solve the reverse ordinary differential equations (ODEs) effectively. The coefficients of the obtained ODE solvers are pre-determined by the ODE formulation, the reverse discrete timesteps, and the employed ODE methods. In this paper, we consider accelerating several popular ODE-based sampling processes by optimizing certain coefficients via improved integration approximation (IIA). At each reverse timestep, we propose to minimize a mean squared error (MSE) function with respect to certain selected coefficients. The MSE is constructed by applying the original ODE solver for a set of fine-grained timesteps which in principle provides a more accurate integration approximation in predicting the next diffusion hidden state. Given a pre-trained diffusion model, the procedure for IIA for a particular number of neural functional evaluations (NFEs) only needs to be conducted once over a batch of samples. The obtained optimal solutions for those selected coefficients via minimum MSE (MMSE) can be restored and reused later on to accelerate the sampling process. Extensive experiments on EDM and DDIM show the IIA technique leads to significant performance gain when the numbers of NFEs are small.

Lookahead Diffusion Probabilistic Models for Refining Mean Estimation

We propose lookahead diffusion probabilistic models (LA-DPMs) to exploit the correlation in the outputs of the deep neural networks (DNNs) over subsequent timesteps in diffusion probabilistic models (DPMs) to refine the mean estimation of the conditional Gaussian distributions in the backward process. A typical DPM first obtains an estimate of the original data sample $\boldsymbol{x}$ by feeding the most recent state $\boldsymbol{z}_i$ and index $i$ into the DNN model and then computes the mean vector of the conditional Gaussian distribution for $\boldsymbol{z}_{i-1}$. We propose to calculate a more accurate estimate for $\boldsymbol{x}$ by performing extrapolation on the two estimates of $\boldsymbol{x}$ that are obtained by feeding $(\boldsymbol{z}_{i+1},i+1)$ and $(\boldsymbol{z}_{i},i)$ into the DNN model. The extrapolation can be easily integrated into the backward process of existing DPMs by introducing an additional connection over two consecutive timesteps, and fine-tuning is not required. Extensive experiments showed that plugging in the additional connection into DDPM, DDIM, DEIS, S-PNDM, and high-order DPM-Solvers leads to a significant performance gain in terms of FID score.

On Suppressing Range of Adaptive Stepsizes of Adam to Improve Generalisation Performance

A number of recent adaptive optimizers improve the generalisation performance of Adam by essentially reducing the variance of adaptive stepsizes to get closer to SGD with momentum. Following the above motivation, we suppress the range of the adaptive stepsizes of Adam by exploiting the layerwise gradient statistics. In particular, at each iteration, we propose to perform three consecutive operations on the second momentum v_t before using it to update a DNN model: (1): down-scaling, (2): epsilon-embedding, and (3): down-translating. The resulting algorithm is referred to as SET-Adam, where SET is a brief notation of the three operations. The down-scaling operation on v_t is performed layerwise by making use of the angles between the layerwise subvectors of v_t and the corresponding all-one subvectors. Extensive experimental results show that SET-Adam outperforms eight adaptive optimizers when training transformers and LSTMs for NLP, and VGG and ResNet for image classification over CIAF10 and CIFAR100 while matching the best performance of the eight adaptive methods when training WGAN-GP models for image generation tasks. Furthermore, SET-Adam produces higher validation accuracies than Adam and AdaBelief for training ResNet18 over ImageNet.

On Exploiting Layerwise Gradient Statistics for Effective Training of Deep Neural Networks

Adam and AdaBelief compute and make use of elementwise adaptive stepsizes in training deep neural networks (DNNs) by tracking the exponential moving average (EMA) of the squared-gradient g_t^2 and the squared prediction error (m_t-g_t)^2, respectively, where m_t is the first momentum at iteration t and can be viewed as a prediction of g_t. In this work, we attempt to find out if layerwise gradient statistics can be expoited in Adam and AdaBelief to allow for more effective training of DNNs. We address the above research question in two steps. Firstly, we slightly modify Adam and AdaBelief by introducing layerwise adaptive stepsizes in their update procedures via either pre or post processing. Empirical study indicates that the slight modification produces comparable performance for training VGG and ResNet models over CIFAR10, suggesting that layer-wise gradient statistics plays an important role towards the success of Adam and AdaBelief for at least certian DNN tasks. In the second step, instead of manual setup of layerwise stepsizes, we propose Aida, a new optimisation method, with the objective that the elementwise stepsizes within each layer have significantly small statistic variances. Motivated by the fact that (m_t-g_t)^2 in AdaBelief is conservative in comparison to g_t^2 in Adam in terms of layerwise statistic averages and variances, Aida is designed by tracking a more conservative function of m_t and g_t than (m_t-g_t)^2 in AdaBelief via layerwise orthogonal vector projections. Experimental results show that Aida produces either competitive or better performance with respect to a number of existing methods including Adam and AdaBelief for a set of challenging DNN tasks.

Extending AdamW by Leveraging Its Second Moment and Magnitude

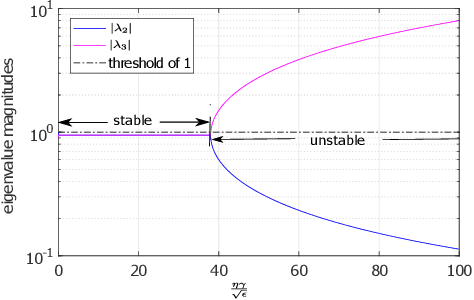
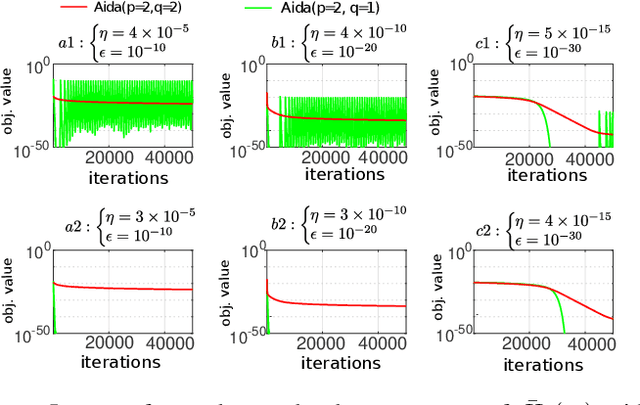
Recent work [4] analyses the local convergence of Adam in a neighbourhood of an optimal solution for a twice-differentiable function. It is found that the learning rate has to be sufficiently small to ensure local stability of the optimal solution. The above convergence results also hold for AdamW. In this work, we propose a new adaptive optimisation method by extending AdamW in two aspects with the purpose to relax the requirement on small learning rate for local stability, which we refer to as Aida. Firstly, we consider tracking the 2nd moment r_t of the pth power of the gradient-magnitudes. r_t reduces to v_t of AdamW when p=2. Suppose {m_t} is the first moment of AdamW. It is known that the update direction m_{t+1}/(v_{t+1}+epsilon)^0.5 (or m_{t+1}/(v_{t+1}^0.5+epsilon) of AdamW (or Adam) can be decomposed as the sign vector sign(m_{t+1}) multiplied elementwise by a vector of magnitudes |m_{t+1}|/(v_{t+1}+epsilon)^0.5 (or |m_{t+1}|/(v_{t+1}^0.5+epsilon)). Aida is designed to compute the qth power of the magnitude in the form of |m_{t+1}|^q/(r_{t+1}+epsilon)^(q/p) (or |m_{t+1}|^q/((r_{t+1})^(q/p)+epsilon)), which reduces to that of AdamW when (p,q)=(2,1). Suppose the origin 0 is a local optimal solution of a twice-differentiable function. It is found theoretically that when q>1 and p>1 in Aida, the origin 0 is locally stable only when the weight-decay is non-zero. Experiments are conducted for solving ten toy optimisation problems and training Transformer and Swin-Transformer for two deep learning (DL) tasks. The empirical study demonstrates that in a number of scenarios (including the two DL tasks), Aida with particular setups of (p,q) not equal to (2,1) outperforms the setup (p,q)=(2,1) of AdamW.

Coarsening Optimization for Differentiable Programming

This paper presents a novel optimization for differentiable programming named coarsening optimization. It offers a systematic way to synergize symbolic differentiation and algorithmic differentiation (AD). Through it, the granularity of the computations differentiated by each step in AD can become much larger than a single operation, and hence lead to much reduced runtime computations and data allocations in AD. To circumvent the difficulties that control flow creates to symbolic differentiation in coarsening, this work introduces phi-calculus, a novel method to allow symbolic reasoning and differentiation of computations that involve branches and loops. It further avoids "expression swell" in symbolic differentiation and balance reuse and coarsening through the design of reuse-centric segment of interest identification. Experiments on a collection of real-world applications show that coarsening optimization is effective in speeding up AD, producing several times to two orders of magnitude speedups.