On Accelerating Diffusion-Based Sampling Process via Improved Integration Approximation

One popular diffusion-based sampling strategy attempts to solve the reverse ordinary differential equations (ODEs) effectively. The coefficients of the obtained ODE solvers are pre-determined by the ODE formulation, the reverse discrete timesteps, and the employed ODE methods. In this paper, we consider accelerating several popular ODE-based sampling processes by optimizing certain coefficients via improved integration approximation (IIA). At each reverse timestep, we propose to minimize a mean squared error (MSE) function with respect to certain selected coefficients. The MSE is constructed by applying the original ODE solver for a set of fine-grained timesteps which in principle provides a more accurate integration approximation in predicting the next diffusion hidden state. Given a pre-trained diffusion model, the procedure for IIA for a particular number of neural functional evaluations (NFEs) only needs to be conducted once over a batch of samples. The obtained optimal solutions for those selected coefficients via minimum MSE (MMSE) can be restored and reused later on to accelerate the sampling process. Extensive experiments on EDM and DDIM show the IIA technique leads to significant performance gain when the numbers of NFEs are small.

Lookahead Diffusion Probabilistic Models for Refining Mean Estimation

We propose lookahead diffusion probabilistic models (LA-DPMs) to exploit the correlation in the outputs of the deep neural networks (DNNs) over subsequent timesteps in diffusion probabilistic models (DPMs) to refine the mean estimation of the conditional Gaussian distributions in the backward process. A typical DPM first obtains an estimate of the original data sample $\boldsymbol{x}$ by feeding the most recent state $\boldsymbol{z}_i$ and index $i$ into the DNN model and then computes the mean vector of the conditional Gaussian distribution for $\boldsymbol{z}_{i-1}$. We propose to calculate a more accurate estimate for $\boldsymbol{x}$ by performing extrapolation on the two estimates of $\boldsymbol{x}$ that are obtained by feeding $(\boldsymbol{z}_{i+1},i+1)$ and $(\boldsymbol{z}_{i},i)$ into the DNN model. The extrapolation can be easily integrated into the backward process of existing DPMs by introducing an additional connection over two consecutive timesteps, and fine-tuning is not required. Extensive experiments showed that plugging in the additional connection into DDPM, DDIM, DEIS, S-PNDM, and high-order DPM-Solvers leads to a significant performance gain in terms of FID score.

Extending AdamW by Leveraging Its Second Moment and Magnitude

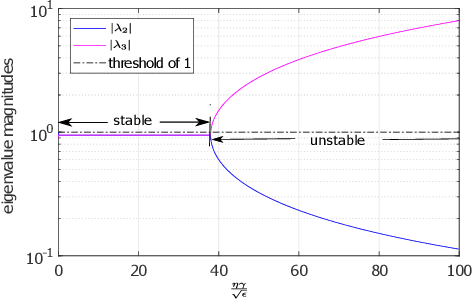
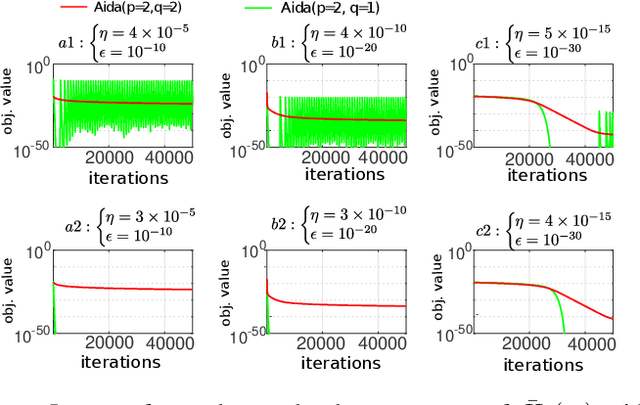
Recent work [4] analyses the local convergence of Adam in a neighbourhood of an optimal solution for a twice-differentiable function. It is found that the learning rate has to be sufficiently small to ensure local stability of the optimal solution. The above convergence results also hold for AdamW. In this work, we propose a new adaptive optimisation method by extending AdamW in two aspects with the purpose to relax the requirement on small learning rate for local stability, which we refer to as Aida. Firstly, we consider tracking the 2nd moment r_t of the pth power of the gradient-magnitudes. r_t reduces to v_t of AdamW when p=2. Suppose {m_t} is the first moment of AdamW. It is known that the update direction m_{t+1}/(v_{t+1}+epsilon)^0.5 (or m_{t+1}/(v_{t+1}^0.5+epsilon) of AdamW (or Adam) can be decomposed as the sign vector sign(m_{t+1}) multiplied elementwise by a vector of magnitudes |m_{t+1}|/(v_{t+1}+epsilon)^0.5 (or |m_{t+1}|/(v_{t+1}^0.5+epsilon)). Aida is designed to compute the qth power of the magnitude in the form of |m_{t+1}|^q/(r_{t+1}+epsilon)^(q/p) (or |m_{t+1}|^q/((r_{t+1})^(q/p)+epsilon)), which reduces to that of AdamW when (p,q)=(2,1). Suppose the origin 0 is a local optimal solution of a twice-differentiable function. It is found theoretically that when q>1 and p>1 in Aida, the origin 0 is locally stable only when the weight-decay is non-zero. Experiments are conducted for solving ten toy optimisation problems and training Transformer and Swin-Transformer for two deep learning (DL) tasks. The empirical study demonstrates that in a number of scenarios (including the two DL tasks), Aida with particular setups of (p,q) not equal to (2,1) outperforms the setup (p,q)=(2,1) of AdamW.