On Exact Bit-level Reversible Transformers Without Changing Architectures

In the literature, various reversible deep neural networks (DNN) models have been proposed to reduce memory consumption or improve data-throughput in the training process. However, almost all existing reversible DNNs either are constrained to have special structures or are constructed by modifying the original DNN architectures considerably to enable reversibility. In this work, we propose exact bit-level reversible transformers without changing the architectures in the inference procedure. The basic idea is to first treat each transformer block as the Euler integration approximation for solving an ordinary differential equation (ODE) and then incorporate the technique of bidirectional integration approximation (BDIA) (see [26]) for BDIA-based diffusion inversion) into the neural architecture together with activation quantization to make it exactly bit-level reversible, referred to as BDIA-transformer. In the training process, we let a hyper-parameter $\gamma$ in BDIA-transformer randomly take one of the two values $\{0.5, -0.5\}$ per transformer block for averaging two consecutive integration approximations, which regularizes the models for improving the validation accuracy. Light-weight side information per transformer block is required to be stored in the forward process to account for binary quantization loss to enable exact bit-level reversibility. In the inference procedure, the expectation $\mathbb{E}(\gamma)=0$ is taken to make the resulting architectures of BDIA-transformer be identical to transformers up to activation quantization. Empirical study indicates that BDIA-transformers outperform their original counterparts notably due to the regularization effect of the $\gamma$ parameter.

Variance Constrained Autoencoding

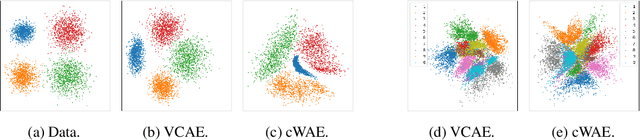
Recent state-of-the-art autoencoder based generative models have an encoder-decoder structure and learn a latent representation with a pre-defined distribution that can be sampled from. Implementing the encoder networks of these models in a stochastic manner provides a natural and common approach to avoid overfitting and enforce a smooth decoder function. However, we show that for stochastic encoders, simultaneously attempting to enforce a distribution constraint and minimising an output distortion leads to a reduction in generative and reconstruction quality. In addition, attempting to enforce a latent distribution constraint is not reasonable when performing disentanglement. Hence, we propose the variance-constrained autoencoder (VCAE), which only enforces a variance constraint on the latent distribution. Our experiments show that VCAE improves upon Wasserstein Autoencoder and the Variational Autoencoder in both reconstruction and generative quality on MNIST and CelebA. Moreover, we show that VCAE equipped with a total correlation penalty term performs equivalently to FactorVAE at learning disentangled representations on 3D-Shapes while being a more principled approach.

Approximated Orthonormal Normalisation in Training Neural Networks

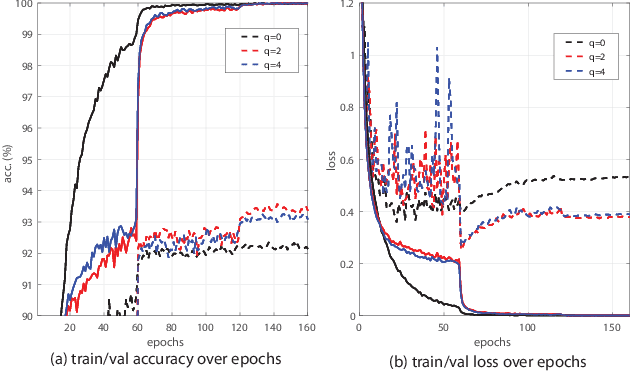
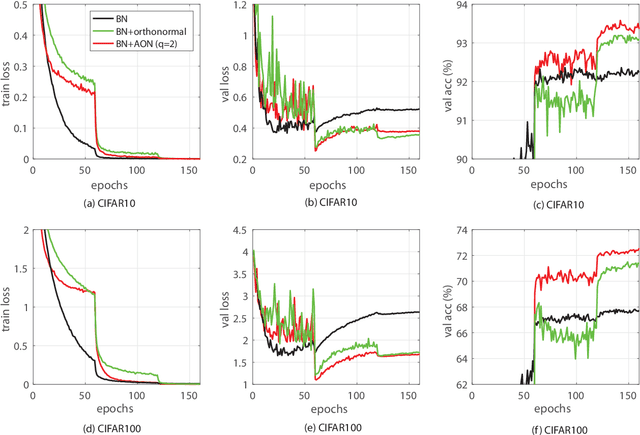
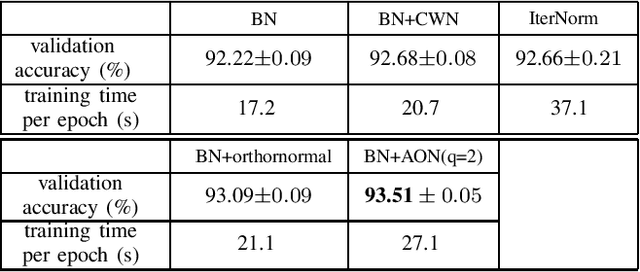
Generalisation of a deep neural network (DNN) is one major concern when employing the deep learning approach for solving practical problems. In this paper we propose a new technique, named approximated orthonormal normalisation (AON), to improve the generalisation capacity of a DNN model. Considering a weight matrix W from a particular neural layer in the model, our objective is to design a function h(W) such that its row vectors are approximately orthogonal to each other while allowing the DNN model to fit the training data sufficiently accurate. By doing so, it would avoid co-adaptation among neurons of the same layer to be able to improve network-generalisation capacity. Specifically, at each iteration, we first approximate (WW^T)^(-1/2) using its Taylor expansion before multiplying the matrix W. After that, the matrix product is then normalised by applying the spectral normalisation (SN) technique to obtain h(W). Conceptually speaking, AON is designed to turn orthonormal regularisation into orthonormal normalisation to avoid manual balancing the original and penalty functions. Experimental results show that AON yields promising validation performance compared to orthonormal regularisation.

Bounded Information Rate Variational Autoencoders

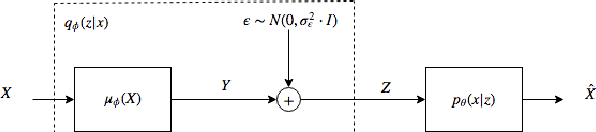
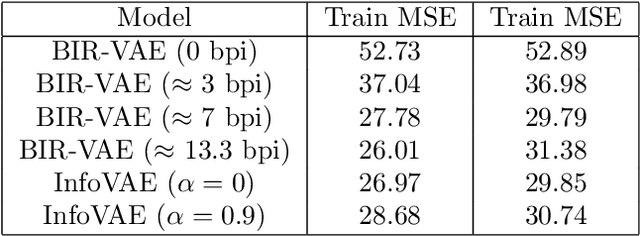
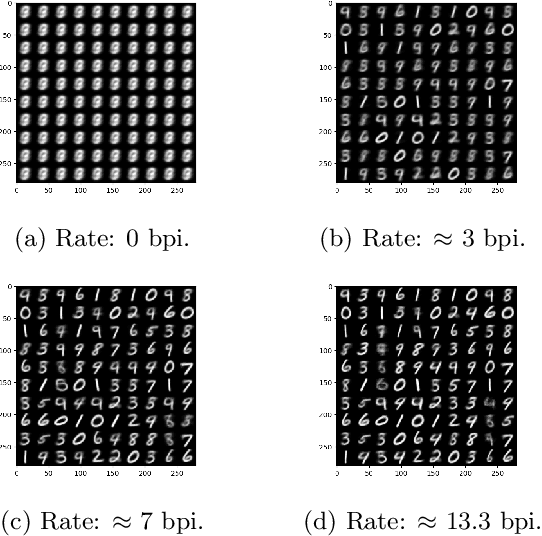
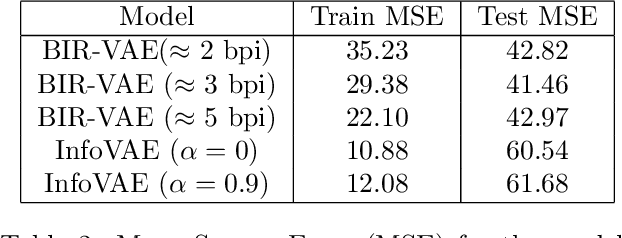
This paper introduces a new member of the family of Variational Autoencoders (VAE) that constrains the rate of information transferred by the latent layer. The latent layer is interpreted as a communication channel, the information rate of which is bound by imposing a pre-set signal-to-noise ratio. The new constraint subsumes the mutual information between the input and latent variables, combining naturally with the likelihood objective of the observed data as used in a conventional VAE. The resulting Bounded-Information-Rate Variational Autoencoder (BIR-VAE) provides a meaningful latent representation with an information resolution that can be specified directly in bits by the system designer. The rate constraint can be used to prevent overtraining, and the method naturally facilitates quantisation of the latent variables at the set rate. Our experiments confirm that the BIR-VAE has a meaningful latent representation and that its performance is at least as good as state-of-the-art competing algorithms, but with lower computational complexity.