Truncated Non-Uniform Quantization for Distributed SGD

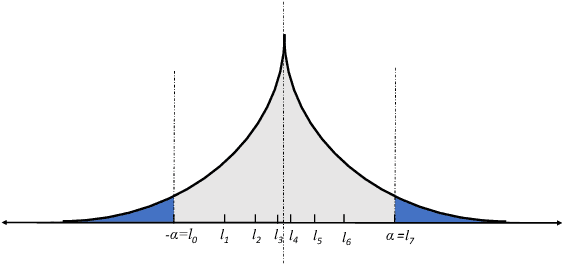
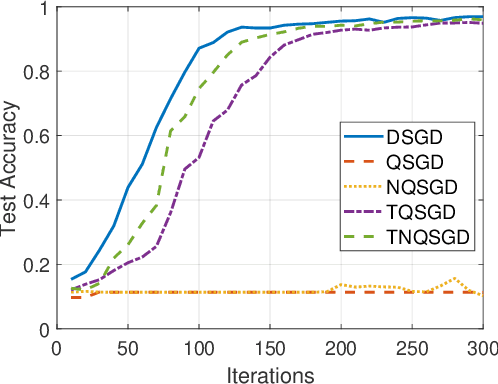
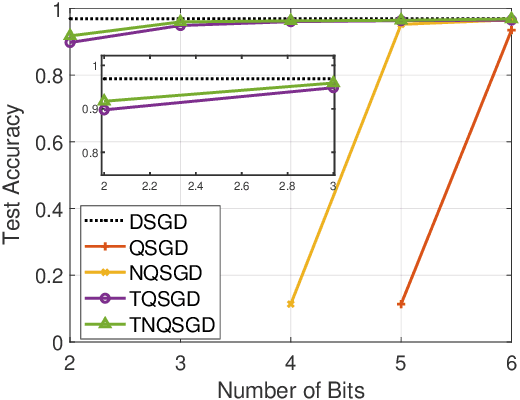
To address the communication bottleneck challenge in distributed learning, our work introduces a novel two-stage quantization strategy designed to enhance the communication efficiency of distributed Stochastic Gradient Descent (SGD). The proposed method initially employs truncation to mitigate the impact of long-tail noise, followed by a non-uniform quantization of the post-truncation gradients based on their statistical characteristics. We provide a comprehensive convergence analysis of the quantized distributed SGD, establishing theoretical guarantees for its performance. Furthermore, by minimizing the convergence error, we derive optimal closed-form solutions for the truncation threshold and non-uniform quantization levels under given communication constraints. Both theoretical insights and extensive experimental evaluations demonstrate that our proposed algorithm outperforms existing quantization schemes, striking a superior balance between communication efficiency and convergence performance.

Improved Quantization Strategies for Managing Heavy-tailed Gradients in Distributed Learning

Gradient compression has surfaced as a key technique to address the challenge of communication efficiency in distributed learning. In distributed deep learning, however, it is observed that gradient distributions are heavy-tailed, with outliers significantly influencing the design of compression strategies. Existing parameter quantization methods experience performance degradation when this heavy-tailed feature is ignored. In this paper, we introduce a novel compression scheme specifically engineered for heavy-tailed gradients, which effectively combines gradient truncation with quantization. This scheme is adeptly implemented within a communication-limited distributed Stochastic Gradient Descent (SGD) framework. We consider a general family of heavy-tail gradients that follow a power-law distribution, we aim to minimize the error resulting from quantization, thereby determining optimal values for two critical parameters: the truncation threshold and the quantization density. We provide a theoretical analysis on the convergence error bound under both uniform and non-uniform quantization scenarios. Comparative experiments with other benchmarks demonstrate the effectiveness of our proposed method in managing the heavy-tailed gradients in a distributed learning environment.

Killing Two Birds with One Stone: Quantization Achieves Privacy in Distributed Learning

Communication efficiency and privacy protection are two critical issues in distributed machine learning. Existing methods tackle these two issues separately and may have a high implementation complexity that constrains their application in a resource-limited environment. We propose a comprehensive quantization-based solution that could simultaneously achieve communication efficiency and privacy protection, providing new insights into the correlated nature of communication and privacy. Specifically, we demonstrate the effectiveness of our proposed solutions in the distributed stochastic gradient descent (SGD) framework by adding binomial noise to the uniformly quantized gradients to reach the desired differential privacy level but with a minor sacrifice in communication efficiency. We theoretically capture the new trade-offs between communication, privacy, and learning performance.

Adaptive Top-K in SGD for Communication-Efficient Distributed Learning

Distributed stochastic gradient descent (SGD) with gradient compression has emerged as a communication-efficient solution to accelerate distributed learning. Top-K sparsification is one of the most popular gradient compression methods that sparsifies the gradient in a fixed degree during model training. However, there lacks an approach to adaptively adjust the degree of sparsification to maximize the potential of model performance or training speed. This paper addresses this issue by proposing a novel adaptive Top-K SGD framework, enabling adaptive degree of sparsification for each gradient descent step to maximize the convergence performance by exploring the trade-off between communication cost and convergence error. Firstly, we derive an upper bound of the convergence error for the adaptive sparsification scheme and the loss function. Secondly, we design the algorithm by minimizing the convergence error under the communication cost constraints. Finally, numerical results show that the proposed adaptive Top-K in SGD achieves a significantly better convergence rate compared with the state-of-the-art methods.

DQ-SGD: Dynamic Quantization in SGD for Communication-Efficient Distributed Learning

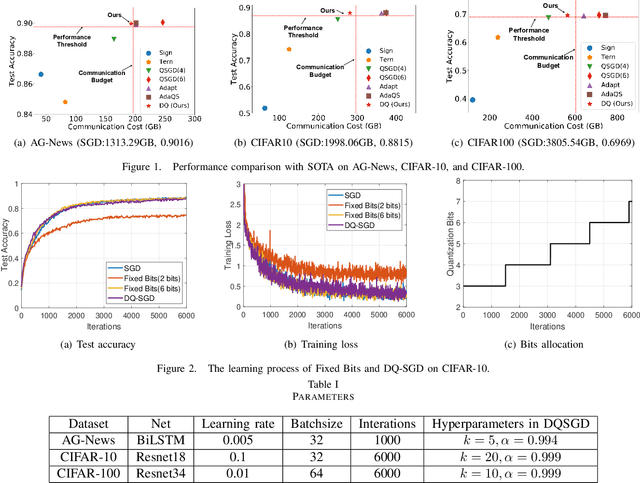
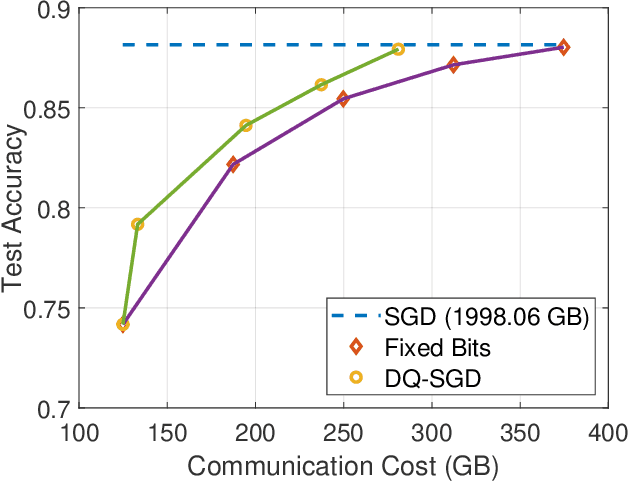
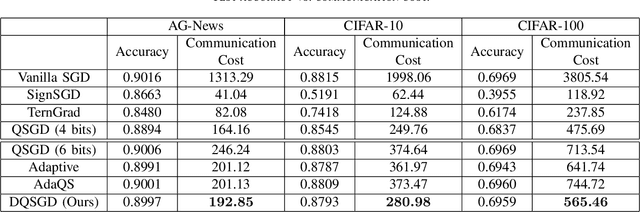
Gradient quantization is an emerging technique in reducing communication costs in distributed learning. Existing gradient quantization algorithms often rely on engineering heuristics or empirical observations, lacking a systematic approach to dynamically quantize gradients. This paper addresses this issue by proposing a novel dynamically quantized SGD (DQ-SGD) framework, enabling us to dynamically adjust the quantization scheme for each gradient descent step by exploring the trade-off between communication cost and convergence error. We derive an upper bound, tight in some cases, of the convergence error for a restricted family of quantization schemes and loss functions. We design our DQ-SGD algorithm via minimizing the communication cost under the convergence error constraints. Finally, through extensive experiments on large-scale natural language processing and computer vision tasks on AG-News, CIFAR-10, and CIFAR-100 datasets, we demonstrate that our quantization scheme achieves better tradeoffs between the communication cost and learning performance than other state-of-the-art gradient quantization methods.