Online Learning of Deceptive Policies under Intermittent Observation

In supervisory control settings, autonomous systems are not monitored continuously. Instead, monitoring often occurs at sporadic intervals within known bounds. We study the problem of deception, where an agent pursues a private objective while remaining plausibly compliant with a supervisor's reference policy when observations occur. Motivated by the behavior of real, human supervisors, we situate the problem within Theory of Mind: the representation of what an observer believes and expects to see. We show that Theory of Mind can be repurposed to steer online reinforcement learning (RL) toward such deceptive behavior. We model the supervisor's expectations and distill from them a single, calibrated scalar -- the expected evidence of deviation if an observation were to happen now. This scalar combines how unlike the reference and current action distributions appear, with the agent's belief that an observation is imminent. Injected as a state-dependent weight into a KL-regularized policy improvement step within an online RL loop, this scalar informs a closed-form update that smoothly trades off self-interest and compliance, thus sidestepping hand-crafted or heuristic policies. In real-world, real-time hardware experiments on marine (ASV) and aerial (UAV) navigation, our ToM-guided RL runs online, achieves high return and success with observed-trace evidence calibrated to the supervisor's expectations.

Motion Planning and Control with Unknown Nonlinear Dynamics through Predicted Reachability

Autonomous motion planning under unknown nonlinear dynamics presents significant challenges. An agent needs to continuously explore the system dynamics to acquire its properties, such as reachability, in order to guide system navigation adaptively. In this paper, we propose a hybrid planning-control framework designed to compute a feasible trajectory toward a target. Our approach involves partitioning the state space and approximating the system by a piecewise affine (PWA) system with constrained control inputs. By abstracting the PWA system into a directed weighted graph, we incrementally update the existence of its edges via affine system identification and reach control theory, introducing a predictive reachability condition by exploiting prior information of the unknown dynamics. Heuristic weights are assigned to edges based on whether their existence is certain or remains indeterminate. Consequently, we propose a framework that adaptively collects and analyzes data during mission execution, continually updates the predictive graph, and synthesizes a controller online based on the graph search outcomes. We demonstrate the efficacy of our approach through simulation scenarios involving a mobile robot operating in unknown terrains, with its unknown dynamics abstracted as a single integrator model.

TAB-Fields: A Maximum Entropy Framework for Mission-Aware Adversarial Planning

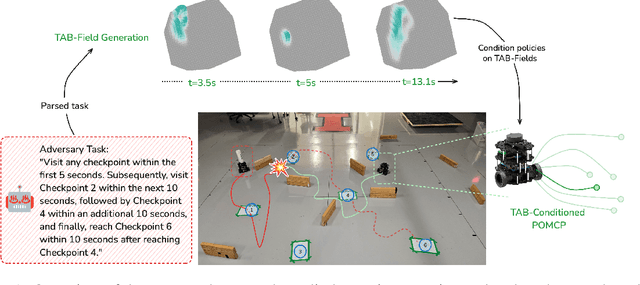
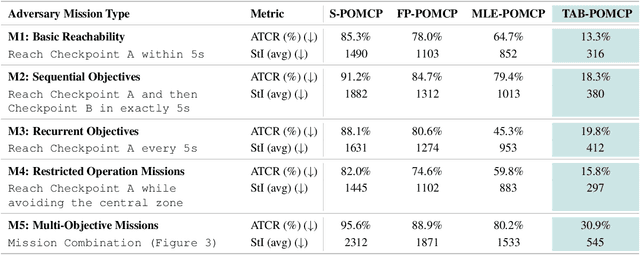
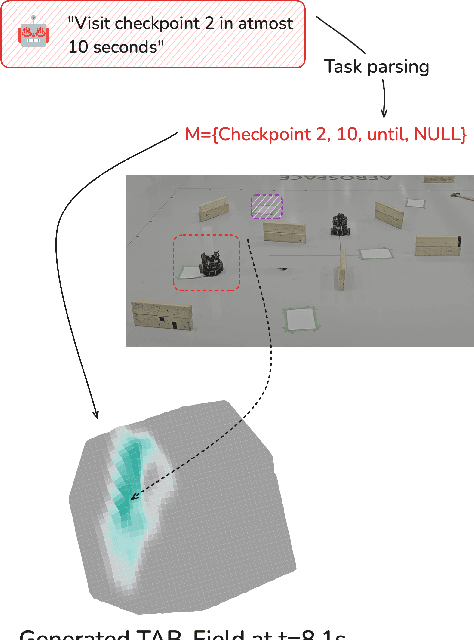
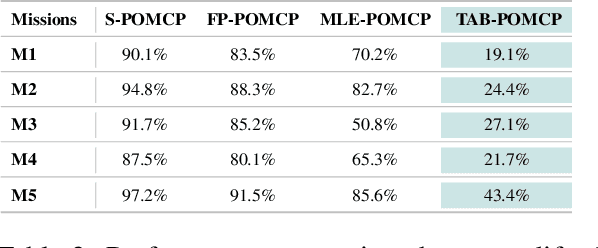
Autonomous agents operating in adversarial scenarios face a fundamental challenge: while they may know their adversaries' high-level objectives, such as reaching specific destinations within time constraints, the exact policies these adversaries will employ remain unknown. Traditional approaches address this challenge by treating the adversary's state as a partially observable element, leading to a formulation as a Partially Observable Markov Decision Process (POMDP). However, the induced belief-space dynamics in a POMDP require knowledge of the system's transition dynamics, which, in this case, depend on the adversary's unknown policy. Our key observation is that while an adversary's exact policy is unknown, their behavior is necessarily constrained by their mission objectives and the physical environment, allowing us to characterize the space of possible behaviors without assuming specific policies. In this paper, we develop Task-Aware Behavior Fields (TAB-Fields), a representation that captures adversary state distributions over time by computing the most unbiased probability distribution consistent with known constraints. We construct TAB-Fields by solving a constrained optimization problem that minimizes additional assumptions about adversary behavior beyond mission and environmental requirements. We integrate TAB-Fields with standard planning algorithms by introducing TAB-conditioned POMCP, an adaptation of Partially Observable Monte Carlo Planning. Through experiments in simulation with underwater robots and hardware implementations with ground robots, we demonstrate that our approach achieves superior performance compared to baselines that either assume specific adversary policies or neglect mission constraints altogether. Evaluation videos and code are available at https://tab-fields.github.io.

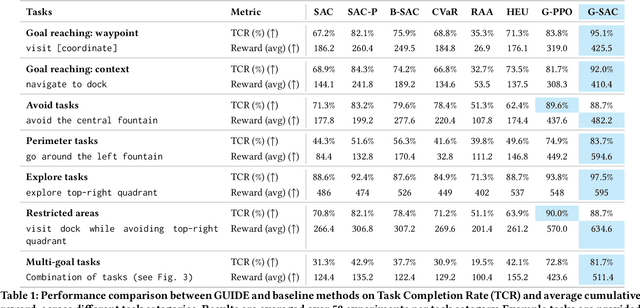
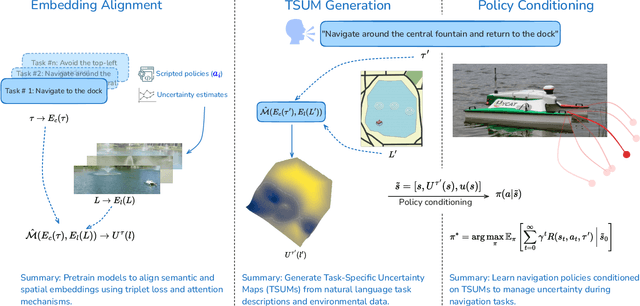
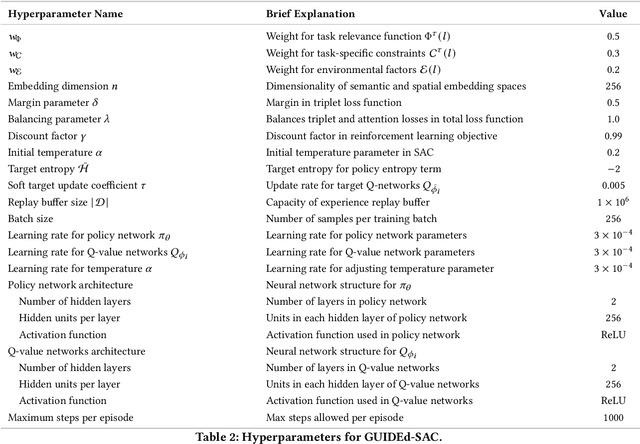
Enhancing Robot Navigation Policies with Task-Specific Uncertainty Management

Robots performing navigation tasks in complex environments face significant challenges due to uncertainty in state estimation. Effectively managing this uncertainty is crucial, but the optimal approach varies depending on the specific details of the task: different tasks require varying levels of precision in different regions of the environment. For instance, a robot navigating a crowded space might need precise localization near obstacles but can operate effectively with less precise state estimates in open areas. This varying need for certainty in different parts of the environment, depending on the task, calls for policies that can adapt their uncertainty management strategies based on task-specific requirements. In this paper, we present a framework for integrating task-specific uncertainty requirements directly into navigation policies. We introduce Task-Specific Uncertainty Map (TSUM), which represents acceptable levels of state estimation uncertainty across different regions of the operating environment for a given task. Using TSUM, we propose Generalized Uncertainty Integration for Decision-Making and Execution (GUIDE), a policy conditioning framework that incorporates these uncertainty requirements into the robot's decision-making process. We find that conditioning policies on TSUMs provides an effective way to express task-specific uncertainty requirements and enables the robot to reason about the context-dependent value of certainty. We show how integrating GUIDE into reinforcement learning frameworks allows the agent to learn navigation policies without the need for explicit reward engineering to balance task completion and uncertainty management. We evaluate GUIDE on a variety of real-world navigation tasks and find that it demonstrates significant improvements in task completion rates compared to baselines. Evaluation videos can be found at https://guided-agents.github.io.

ComTraQ-MPC: Meta-Trained DQN-MPC Integration for Trajectory Tracking with Limited Active Localization Updates

Optimal decision-making for trajectory tracking in partially observable, stochastic environments where the number of active localization updates -- the process by which the agent obtains its true state information from the sensors -- are limited, presents a significant challenge. Traditional methods often struggle to balance resource conservation, accurate state estimation and precise tracking, resulting in suboptimal performance. This problem is particularly pronounced in environments with large action spaces, where the need for frequent, accurate state data is paramount, yet the capacity for active localization updates is restricted by external limitations. This paper introduces ComTraQ-MPC, a novel framework that combines Deep Q-Networks (DQN) and Model Predictive Control (MPC) to optimize trajectory tracking with constrained active localization updates. The meta-trained DQN ensures adaptive active localization scheduling, while the MPC leverages available state information to improve tracking. The central contribution of this work is their reciprocal interaction: DQN's update decisions inform MPC's control strategy, and MPC's outcomes refine DQN's learning, creating a cohesive, adaptive system. Empirical evaluations in simulated and real-world settings demonstrate that ComTraQ-MPC significantly enhances operational efficiency and accuracy, providing a generalizable and approximately optimal solution for trajectory tracking in complex partially observable environments.

Weathering Ongoing Uncertainty: Learning and Planning in a Time-Varying Partially Observable Environment

Optimal decision-making presents a significant challenge for autonomous systems operating in uncertain, stochastic and time-varying environments. Environmental variability over time can significantly impact the system's optimal decision making strategy for mission completion. To model such environments, our work combines the previous notion of Time-Varying Markov Decision Processes (TVMDP) with partial observability and introduces Time-Varying Partially Observable Markov Decision Processes (TV-POMDP). We propose a two-pronged approach to accurately estimate and plan within the TV-POMDP: 1) Memory Prioritized State Estimation (MPSE), which leverages weighted memory to provide more accurate time-varying transition estimates; and 2) an MPSE-integrated planning strategy that optimizes long-term rewards while accounting for temporal constraint. We validate the proposed framework and algorithms using simulations and hardware, with robots exploring a partially observable, time-varying environments. Our results demonstrate superior performance over standard methods, highlighting the framework's effectiveness in stochastic, uncertain, time-varying domains.