Capacity-Aware Planning and Scheduling in Budget-Constrained Monotonic MDPs: A Meta-RL Approach

Many real-world sequential repair problems can be effectively modeled using monotonic Markov Decision Processes (MDPs), where the system state stochastically decreases and can only be increased by performing a restorative action. This work addresses the problem of solving multi-component monotonic MDPs with both budget and capacity constraints. The budget constraint limits the total number of restorative actions and the capacity constraint limits the number of restorative actions that can be performed simultaneously. While prior methods dealt with budget constraints, including capacity constraints in prior methods leads to an exponential increase in computational complexity as the number of components in the MDP grows. We propose a two-step planning approach to address this challenge. First, we partition the components of the multi-component MDP into groups, where the number of groups is determined by the capacity constraint. We achieve this partitioning by solving a Linear Sum Assignment Problem (LSAP). Each group is then allocated a fraction of the total budget proportional to its size. This partitioning effectively decouples the large multi-component MDP into smaller subproblems, which are computationally feasible because the capacity constraint is simplified and the budget constraint can be addressed using existing methods. Subsequently, we use a meta-trained PPO agent to obtain an approximately optimal policy for each group. To validate our approach, we apply it to the problem of scheduling repairs for a large group of industrial robots, constrained by a limited number of repair technicians and a total repair budget. Our results demonstrate that the proposed method outperforms baseline approaches in terms of maximizing the average uptime of the robot swarm, particularly for large swarm sizes.

Solving Truly Massive Budgeted Monotonic POMDPs with Oracle-Guided Meta-Reinforcement Learning

Monotonic Partially Observable Markov Decision Processes (POMDPs), where the system state progressively decreases until a restorative action is performed, can be used to model sequential repair problems effectively. This paper considers the problem of solving budget-constrained multi-component monotonic POMDPs, where a finite budget limits the maximal number of restorative actions. For a large number of components, solving such a POMDP using current methods is computationally intractable due to the exponential growth in the state space with an increasing number of components. To address this challenge, we propose a two-step approach. Since the individual components of a budget-constrained multi-component monotonic POMDP are only connected via the shared budget, we first approximate the optimal budget allocation among these components using an approximation of each component POMDP's optimal value function which is obtained through a random forest model. Subsequently, we introduce an oracle-guided meta-trained Proximal Policy Optimization (PPO) algorithm to solve each of the independent budget-constrained single-component monotonic POMDPs. The oracle policy is obtained by performing value iteration on the corresponding monotonic Markov Decision Process (MDP). This two-step method provides scalability in solving truly massive multi-component monotonic POMDPs. To demonstrate the efficacy of our approach, we consider a real-world maintenance scenario that involves inspection and repair of an administrative building by a team of agents within a maintenance budget. Finally, we perform a computational complexity analysis for a varying number of components to show the scalability of the proposed approach.

ComTraQ-MPC: Meta-Trained DQN-MPC Integration for Trajectory Tracking with Limited Active Localization Updates

Optimal decision-making for trajectory tracking in partially observable, stochastic environments where the number of active localization updates -- the process by which the agent obtains its true state information from the sensors -- are limited, presents a significant challenge. Traditional methods often struggle to balance resource conservation, accurate state estimation and precise tracking, resulting in suboptimal performance. This problem is particularly pronounced in environments with large action spaces, where the need for frequent, accurate state data is paramount, yet the capacity for active localization updates is restricted by external limitations. This paper introduces ComTraQ-MPC, a novel framework that combines Deep Q-Networks (DQN) and Model Predictive Control (MPC) to optimize trajectory tracking with constrained active localization updates. The meta-trained DQN ensures adaptive active localization scheduling, while the MPC leverages available state information to improve tracking. The central contribution of this work is their reciprocal interaction: DQN's update decisions inform MPC's control strategy, and MPC's outcomes refine DQN's learning, creating a cohesive, adaptive system. Empirical evaluations in simulated and real-world settings demonstrate that ComTraQ-MPC significantly enhances operational efficiency and accuracy, providing a generalizable and approximately optimal solution for trajectory tracking in complex partially observable environments.

Welfare Maximization Algorithm for Solving Budget-Constrained Multi-Component POMDPs

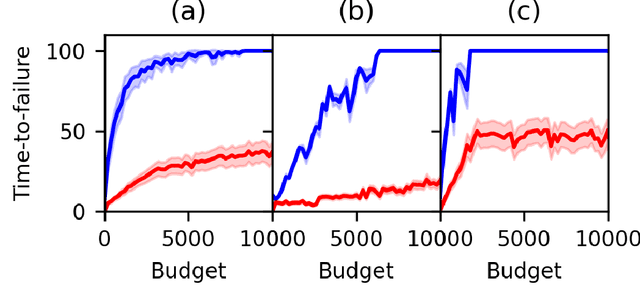
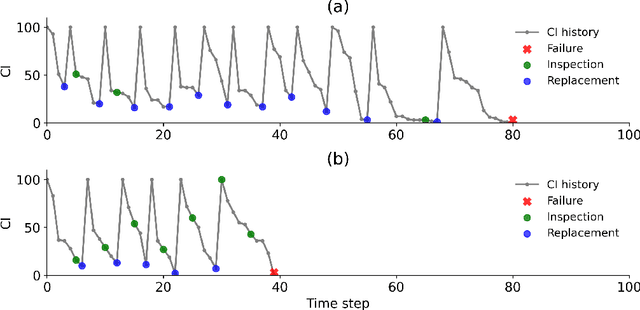
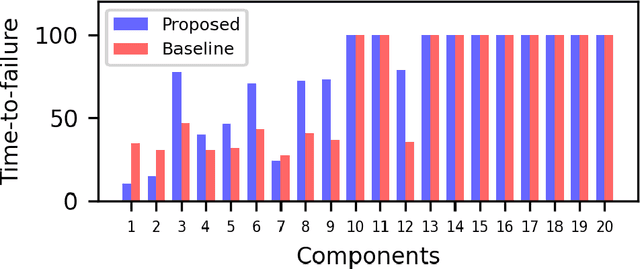
Partially Observable Markov Decision Processes (POMDPs) provide an efficient way to model real-world sequential decision making processes. Motivated by the problem of maintenance and inspection of a group of infrastructure components with independent dynamics, this paper presents an algorithm to find the optimal policy for a multi-component budget-constrained POMDP. We first introduce a budgeted-POMDP model (b-POMDP) which enables us to find the optimal policy for a POMDP while adhering to budget constraints. Next, we prove that the value function or maximal collected reward for a b-POMDP is a concave function of the budget for the finite horizon case. Our second contribution is an algorithm to calculate the optimal policy for a multi-component budget-constrained POMDP by finding the optimal budget split among the individual component POMDPs. The optimal budget split is posed as a welfare maximization problem and the solution is computed by exploiting the concave nature of the value function. We illustrate the effectiveness of the proposed algorithm by proposing a maintenance and inspection policy for a group of real-world infrastructure components with different deterioration dynamics, inspection and maintenance costs. We show that the proposed algorithm vastly outperforms the policy currently used in practice.