Welfare Maximization Algorithm for Solving Budget-Constrained Multi-Component POMDPs

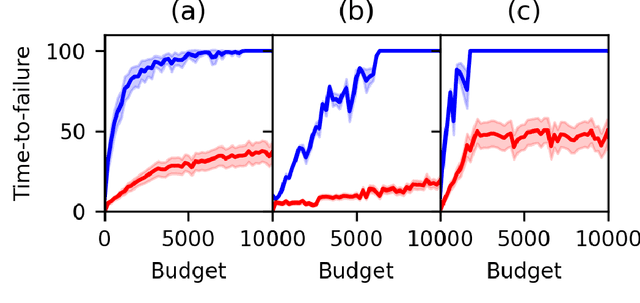
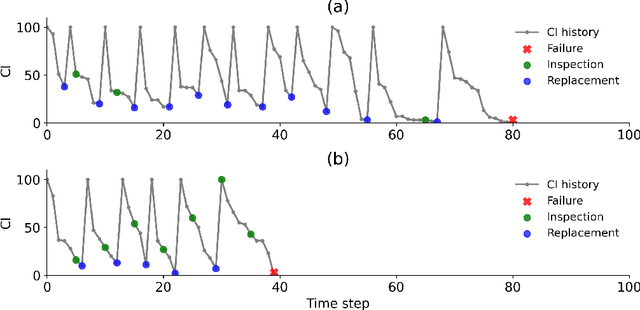
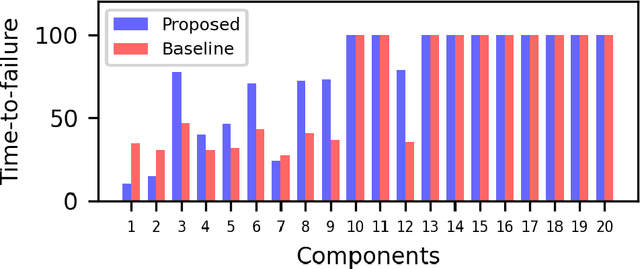
Partially Observable Markov Decision Processes (POMDPs) provide an efficient way to model real-world sequential decision making processes. Motivated by the problem of maintenance and inspection of a group of infrastructure components with independent dynamics, this paper presents an algorithm to find the optimal policy for a multi-component budget-constrained POMDP. We first introduce a budgeted-POMDP model (b-POMDP) which enables us to find the optimal policy for a POMDP while adhering to budget constraints. Next, we prove that the value function or maximal collected reward for a b-POMDP is a concave function of the budget for the finite horizon case. Our second contribution is an algorithm to calculate the optimal policy for a multi-component budget-constrained POMDP by finding the optimal budget split among the individual component POMDPs. The optimal budget split is posed as a welfare maximization problem and the solution is computed by exploiting the concave nature of the value function. We illustrate the effectiveness of the proposed algorithm by proposing a maintenance and inspection policy for a group of real-world infrastructure components with different deterioration dynamics, inspection and maintenance costs. We show that the proposed algorithm vastly outperforms the policy currently used in practice.