InfraLib: Enabling Reinforcement Learning and Decision Making for Large Scale Infrastructure Management

Efficient management of infrastructure systems is crucial for economic stability, sustainability, and public safety. However, infrastructure management is challenging due to the vast scale of systems, stochastic deterioration of components, partial observability, and resource constraints. While data-driven approaches like reinforcement learning (RL) offer a promising avenue for optimizing management policies, their application to infrastructure has been limited by the lack of suitable simulation environments. We introduce InfraLib, a comprehensive framework for modeling and analyzing infrastructure management problems. InfraLib employs a hierarchical, stochastic approach to realistically model infrastructure systems and their deterioration. It supports practical functionality such as modeling component unavailability, cyclical budgets, and catastrophic failures. To facilitate research, InfraLib provides tools for expert data collection, simulation-driven analysis, and visualization. We demonstrate InfraLib's capabilities through case studies on a real-world road network and a synthetic benchmark with 100,000 components.

Welfare Maximization Algorithm for Solving Budget-Constrained Multi-Component POMDPs

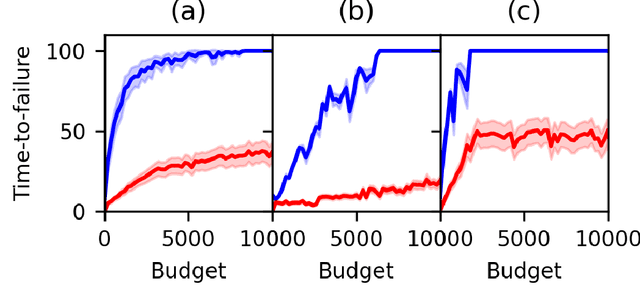
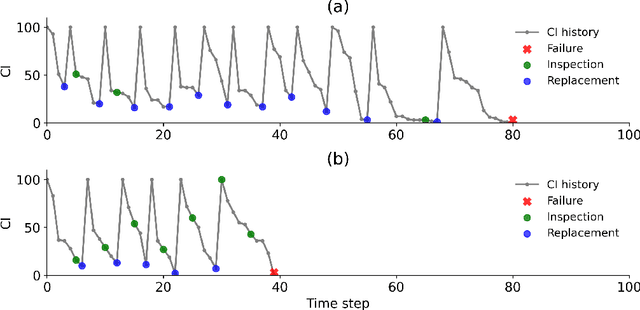
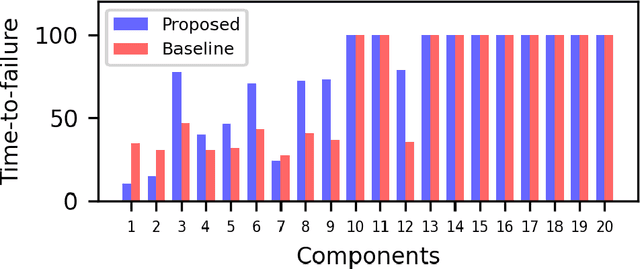
Partially Observable Markov Decision Processes (POMDPs) provide an efficient way to model real-world sequential decision making processes. Motivated by the problem of maintenance and inspection of a group of infrastructure components with independent dynamics, this paper presents an algorithm to find the optimal policy for a multi-component budget-constrained POMDP. We first introduce a budgeted-POMDP model (b-POMDP) which enables us to find the optimal policy for a POMDP while adhering to budget constraints. Next, we prove that the value function or maximal collected reward for a b-POMDP is a concave function of the budget for the finite horizon case. Our second contribution is an algorithm to calculate the optimal policy for a multi-component budget-constrained POMDP by finding the optimal budget split among the individual component POMDPs. The optimal budget split is posed as a welfare maximization problem and the solution is computed by exploiting the concave nature of the value function. We illustrate the effectiveness of the proposed algorithm by proposing a maintenance and inspection policy for a group of real-world infrastructure components with different deterioration dynamics, inspection and maintenance costs. We show that the proposed algorithm vastly outperforms the policy currently used in practice.