On the Factory Floor: ML Engineering for Industrial-Scale Ads Recommendation Models

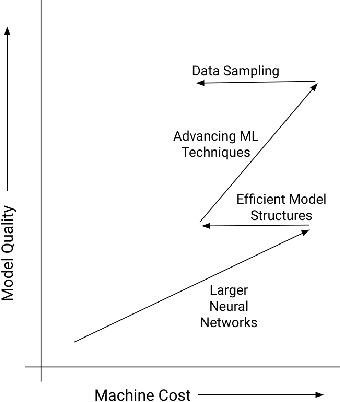
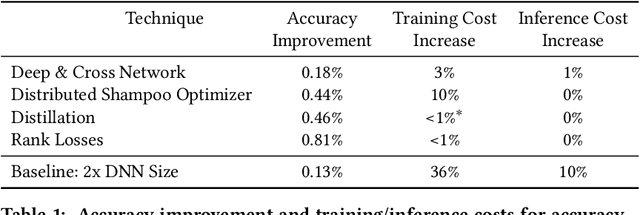
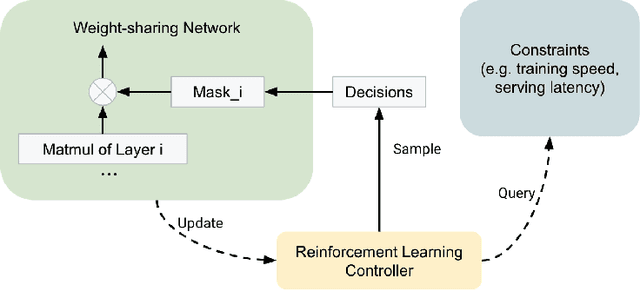
For industrial-scale advertising systems, prediction of ad click-through rate (CTR) is a central problem. Ad clicks constitute a significant class of user engagements and are often used as the primary signal for the usefulness of ads to users. Additionally, in cost-per-click advertising systems where advertisers are charged per click, click rate expectations feed directly into value estimation. Accordingly, CTR model development is a significant investment for most Internet advertising companies. Engineering for such problems requires many machine learning (ML) techniques suited to online learning that go well beyond traditional accuracy improvements, especially concerning efficiency, reproducibility, calibration, credit attribution. We present a case study of practical techniques deployed in Google's search ads CTR model. This paper provides an industry case study highlighting important areas of current ML research and illustrating how impactful new ML methods are evaluated and made useful in a large-scale industrial setting.

Real World Large Scale Recommendation Systems Reproducibility and Smooth Activations

Real world recommendation systems influence a constantly growing set of domains. With deep networks, that now drive such systems, recommendations have been more relevant to the user's interests and tasks. However, they may not always be reproducible even if produced by the same system for the same user, recommendation sequence, request, or query. This problem received almost no attention in academic publications, but is, in fact, very realistic and critical in real production systems. We consider reproducibility of real large scale deep models, whose predictions determine such recommendations. We demonstrate that the celebrated Rectified Linear Unit (ReLU) activation, used in deep models, can be a major contributor to irreproducibility. We propose the use of smooth activations to improve recommendation reproducibility. We describe a novel family of smooth activations; Smooth ReLU (SmeLU), designed to improve reproducibility with mathematical simplicity, with potentially cheaper implementation. SmeLU is a member of a wider family of smooth activations. While other techniques that improve reproducibility in real systems usually come at accuracy costs, smooth activations not only improve reproducibility, but can even give accuracy gains. We report metrics from real systems in which we were able to productionalize SmeLU with substantial reproducibility gains and better accuracy-reproducibility trade-offs. These include click-through-rate (CTR) prediction systems, content, and application recommendation systems.

Reproducibility in Optimization: Theoretical Framework and Limits

We initiate a formal study of reproducibility in optimization. We define a quantitative measure of reproducibility of optimization procedures in the face of noisy or error-prone operations such as inexact or stochastic gradient computations or inexact initialization. We then analyze several convex optimization settings of interest such as smooth, non-smooth, and strongly-convex objective functions and establish tight bounds on the limits of reproducibility in each setting. Our analysis reveals a fundamental trade-off between computation and reproducibility: more computation is necessary (and sufficient) for better reproducibility.

Synthesizing Irreproducibility in Deep Networks

The success and superior performance of deep networks is spreading their popularity and use to an increasing number of applications. Very recent works, however, demonstrate that modern day deep networks suffer from irreproducibility (also referred to as nondeterminism or underspecification). Two or more models that are identical in architecture, structure, training hyper-parameters, and parameters, and that are trained on exactly the same training data, yield different predictions on individual previously unseen examples. Thus, a model that performs well on controlled test data, may perform in unexpected ways when deployed in the real world, whose data is expected to be similar to the test data. We study simple synthetic models and data to understand the origins of these problems. We show that even with a single nonlinearity and for very simple data and models, irreproducibility occurs. Our study demonstrates the effects of randomness in initialization, training data shuffling window size, and activation functions on prediction irreproducibility, even under very controlled synthetic data. While, as one would expect, randomness in initialization and in shuffling the training examples exacerbates the phenomenon, we show that model complexity and the choice of nonlinearity also play significant roles in making deep models irreproducible.

Low Complexity Approximate Bayesian Logistic Regression for Sparse Online Learning

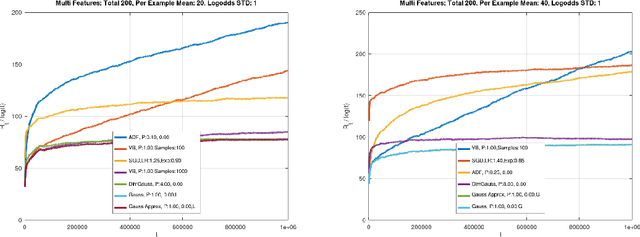
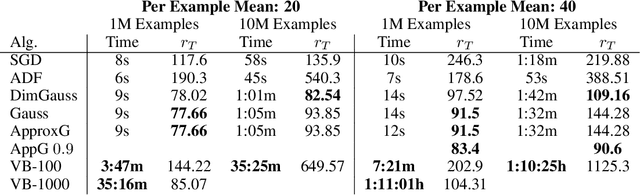
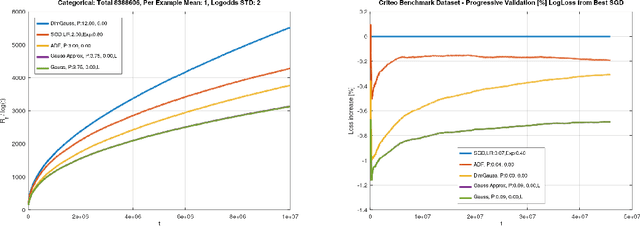
Theoretical results show that Bayesian methods can achieve lower bounds on regret for online logistic regression. In practice, however, such techniques may not be feasible especially for very large feature sets. Various approximations that, for huge sparse feature sets, diminish the theoretical advantages, must be used. Often, they apply stochastic gradient methods with hyper-parameters that must be tuned on some surrogate loss, defeating theoretical advantages of Bayesian methods. The surrogate loss, defined to approximate the mixture, requires techniques as Monte Carlo sampling, increasing computations per example. We propose low complexity analytical approximations for sparse online logistic and probit regressions. Unlike variational inference and other methods, our methods use analytical closed forms, substantially lowering computations. Unlike dense solutions, as Gaussian Mixtures, our methods allow for sparse problems with huge feature sets without increasing complexity. With the analytical closed forms, there is also no need for applying stochastic gradient methods on surrogate losses, and for tuning and balancing learning and regularization hyper-parameters. Empirical results top the performance of the more computationally involved methods. Like such methods, our methods still reveal per feature and per example uncertainty measures.

Smooth activations and reproducibility in deep networks

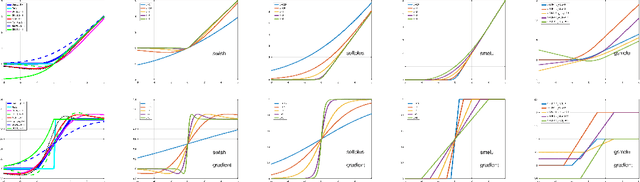
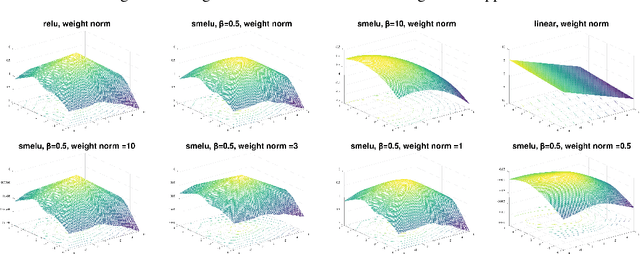
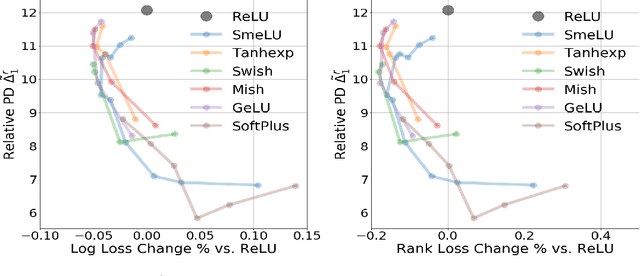
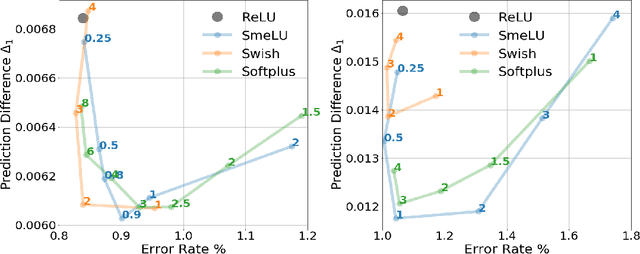
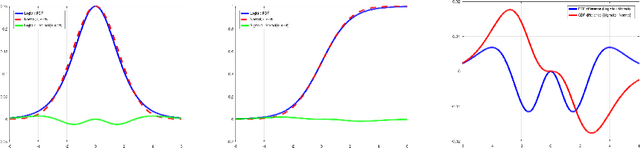
Deep networks are gradually penetrating almost every domain in our lives due to their amazing success. However, with substantive performance accuracy improvements comes the price of \emph{irreproducibility}. Two identical models, trained on the exact same training dataset may exhibit large differences in predictions on individual examples even when average accuracy is similar, especially when trained on highly distributed parallel systems. The popular Rectified Linear Unit (ReLU) activation has been key to recent success of deep networks. We demonstrate, however, that ReLU is also a catalyzer to irreproducibility in deep networks. We show that not only can activations smoother than ReLU provide better accuracy, but they can also provide better accuracy-reproducibility tradeoffs. We propose a new family of activations; Smooth ReLU (\emph{SmeLU}), designed to give such better tradeoffs, while also keeping the mathematical expression simple, and thus training speed fast and implementation cheap. SmeLU is monotonic, mimics ReLU, while providing continuous gradients, yielding better reproducibility. We generalize SmeLU to give even more flexibility and then demonstrate that SmeLU and its generalized form are special cases of a more general methodology of REctified Smooth Continuous Unit (RESCU) activations. Empirical results demonstrate the superior accuracy-reproducibility tradeoffs with smooth activations, SmeLU in particular.

Anti-Distillation: Improving reproducibility of deep networks

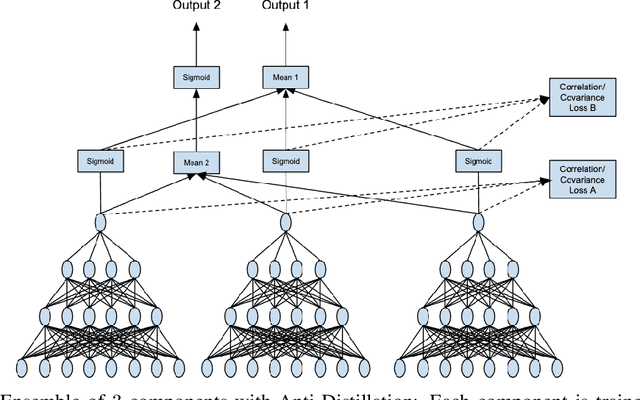
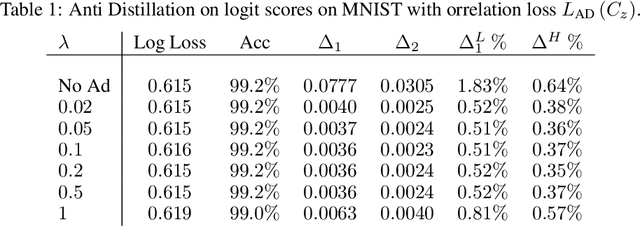
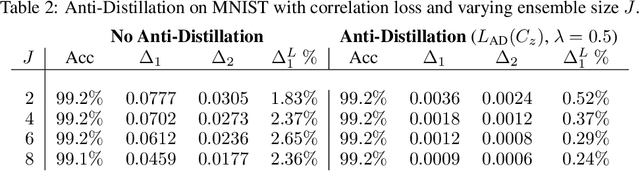
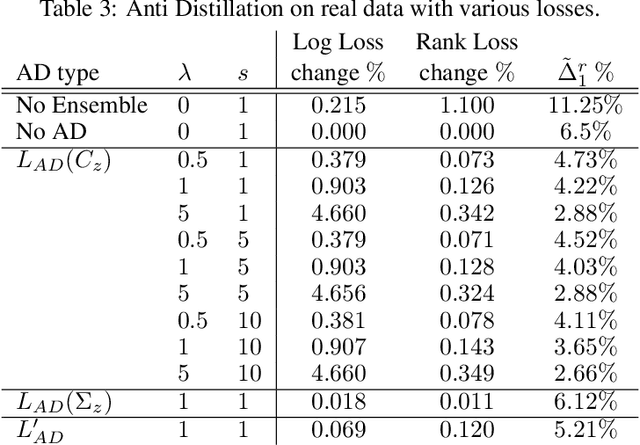
Deep networks have been revolutionary in improving performance of machine learning and artificial intelligence systems. Their high prediction accuracy, however, comes at a price of \emph{model irreproducibility\/} in very high levels that do not occur with classical linear models. Two models, even if they are supposedly identical, with identical architecture and identical trained parameter sets, and that are trained on the same set of training examples, while possibly providing identical average prediction accuracies, may predict very differently on individual, previously unseen, examples. \emph{Prediction differences\/} may be as large as the order of magnitude of the predictions themselves. Ensembles have been shown to somewhat mitigate this behavior, but without an extra push, may not be utilizing their full potential. In this work, a novel approach, \emph{Anti-Distillation\/}, is proposed to address irreproducibility in deep networks, where ensemble models are used to generate predictions. Anti-Distillation forces ensemble components away from one another by techniques like de-correlating their outputs over mini-batches of examples, forcing them to become even more different and more diverse. Doing so enhances the benefit of ensembles, making the final predictions more reproducible. Empirical results demonstrate substantial prediction difference reductions achieved by Anti-Distillation on benchmark and real datasets.

Logistic Regression Regret: What's the Catch?

We address the problem of the achievable regret rates with online logistic regression. We derive lower bounds with logarithmic regret under $L_1$, $L_2$, and $L_\infty$ constraints on the parameter values. The bounds are dominated by $d/2 \log T$, where $T$ is the horizon and $d$ is the dimensionality of the parameter space. We show their achievability for $d=o(T^{1/3})$ in all these cases with Bayesian methods, that achieve them up to a $d/2 \log d$ term. Interesting different behaviors are shown for larger dimensionality. Specifically, on the negative side, if $d = \Omega(\sqrt{T})$, any algorithm is guaranteed regret of $\Omega(d \log T)$ (greater than $\Omega(\sqrt{T})$) under $L_\infty$ constraints on the parameters (and the example features). On the positive side, under $L_1$ constraints on the parameters, there exist algorithms that can achieve regret that is sub-linear in $d$ for the asymptotically larger values of $d$. For $L_2$ constraints, it is shown that for large enough $d$, the regret remains linear in $d$ but no longer logarithmic in $T$. Adapting the redundancy-capacity theorem from information theory, we demonstrate a principled methodology based on grids of parameters to derive lower bounds. Grids are also utilized to derive some upper bounds. Our results strengthen results by Kakade and Ng (2005) and Foster et al. (2018) for upper bounds for this problem, introduce novel lower bounds, and adapt a methodology that can be used to obtain such bounds for other related problems. They also give a novel characterization of the asymptotic behavior when the dimension of the parameter space is allowed to grow with $T$. They additionally establish connections to the information theory literature, demonstrating that the actual regret for logistic regression depends on the richness of the parameter class, where even within this problem, richer classes lead to greater regret.